基于统计最优的近场声全息理论与仿真实验❋

刘 凯，张春良，岳 夏

（1.南华大学 机械工程学院，湖南 衡阳 421001；2.广州大学 机械与电气工程学院，广东 广州 510006）

0 引言

近场声全息作为一种功能强大的噪声源识别以及声场可视化工具，通过测量声源的近场声压信息，能够重建声源表面以及整个三维声场中的各声学量，对噪声源的有效控制和声辐射特性的研究具有重要的意义。基于空间傅里叶变换的平面近场声全息（FFT-based planar NAH）技术是解决声学问题的一种快速有效的方法［1-3］。但当遇到大型声源时它就有一定的缺点，由于测量点较多，测量难度加大，测量时间和成本也就增加。针对上述情况2003年Williams提出了局部近场声全息技术（Patch-NAH），利用求平面波、倏逝波的叠加系数来重建声场的统计最优平面近场声全息技术（SOPNA H）就是其中的一种。因其不存在卷积运算从而避免了FFT-based planar NA H中存在的问题［4］。

1 统计最优平面近场声全息原理

根据基于空间傅里叶变换的平面近场声全息的基本理论可知：自由声场为z＞0的正半空间，z＜0的负半空间为声源位置，在z＞0近场范围内的任何平面上的声压可以看成是无数个空间波数域的平面传播波和倏逝波的叠加［5］。假设空间声场中任意点（x，y，z）处的复声压为p（r）＝p（x，y，z），f为其频率，声波在空气中的传播速度为c0，k＝2πf／c0为声波数，测量面与声源的距离为d。声源与测量面的示意图见图1。

复声压p（r）的理论公式为：

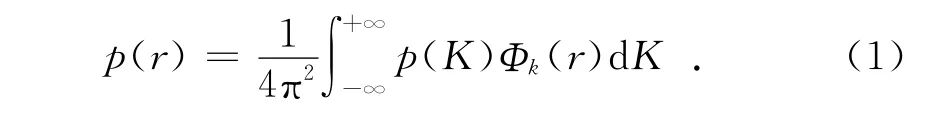
其中：K＝（k x，k y）为波数矢量，k x，k y分别为x，y方向上的空间波数；p（K）为平面声压角谱；当时，z方 向 上 的 空 间 波 数Φk（r）为 平 面 传 播 波，当时，k z＝为平面倏逝波，Φk（x，y，z）＝为空间波数域的单元平面波。

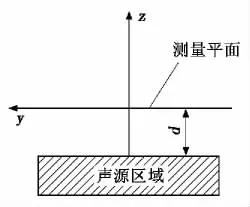
图1 声源与测量面示意图

SOPNA H的核心内容为：令p（r hn）为全息面h上第n个测量点r hn＝（x n，y n，z n）处的复声压（假定全息面上均布N个测量点），而p（r）为0≤z≤z h面上任意重建点r＝（x，y，z）处的复声压，则有：

其中：c n（r）为权重系数。根据波场叠加原理可知，相波同数矢量的单元平面波具有可叠加性，则有：

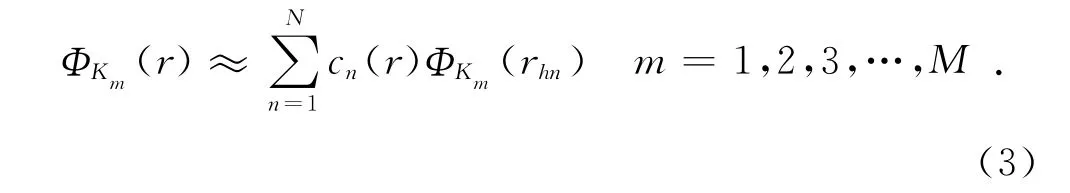
其中：M为空间波数平面上的网格节点数；ΦKm（r）和ΦKm（r hn）由Green函数确定。令：

则式（3）确定的M（M≥N）个线性方程所构成的线性方程组表示成矩阵的形式为：

则式（7）的正则化解为：

其中：AT为矩阵A的共轭转置矩阵；I为单位对角矩阵；θ为起滤波作用的正则化参数。一定条件下，正则化参数的公式为：

其中：S NR为包含随机误差和噪声的信噪比。

将式（8）代入式（2）中可得：

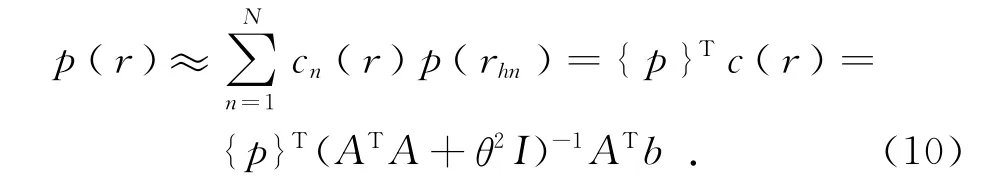
其中：｛p｝T＝［p（r h1），p（r h2），…，p（r h N）］为｛p｝的转置，｛p｝为全息面h上测量得到的声压值。

2 正则化研究

对于方程Ax＝b，其正问题是由已知的A和x求解b，而由已知A和b求解x为反问题。求解反问题的稳定近似解的方法之一是正则化方法，它由Tikhonov和Phillips在20世纪60年代初提出。正则化方法的目的是要滤掉或者减弱奇异值项对解的影响。本文介绍一种特别有效的正则化处理方法，即Tikhonov正则化方法。选择合适的范数来度量使得解比较平滑，通过在求解不适定性问题时附加一限制条件来压制右端误差影响。即：

其中：λ为正则化参数；Ω（x）为平滑范数。残余范数和解的“大小”之间的平衡由λ控制。当λ＝0时，式（11退化为一最小二乘问题，解未经正则化。为了求解式（11），取Ω（x）＝‖Lx‖2为平滑范数，L为实正则化矩阵，其维数为p×n，通常p≤n，则式（11）变为：

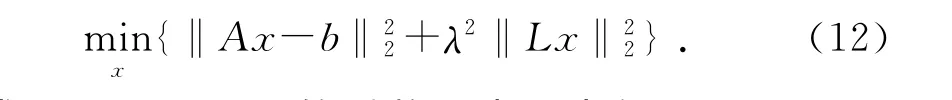
式Ax＝b展开项的系数可表示为如下Tikhonov问题：

式（13）的解为：

如何选择Tikhonov方法中的λ是正则化方法的主要问题，假设λ过大，则会求得过正则化解；假设λ过小，则会求得欠正则化解。这就需要寻找一最适的正则化参数，通常由L曲线准则法［6］和Tikhonov的先验估计法来选取λ。本文选择正则化参数时采用L曲线准则法（即以log-log尺度来描述‖Ax-b‖2和‖Lx‖2的曲线对比，曲线形状通常呈L状，故称为L曲线准则），λ通常选在L曲线的拐角处。λ选取过大时即选在了拐角的右侧，得到的解由于失去了大量的高空间频率信息而显得过于平滑，正则化的解仅由奇异值很大的很少几项构成；λ选取过小时即选在了拐角的左侧，正则化后的解包含了一些对于测量误差非常敏感的奇异值很小的项。

3 声全息数值仿真

3.1 点声源仿真设置

选取一对点声源进行数值仿真，这一对点声源具有同样的声源特性，在自由场条件下假设：声速c0＝340 m／s，空气密度ρ0＝1.293 kg／m3，频率f＝1 500 Hz，两点源之间的距离为0.8 m，源半径r＝0.001 m。声源表面法向振速v＝2.5 m／s。仿真用的测量阵列为1.4 m×1.4 m，等间距0.1 m布置15×15个传声器。测量距离为0.1 m，重建距离为0.05 m；重建网格与测量网格一样，仿真过程中的信噪比为40 d B。声源、测量面、重建面和阵列布置情况如图2所示。

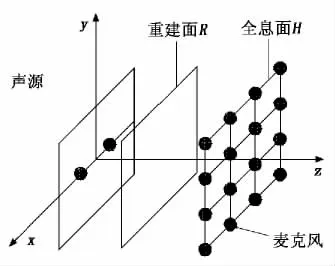
图2 声场重建示意图

3.2 仿真结果

图3是仿真实验中全息面上的测量声压，从图3中可以看出在位置（-0.4，0，0）和（0.4，0，0）各存在一个声源，表明全息面上测量得到的声压幅值符合声场设定的分布。从图3中能对振动体的大概空间位置和振动体个数作出判断，但测量的分辨率还有待提高。

图4为重建面声压幅值图。从图4可以很直观地识别出振动体的个数和空间位置。比较图4（a）、图4（b）与图4（c）可知，在噪声源识别中，结合Tikhonov正则化方法的SOPNAH比FFT-based planar NAH具有较高的精度。

图3 测量声压的等高线图

图4 重建面声压幅值图

4 结论

统计最优平面近场声全息不受有限测量孔径的影响，可以准确实现局部声场的重建。在测量孔径的面积受到限制的条件下，其要求的最小测量孔径实际上要比基于空间傅里叶变换的平面近场声全息小，可以更好地实现噪声源的定位及其辐射声场的可视化。同时为了消除病态性和测量误差的影响，采用了Tikhonov方法进行正则化滤波。通过仿真算例验证了统计最优平面近场声全息是一种稳定且适用性强的声场重建算法，为近场声全息技术应用于实际打下了基础。

［1］王健.封闭空间内近场声全息变换算法及实现研究［D］.西安：西北工业大学，2007：23-35.

［2］于飞，陈剑，周广林，等.噪声源识别的近场声全息方法和数值仿真分析［J］.振动工程学报，2003（3）：85-89.

［3］李卫兵，陈剑，于飞，等.统计最优平面近场声全息原理与声场分离技术［J］.物理学报，2005（3）：1253-1260.

［4］李卫兵，陈剑，于飞，等.统计最优平面近场声全息对振动体的定位研究［J］.农业机械学报，2005（3）：101-104.

［5］薛玮飞，刘晓明，张智，等.空调器噪声源可视化识别的统计最优近场声全息法及其操作方法：中国，CN101556187［P］.2009-10-14.

［6］陈达亮，舒歌群，卫海桥.近场声全息正则化方法比较［J］.天津大学学报，2008（6）：696-702.