基于加工能耗最小的相贯线割炬角优化算法研究

谭 肖

（湘潭大学 信息工程学院，湖南 湘潭 411105）

0 引言

相贯线切割广泛应用于桥梁、建筑、钢结构等产业，但其加工精度还有很大的进步空间。通过对相贯线切割建立数学模型并优化、对加工设备不断提升和更新换代以及数控加工的引入，使得相贯线加工的精度有了很大的进步，从原来的粗糙型手工加工发展到现在的较精密型数控加工［1，2］。

在实际加工中，割炬角角度的不同导致刀具与加工平面的接触角度、面积以及加工力矩不同，相应地在加工切割时刀具的阻力不同，对割炬角进行优化，可以减小刀具阻力、降低能量消耗，具有一定的工程意义和价值［3，4］。目前针对割炬角计算算法的研究已经较为深入，对割炬角的具体计算取得了一定的成果，并运用到了实际中［5，6］，但就能量消耗这一方面却涉猎不多，缺乏对割炬角的优化算法，生产成本没有得到有效的控制。为此，本文提出了一种基于加工能耗最小的割炬角优化算法。该算法通过建立加工切割中包括加工刀具碰撞回避条件、轨迹加工精度条件、轨迹加工限制等加工轨迹限定条件数学模型，确定能量消耗目标函数，通过计算得到能耗最小的割炬角角度。

1 加工轨迹限定条件

相贯线加工示意图如图1所示，令θg（g＝1，2，3，…，n）为加工刀具在相贯线上某点对应的割炬角，L为加工刀具的长度，两圆管的半径分别为Rt和R s，轴线方向分别为Y轴方向、Z轴方向。以割炬角为参数，相贯线上M点可表示为：

加工过程中应满足以下条件：

（1）刀具碰撞回避条件：

其中：σ为实际加工中刀具尺寸的安全系数，σ＞1。

（2）相贯线轨迹加工精度条件。设起始加工的割炬角为θ1，结束加工割炬角为θn，将两点之间的加工区段分割为θ＝｛θ1，θ2，θ3，…，θn｝，得到n个离散加工刀具刀心点P M（θm）。设加工中连续两点的角度误差Δθg＝θm-θm-1，则区间连续加工点精度条件为：

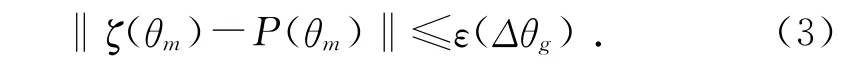
其中：ζ∈f，为加工系统中的一组轴运动映射函数。式（3）表明：位于两加工点间的刀具空间变量所相应的空间坐标与实际加工中位置距离误差不大于ε（Δθg）。

（3）轨迹加工限制。设加工起始割炬角θ1运动到结束割炬角θn的总耗时为T s，加工点区间运行时间为Δt m，有T s刀具与夹具接触点以及加工点上的速度与力矩限定条件为：

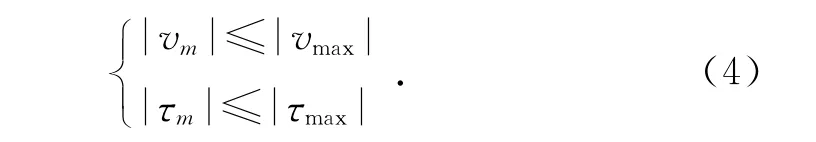
其中：v m为刀具在加工点区间m的进给速度；vmax为最大进给速度；τm为刀具在加工点区间m的输出力矩；tmax为最大输出力矩。

2 能耗最小优化加工路径

对能耗最小建立目标函数：

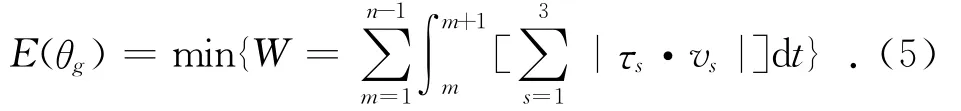
其中：τs为设定的刀具力矩；v s为设定的进给速度。

根据上一节中所述，可以对相贯线能耗最小优化加工路径进行如下描述：①满足刀具碰撞回避条件式（2）；②满足加工规划中的离散点加工精度条件式（3）；③θg在加工范围内，选取合适的轴运动映射函数，在满足连续轨迹点精度条件式（4）的情况下，对加工进行合理的函数值插补；④选择一个合理的时间参数（包括总时间T s以及时间间隔Δt m）。

图1 相贯线加工示意图

3 仿真验证

在优化算法的基础上，将优化算法离散为相应的加工模拟仿真文件，加入到UG加工仿真软件中去，比较优化算法与传统的计算算法得出的割炬角与能耗数据。

（1）在UG中提取的刀轨文件中包含6个参数，前3个参数是刀心点的坐标，后3位参数是刀具的矢量方向，通过后3位参数可以得到传统算法中割炬角的大小，从而计算出力矩τm＝F·sinθg·L（F为刀具的加工力）；同理可以得到按本文提出的算法优化后的割炬角数据。优化前、后割炬角仿真实验对照数据见表1。

表1 优化前、后割炬角仿真实验对照数据表

在加工中刀具的进给速度都是一定的，速度设置见图2。

由表1中的数据可以得到：在保持加工时间不变的条件下，优化后的平均能耗比优化前的平均能耗降低了4.27%（由式（5）可知力矩的大小与能耗成正比）。由此得出结论：优化算法在降低加工能耗方面有着一定的作用。

（2）在加工过程中，除了考虑加工能耗外，还要保证产品的质量，所以对优化前与优化后相贯线坡口切割的轨迹进行对比，见图3。

图2 加工刀具进给速度图

图3 优化前、后相贯线轨迹加工对比图

对仿真轨迹数据进行提取可以得到优化前、后相贯线轨迹对比数据，见表2。

表2 优化前、后相贯线轨迹数据

对比图3以及表2相贯线轨迹数据，可知优化后的轨迹与优化前的轨迹在相贯线轨迹点上的偏差极小，只有0.01～0.03个坐标量，可以忽略不计。由此得出结论，优化算法在降低能耗的同时，能保证相贯线轨迹加工的质量。

4 结论

本文通过建立加工过程的能量消耗目标函数和约束条件，获取优化后的割炬角角度数据；进行模拟仿真得到相贯线的能耗数据与相贯线轨迹数据。在保证相贯线轨迹加工质量的前提下，对整个加工中能量消耗进行优化，降低了能量消耗，减小了加工成本。

［1］Ruiz O， Vanegas C，Cadavid C.Deter mination of intersecting curve bet ween two surfaces of revolution with parallel axes by use of auxiliary planes and auxiliary spheres［J］.The Visual Computer，2011，27（3）：112-115.

［2］Zhang Shuqing，Zhang Junyan.3D object’s intersection analytics：based on stereographic projection ［G］／／International symposium on digital earth 6th.Beijing：［s.n.］，2009：12-14.

［3］苗新刚，汪苏，李晓辉.大构件相贯线焊缝轨迹拟合方法［J］.焊接学报，2011，32（1）：88-93.

［4］Yin Y H，Xie J Y.Reconfigurable manufacturing execution system for pipe cutting ［J］.Enter prise Infor mation Systems，2011，5（3）：168-171.

［5］冯清秀，邹堃.基于 MFC和Open GL的相贯线焊接仿真系统设计［J］.机械设计与制造，2012，32（5）：38-42.

［6］董本志.管件带坡口相贯线数控切割建模与仿真研究［D］.哈尔滨：东北林业大学，2010：40-41.

［7］鄢波，颜国正.基于遗传算法的相贯线扫描机器人轨迹规划［J］.系统工程与电子技术，2005，17（5）：896-899.