3-CRR并联机构动力学分析与仿真

赵进科，陈江义，王少伟

（1.华电郑州机械设计研究院有限公司，河南 郑州 450015；2.郑州大学 机械工程学院，河南 郑州 450001）

0 引言

少自由度并联机构相对于六自由度机构构件少、结构简单、驱动少，各支链之间运动耦合较弱，运动控制方便，构型简单，制造容易，运动正解相对简单，在工业生产及其他领域有着广阔的应用前景［1］。而机构的动力学研究主要包括机构的惯性力计算、受力分析、动力平衡、动力学模型的建立、计算机仿真、计算机动态参数仿真和弹性动力学分析等［2］。其中，动力学模型的建立是诸多动力学问题中一个最重要的方面。3-CRR并联机构是一种具有3个方向移动自由度的并联机构，动力学分析在其机构性能分析中是极为重要的。

Solid Works软件提供了一系列的三维设计产品，帮助设计师减少设计时间，增加精确性，提高设计的创新性。Cos mos Motion作为Solid Works软件的一个插件，其主要功能是对机械系统进行仿真分析［3］。Cos mos Motion可以直接对Solid Works中建立的模型进行运动分析，过程简单方便。

1 3-CRR并联机构描述

本文所研究的3-CRR并联机构［4］如图1所示，这一机构由运动平台、基座和3个支链连接而成。3个支链两两正交，每个支链由1个圆柱副、2个转动副和2个杆件组成，且转动副轴线和圆柱副轴线平行。

为设计和计算方便，用轴线重合的移动副和转动副来代替圆柱副，并且将3个支链的杆件设计为相同，机构的结构参数如表1所示。

表1为机构的结构参数，其中，d0i为导轨i到原点的距离，△d i为导轨i的长度，（e x，e y）为广义坐标系中导轨Z与XY平面的交点坐标，l1，l2和l3分别为3个支链杆件的长度，m1和m2分别为杆1和杆2的质量，mp为导轨上滑块与运动平台的质量和，G1和G2分别为杆件坐标系中杆1和杆2的质心的位置，I13和I23分别为杆件坐标系中杆1和杆2绕质心的转动惯量。

图1 3-CRR并联机构示意图

表1 机构的结构参数

2 动力学方程

在动力学分析中，把移动副作为驱动关节，所有转动副作为从动关节，不考虑运动副中的摩擦力，把所有杆件视为刚性杆。图2为第i支链的动力学分析图，i＝x，y，z。

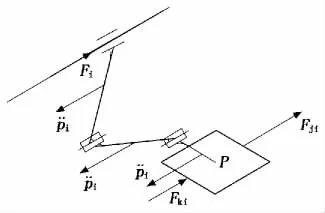
图2 i支链的动力学

当支链i沿i方向移动时，i支链和运动平台可以看作是一个刚体，它们之间并没有相对运动。所以根据达朗贝尔原理，参考图2可以得到：

其中：F i为i支链上滑块的驱动力为运动平台在i方向上的加速度；F ji和F ki分别为沿i方向移动时，j和k支链产生的耦合力；mpi为支链i运动平台和滑块的总质量；mi为支链i两连杆的质量和。

图3为支链j中的2R串联机构。

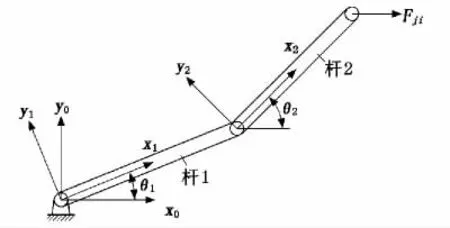
图3 2R串联机构

支链j产生的耦合力F ji可以由虚功原理得到：

其中：J ji＝为支链j串联机构的雅可比矩阵；τj＝为支链j的关节力矢量，它可以利用牛顿-欧拉算法［5］由2R串联机构的动力学分析得到：

根据机构的几何关系，可以计算出各支链2R机构各转角与运动平台输出位移的关系：

将式（5）和式（6）代入式（4）计算出耦合力，然后将耦合力计算结果代入式（1）～式（3）就可得到3-CRR并联机构的动力学方程。

3 动力学仿真

在Solid Works软件中建立3-CRR机构的简单三维模型，并在Cos mos Motion模块中建立并联机构的运动副，得到机构的运动仿真模型如图4所示。

由机构的运动学分析［6］可以得到机构的输入和输出是同步的。所以为3个方向上的滑块添加如下的驱动方程：

仿真时间设置为2 s，在Cosmos Motion中完成此动作的仿真，在仿真结果中测量机构完成此动作所需要的驱动力；按照上述的动力学方程，利用MATLAB程序也可以在给定运动方程时计算出机构在各个方向上需要的驱动力。图5分别为3个方向上的驱动力仿真结果和计算结果。

图4 机构的仿真模型

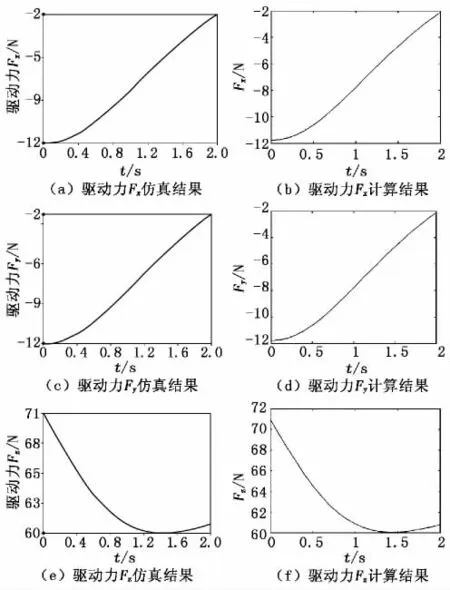
图5 驱动力的仿真和计算结果

由图5可以发现，仿真结果与计算结果基本一致，证明了机构动力学方程的正确性，同时也说明了仿真模型的准确性。

4 结论

以支链动力学为基础，计算各支链之间的耦合力，进而推导出机构的动力学方程。使用Solid Works软件的Cos mos Motion模块对机构进行动力学仿真分析。给定运动轨迹方程，测得所需驱动力，与动力学方程的计算结果相一致。说明动力学方程的正确性，同时也能说明利用Cos mos Motion进行仿真的有效性。

［1］杨斌久，蔡光起，罗继曼，等.少自由度并联机器人的研究现状［J］.机床与液压，2006（5）：302-502.

［2］冯志友，李永刚，张策，等.并联机器人机构运动与动力学分析研究现状及展望［J］.中国机械工程，2006，17（9）：979-982.

［3］马宁.一种新型3-RPUR并联机构的运动学分析及仿真研究［D］.秦皇岛：燕山大学，2007：60-66.

［4］Han Sung Ki m，Lung-Wen Tsai.Design optimization of a cartesian parallel manipulator［J］.Journal of Mechanical Design，2003，125：43-50.

［5］熊有伦.机器人学［M］.北京：机械工业出版社，1993.

［6］Yen Ping-Lang，Lai Chi-Chung.Dynamic modeling and control of a 3-DOF cartesian parallel manipulator ［J］.Mechatronics，2009，19（3）：390-398.