起重机减摆系统装置研究
2014-10-22郭一卓蔺素宏
郭一卓,蔺素宏,蒋 权
(太原科技大学 机械工程学院,山西 太原 030024)
0 引言
起重机小车和吊具由挠性构件钢丝绳来连接。由于这种柔性连接,在小车或大车独立或同时运行时,吊载将在运动空间中产生摇摆,其作业过程过于依赖操作人员的技术水平,自动化程度相对较低,无法满足市场高效率、高精度的需求[1]。
国外学者在起重机的防摆控制上研究比较活跃,Butler H和Honder d G等[2]将自适应控制方法应用于起重机防摆控制上,极大地增强了该系统的鲁棒性;Corrigan G等[3]建立了考虑钢丝绳长度变化的起重机时变模型,同时使用Lyapunov理论对控制系统进行了稳定性分析和仿真试验;Nowacki Z等[4]设计了一个起重机的模糊控制器,不依赖精确的数学模型;Mahfouf M等[5]建立了一种近似线性化的起重机动力学模型,设计了二自由度的ANN控制器;波兰Ah mad M A等[6]提出了门式起重机的滑模控制方法并进行了试验研究。但这些控制方法性能的好坏都不同程度地依赖于所建立的起重机数学模型和所选择的控制系统的状态向量,对于具有高度非线性耦合的起重机控制系统难以取得良好的控制效果。
笔者应用Lagrange力学分析方法对起重机的小车吊载系统建立动态数学模型,试图探讨小车吊载摇摆运动规律及抑制摇摆的方法,并通过simulink进行仿真验证。在此基础上,实际开发了一套定位防摆控制系统。
1 起重机小车吊载系统动态模型分析
1.1 简化模型的建立
起重机小车吊载系统是一个典型的多变量耦合非线性系统。本文的研究中,在满足工程要求的基础上,对系统的特征和建模进行以下合理的简化:①忽略小车电机和减速器等传动机构的非线性影响;②忽略空气阻尼和风载荷阻力的影响;③忽略钢丝绳的长度变化;④忽略钢丝绳与小车连接处的摩擦;⑤不计钢丝绳的自重。
起重机的运动简化模型如图1所示,将起重机的小车、吊载以及连接钢丝绳看成一个移动单摆系统。

图1 小车与吊载运动简化模型
定义小车停止位置为坐标原点O,设定起重机主梁轨道方向(小车向前方向)为x正方向,垂直于主梁轨道方向为y正方向。设小车运行到(d,0)位置的瞬时,吊载的位置为(x,y),吊载的摆角(吊载和钢丝绳的夹角)为θ(弧度);绳长为l(m),吊载质量为m(kg),小车受到的驱动力为F,小车在轨道上运行时所受的摩擦力为f。
根据坐标定义,可得到小车的水平和垂直位移分量:

依据钢丝绳绳长l与吊载摆角θ的关系,则吊载的水平和垂直位移分量为:

通过对式(2)求导可得到吊载在x,y方向上的速度分量。不妨设v t=为小车的速度,为小车的加速度,那么吊载的水平和垂直速度分量可记为:

1.2 基于Lagrange力学分析方法的数学模型
吊载动能T为:

将式(3)代入式(4),经整理得:

以主梁轨道平面作为零势能参考平面,设吊载质点静止位于垂直方向时,距零势能面的距离为h,则吊载势能为:

广义坐标下实际的拉格朗日函数L=T-U[7],代入相关参数经整理得:

在实际情况下,吊载摇摆角度θ一般在±10°以内,因此取cosθ≈1,sinθ≈θ,得小车吊载动态模型为:

当绳长不变时,即l·=0,小车吊载动态模型可进一步简化为:

从式(9)中可得到如下结论:①吊载摆角与小车运行加速度及绳长有关,与吊载的质量无关;②小车在静止或匀速运行时,吊载自身将呈现单摆运动特性,小车在进行加减速运动时,会对吊载摆角产生影响;③在吊载的摆动周期T p内,对小车施加恒定的加减速度后,吊载将回到初始状态,如果初始状态时吊载无摇摆,那么加减速结束后吊载将保持无摇摆状态。
2 simulink仿真验证
根据上述建立的数学模型,在 MATLAB/simulink环境中建立起重机的小车吊载模型,并对小车运动对吊载摆角的影响进行仿真分析[8,9]。图2为起重机控制系统的simulink仿真模型。图3和图4分别为小车下摆角的位置响应和小车位置响应。角度响应进行了仿真(由于篇幅所限此处未给出仿真结果图)。仿真结果表明,当负载质量与绳长两个可变参数在规定的参数变化范围内时,系统控制的动态性能满足我们的设计要求,即系统灵敏度变化不超过5%。
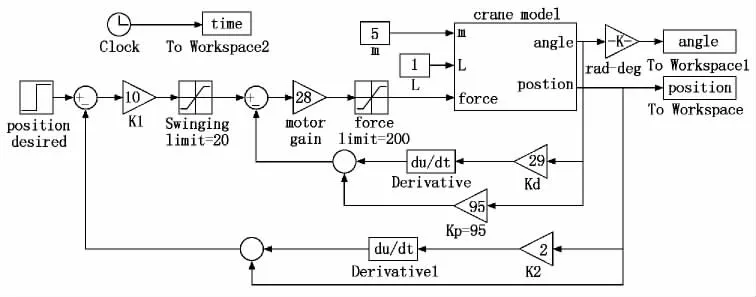
图2 起重机控制系统的simulink仿真模型
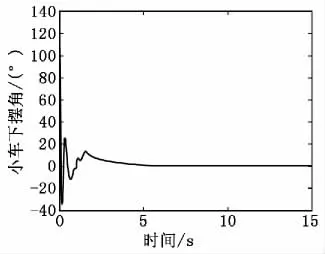
图3 小车下摆角的位置响应
由图3和图4可以看出此仿真控制系统的鲁棒性较好,小车的位置和小车的下摆角在10 s内都能达到稳定。
本文对不同负载质量及不同绳长时小车的位置和

图4 小车位置响应
3 起重机小车吊载系统平台的搭建与硬件配置
在模型分析和MATLAB/Simulink仿真验证的基础上,本课题组实际开发出了一套定位防摆控制系统装置,见图5。

图5 定位防摆控制系统装置
吊载系统的整套机械部件安装在起重机模型的梁和小车上。导轨固定在主梁上,皮带轮、AC伺服电机固定在端梁上,使用AC伺服电机集成的光电增量式编码器间接测量小车的位移。STM32控制器、实时反馈运行状态的陀螺仪、AC伺服电机及驱动器、桥式吊载装置通过机械或电气手段连接成一个整体。
ST M32控制器是定位防摆控制系统的核心,该控制器具有高效可靠、低功耗、接口丰富、运算速度快等优点。吊具摆角实时监测系统是定位防摆系统的重要组成部分,该系统的传感器为陀螺仪,其实时采集系统的吊载摆角、速度信息,以便控制器对小车进行控制。该装置检测的吊载摆角范围可达±35°,精度为2 000°/s,检测频率为200 Hz,陀螺仪通过SPI通信方式与定位防摆自动控制系统进行数据交换。
4 起重机小车吊载系统的控制过程
利用起重机的定位防摆控制系统,在小车运行过程中,根据小车速度和位移的规划,通过小车吊载模型计算得到吊载加速度;通过陀螺仪的实时检测并反馈摆角,计算吊载实际加速度。对两者的差别进行PI调节,并将调节值叠加到给定的小车速度中,这样当采用类正弦加速模式驱动小车,能够使吊载在小车停止后回到初始状态。
试验测试证明该起重机定位防摆系统可在小车运行停止阶段,吊载4个摆动循环内将吊载摆角控制在0.5°之内。对于桥式起重机,吊载在接近地面处,摆幅可控制在±300 mm之内。
5 结论
本文对起重机小车吊载定位防摆问题进行了系统的研究,并实际开发搭建了起重机小车吊载的定位防摆控制系统,通过STM32控制器实现了小车吊载定位防摆的自动控制。实际应用表明该系统具有以下特点:能有效防止吊载摇摆,且保持小车平稳运行,减轻了起重机司机的工作强度;实现了小车快速运行且精准定位,提高了起重机作业效率,为设备自动化、智能化奠定了坚实的基础;装置硬件配置灵活,安装简单,系统可靠,故可广泛应用于有效率需求的起重设备上。
[1]Benhidjeb A,Gissinger G L.Fuzzy control of an overhead crane perfor mance comparision with classic control[J].Control Engineering Practice,1995,3(12):1687-1696.
[2]Butler H,Honderd G,van Amerongen J.Model reference adaptive control of a gantry crane scale model[J].IEEE Control Systems,1991,11(1):57-62.
[3]Corrigan G,Giua A.An implicit gain-scheduling controller for cranes[J].IEEE Transactions on Control Systems Technology,1998,6(1):15-22.
[4]Nowacki Z.On the robustness of fuzzy control of an overhead crane[G]//Proceedings of the IEEE International Sy mposium on Industrial Electronice.[s.l.]:IEEE,1996:433-437.
[5]Mahfouf M,Kee C H,Abbod M F,et al.Fuzzy logic-based anti-sway control design for overhead cranes[J].Neural Computing & Applications,2000,9(1):38-43.
[6]Ah mad M A,Nasir A N K,Ishak H.Techniques of anti-sway and input tracking control of a gantry crane system[G]//Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation.Changchun:IEEE,2009:262-267.
[7]张则强,程文明,钟斌,等.起重机集装箱二自由度摆角模型与仿真[J].西南交通大学学报,2006,41(6):697-698.
[8]王金诺,程文明,张质文,等.起重机刚性减摆系统的动态仿真[J].铁道学报,1995,17(1):34-40.
[9]郭立观.港口起重机智能定位防摆系统研究与仿真[D].太原:太原科技大学,2009:21-23.
