基础沉降及地震作用对桥梁行驶磁悬浮列车的安全性影响

李青良 秦煜

摘要：本文對基础沉降和地震作用下多跨桥梁行驶磁悬浮列车的安全性进行了研究。在三维非线性有限元分析中考虑导轨不平顺、恒定增益调整的比例积分（PI）控制、磁悬浮导轨与桥梁的相互作用。通过数值分析得出基础沉降下列车速度对悬浮间隙稍有影响，但是地震作用下列车速度对间隙基本无影响。当初始横向和竖向电磁力的比值（ ）增大时，磁悬浮能抵抗更大的地震作用。对于间隙为1cm、承受均匀力的情况，当 时，有限元分析结果表明两墩的极限竖向沉降差值可达3cm，横极限向挠度差值可达2.2cm。地震荷载作用下，当 时，间隙为10cm，最大横向加速度可达410 。通过对以上情况分析，可得出电磁悬浮系统（EMS）可以抵抗基础沉降，电动悬浮系统（EDS）可以同时抵抗基础沉降和地震作用。

关键词：地震动；有限单元法；基础沉降；磁悬浮列车；比例积分（PI）控制；导轨不平顺

1. 引言

由于磁悬浮列车具有耗能低、噪音小，与传统车轮列车相比安全性更高等优点，所以它的使用越来越广泛。此外，不难相信磁悬浮列车的速度最终可达到500 。对于磁悬浮列车，桥梁结构是最合适的，但是会发生基础沉降和地震作用，所以磁悬浮列车、导轨和桥梁之间的相互作用成为从安全性考虑最重要的问题。可以采用有限单元法对它的动力性能进行模拟分析。

例如，Song和Fujino（2008年）建立了三维模型对磁悬浮列车和桥梁的相互作用进行了研究，在研究中采用多种改进的有限元模型模拟结构构件。Yang和yau（2011年）采用交互迭代的方法分析磁悬浮列车在高架导轨上行驶时的动力响应。Duan等人（2011年）对磁悬浮交通平台的大行程线形运动进行了发展，并采用有限元分析对电磁解耦空间分布的设计方法进行了优化。Ju等人（2012年）采用有限元方法对磁悬浮列车-桥梁-土间的相互作用进行了全方位模拟，在研究中，采用行驶在Timoshenko梁上的列车分析结果对有限元模型进行了验证。

已经有两个研究对相关的地震响应进行了分析。Yan（2010年）研究证实，当受控制的磁悬浮列车行驶的悬浮导轨由于水平地震作用发生摇动时，出于安全原因，设置的混合控制器将在规定的稳定范围内对悬浮间隙进行调整，并且能够降低列车的加速度相应，提高行驶质量。Pan等人（2010年）通过基于水平震动平台的地震波传播仿真，对磁悬浮系统的动力响应和磁悬浮力进行了研究。他们得出结论横向稳定和悬浮性能与共振频率5Hz下的激励幅值和激励频率相关。

很多研究对基础沉降和导轨不平顺进行了研究。Yau（2009年）研究表明悬浮间隙的增大可能会增强列车的响应，但是对于高速行驶的列车，具有很小间隙，一旦在导梁支座处发生地面沉降，列车响应的扩大会很明显。Lee等人（2009年）发现列车间隙虽然不受跨长和导轨结构的阻尼比影响，但是受列车速度、摩阻系数，以及导轨变形率影响特别大。Kong等人（2011年）针对行驶在弹性导轨上的磁悬浮列车的动力特性分析建立了计算模型，模型是考虑导轨不平顺下的五自由度模型。Ren等人（2010年）同时考虑导轨不平顺和磁悬浮列车，采用仿真软件建立数值模型对磁悬浮系统的动力特性进行分析。Shi等人（2007年）建立了动力模型对高速下电磁悬浮列车和导轨的相互作用进行了模拟分析，同时采用这个模型对不平顺因素的作用进行了分析。Zhao和Zhai（2002年）建立了10自由度模型来分析恒定速度下，行驶在三种类型导轨上的磁悬浮列车。同时，研究也对导轨随机不平顺进行了讨论研究，在模拟分析列车响应和行车舒适度时将此因素也考虑在内。

本文对基础沉降和地震作用下，在多跨简支桥梁上行驶磁悬浮列车的安全性进行了研究。在非线性有限元中对轨道不平顺、车-桥相互作用以及比例积分（PI）控制进行考虑。通过有限元模拟分析，拟可得出考虑基础沉降和地震作用，磁悬浮列车在桥梁高速行驶的安全性能。

2. 磁悬浮列车与桥梁相互作用的有限元分析

磁悬浮系统可以分成两类：（1）EMS系统：通过带有吸引力的电磁力将列车浮起；（2）电动悬浮系统（EDS）：通过超导材料的排斥力将列车浮起。两种系统的间隙完全不同（EMS系统为1cm，EDS系统为10cm）。本文采用有限元分析模型对两种系统的行驶磁悬浮列车与桥梁相互作用进行了分析。

2.1 磁悬浮列车控制系统

电磁力是电路电流大小和电磁体与导轨距离的函数（Shi等人2007年研究；Bittar和Sales等人1998年研究）。

（1）

式中：上标 =当前时间；下标 =第 个磁性车轮， ； =常数因子。变量 为控制电流， 为悬浮间隙高度，计算如下：

（2）

式中： =静力平衡状态下的要求高度； =第 个磁性车轮的竖向位移； =第 个磁性车轮的整体 坐标； =由第 个磁性车轮产生的梁挠度； =轨道不行顺。本文采用的不平顺参数由Au等人（2002年）提出，具体数值见表1。在静力平衡状态，公式（1）初始量：

（3）

式中： =控制电流的要求值； =悬浮间隙的要求高度。荷载 为在竖向（浮起方向）或者横（引导方向）向作用在磁轮上的静力荷载，它等于磁悬浮列车的重力。Lee等人（2006年）指出悬浮和导向两个分离型对高速行驶有利，因为它们相互不干扰。由于本文对高速行驶状态下磁悬浮进行研究，所以应该设置分离型，对悬浮和导向采用同一个控制系统。

表1 本研究中铁轨的不平顺参数

Ju等人采用比例积分、梯形积分法和 方法，获得了磁悬浮系统反馈控制的紧凑方程如下：

（4）

式中： ； ； =磁悬浮线圈初始感应系数； =电路线圈电阻； =比例增益； =积分增益； =两个时间步之间的时间步长度； 。由于在等式（4）的右边只有一个未知数 ，如果知道最新的悬浮高度，可以计算相应的 。然后用 通过公式（1）计算 时间的电磁力 。

2.2 磁悬浮列车的有限元方程

Ju等人（2012年）计算了四个自由度（ ）两节点梁单元竖向（z方向）的车轮等效荷载如下：

（5）

式中： =两节点梁单元z方向移动和y方向转动； =梁单元立方体埃尔米特插值函数。公式（2）的位移计算如下：

（6）

式中： =轮压处的沿z向位移，沿y方向的力和位移可以用相似的方法计算得到。

建立行驶磁悬浮列车的模型包含前轮磁力、弹簧阻尼单元、集中质量和刚度连接，与真实的高速列车相同（Ju等人2006年研究）。对于弹簧阻尼单元，Kelvin-Voigt单元平行的包含弹簧和阻尼，刚度为 何阻尼 。刚度或者阻尼矩阵计算如下：

（7）

式中： =刚度矩阵S的弹簧常数 或者阻尼矩阵S的阻尼常数；上标R和L=分别代表右侧和左侧； =主节点和从属节点的坐标差。

下面给出了标准动力方程：

（8）

式中： ， 和 =是磁懸浮列车与其他单元（例如桥梁和土）的刚度矩阵； =力向量； = 位移向量。这个列车振动的有限元模型已经得到了Ju等人（2012年）的验证。对于基础沉降和地震荷载，之前解动力方程的方法得到了修正，修正后的方法与标准牛顿-拉普森方法结合，不需要额外步骤。

1）如果考虑基础沉降，应进行静力线性有限元分析计算出初始变形，在有限元模型中，在墩底施加一个静力荷载，墩底与具有六个自由度的弹簧连接来模拟基础，因此发生沉降时，基础仍可以发生变形。

2）如果考虑地震荷载作用，弹簧可以用来模拟基础转动的自由度，然后模拟墩底考虑地面加速度的三维地震变形。

3）在每一个时间步中，公式（2）用来计算磁轮间隙，同时公式（1）和（4）用来计算当前磁轮电磁力，公式（5）用来计算磁轮的等效力向量，然后代入公式（8）中的合力 计算。

4）通过解方程（8）可以得到每个牛顿-拉普森迭代中的节点位移。

5）用当前的节点位移再一次计算合力 ，将新得到的合力 代入下一个牛顿-拉普森迭代中。

以上步骤只能修正每个磁轮电磁力迭代的合外力向量 ，在牛顿-拉普森方法中，其他步骤与以上步骤相同。

2.3 对列车-导轨-桥梁和有限元模型的说明

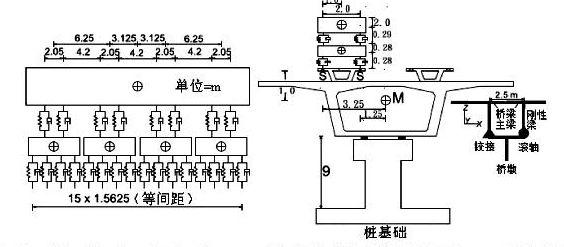
虽然商业用途的磁悬浮列车系统相对较少，由于它具有很大的载客能力，世界上推荐使用此技术的越来越多。因此，将传统高速列车系统与磁悬浮系统对比具有极高的价值，本文分析的磁悬浮列出与在台湾运营的SKS-700高速列车（Ju2012年）非常相似。在x轴方向，磁悬浮列车行驶方向具有12节车厢，z轴负方向为重力方向。Ren等人（2010年）提出了一个共有16个转变力的最合适的列车简化模型，因此本文采用这种模拟方式来模拟列车与导轨间的磁悬浮力。图1是12节车厢的一节车厢和桥梁示意图，每一个车厢具有4个转向架，每一个转向架有4个磁轮。模型采用集中质量单元、弹簧阻尼单元、刚性连接作用以及磁轮荷载概念，用集中质量单元建立模型。在列车和桥之间采用8个空气弹簧模拟，对于二系悬挂采用弹簧阻尼单元模拟。在转向架下面是6个弹性弹簧，作为一系悬挂施加，也可以用弹簧阻尼单元模拟。

图1 磁悬浮列车的几何尺寸，采用弹簧阻尼、刚体和集中质量的模型

（M=梁中心节点；S=磁轮目标节点，作为从属节点由主节点M控制）

本文研究的磁悬浮的二系悬挂和列车质量与Ju（2012年）研究中提到的台湾高速列车相同。每节车厢的质量是38.9t，每个转向架的质量是3t。车厢关于x轴、y轴和z轴的惯性矩分别为97.2，1470.0和1267.5 ，其中转向架关于x轴、y轴和z轴的惯性矩分别为2.47，3.69和3.05 。一系悬挂关于x轴、y轴和z轴的阻尼系数分别为40 ，刚度系数为1200 ，二系悬挂关于x轴、y轴和z轴的阻尼系数分别为2500，60和20 ，刚度系数分别为140，140和330 。

本文研究桥梁是跨径为30m的一系列简支梁桥，墩高为9m，桩基础长60m，墩帽到墩顶间为变截面（图1）。这个桥梁为铁路桥梁，列车最大速度为400 。用两节点梁单元来模拟桥梁主梁和墩，因为频率对这些矩阵的影响不大，本文采用频率为4.8Hz的等效矩阵来模拟桥梁的基础和土，如表2所示。磁轮单元的目标节点作为从属节点布置（图1中的节点S），这个节点由梁节点控制（图1中节点M），在铁轨方向的梁节点平均间距为0.625m。图1中的钢梁用来模拟简支在墩帽上的主梁2.5m的偏心。采用Newmark直接积分法和质量一致的方法分析计算平距加速度，同时采用前提是对称超松弛（SSOR）的，共轭的梯度法（Ju 2010年），其中时间长为0.0005s。

3. 基础沉降作用下桥梁行驶磁悬浮列车的安全性

本部分研究了基础竖向沉降和EMS系统发生转动下，桥梁行驶磁悬浮列车的安全性。由于EMS系统的间隙远远小于EDS系统，因此基础沉降的极限情况从EMS系统分析。

根据Shi等人（2007年）研究可以得出，悬浮系统的参数可以写成如下形式：悬浮间隙（ ），静力平衡状态的电流（ ），电路线圈电阻（ ），比例增益（ ）以及PI控制器的积分增益（ ）分别为0.01m，43A，1 ，0.01和6.0。然后建立由50跨30m简支梁组成的有限元模型，在第20个墩添加基础沉降。车速为120 时，每个磁轮的初始横向荷载为竖向荷载的1/3（ ）。图2是图中点C发生2.5cm沉降情况下，第20个磁轮经过桥墩时的荷载和悬浮间隙长度。考虑导轨不平顺，两跨会有轻微的不平顺，但是仍然很稳定。在磁轮到达发生基础沉降跨（点B到C）之前，荷载接近静力恒定列车自重15.6 ，悬浮间隙长度接近初始值0.01m。当磁轮经过发生基础沉降的桥跨时，首先由于沉降作用（点B到点C），荷载值下降直到悬浮间距减小，然后荷载值上升直到悬浮间距增加（点C到点D）。由于B和D两点的位移的急剧变化，导致B和D点的发生荷载突变。临界情况发生在磁轮在D点时，悬浮间隙达到最小值，当间距值为0时，列车和闸道接触并发生破坏。因此，在接下来的分析中，在整个列车行驶距离内，本文采用最小的悬浮间距长度最为危险指数进行分析，此外，也列出了最大间隙长度的情况作为参考。

图2 （a）荷载；（b）发生2.5cm沉降时，第20个磁轮经过桥梁时的悬浮间隙长度

（桥梁的变形值放大20倍）

图3是基础竖向沉降作用下的最大和最小悬浮间隙变化。由结果可以得出，考虑导轨不平顺的结果和不考虑的性能基本相同，导轨不平顺只对最大竖向悬浮间隙情况又微小影响。同时可以得出两桥墩的基础极限竖向沉降之差为0.03m，以现在的施工技术完全可以解决，如采用深层桩。此外， 的改变对竖向悬浮间隙，不考虑大振动的沿y轴初始间隙对横向导向间隙的影响不明显。出于简化目的，在图中这些结果未表示出来。Ju（2013年）研究了高速列车行驶在与本文相同桥型上的情况，得出车速为350 时的极限竖向基础沉降值为0.065m，这个值相比磁悬浮列车的极限值稍大一些。

图3 竖向沉降值改变时轨道不平顺和桥跨数目对最大和最小悬浮间隙的影响

图4为桥梁基础绕x轴转动产生的相对y轴变形时极端橫向导向间隙。因为初始竖向电磁力 应该等于列车自重，图中只给出了横向电磁力 的变化。在图 4中，沿桥y轴变形产生的值为0的横向间隙，会随着荷载 的增加而增大，当 从1/3增大到1时，桥梁极限变形会从0.013m增大到0.002m。此外，轨道不平顺对此结果的影响不明显，只有当由于桥梁基础绕x轴转动引起的沿y轴变形非常小时，导轨不平顺对于横向导向间距变得非常重要。在桥梁基础绕x轴转动情况下，不会产生竖向悬浮的极限间隙，本文不考虑这部分内容。

图4 由于绕x轴转动产生y轴变形时，导轨不平顺和 对最大最

小横向导向间隙的影响

图5是竖向基础沉降为0.025m并且存在表1中轨道情况下，列车速度改变对最大最小悬浮间隙的影响。模型沿纵向（x）方向的一阶固有频率在图中也有表示。从图5中可以看出，列车速度对竖向悬浮间隙的影响很小，并且当列车速度约为77 时，达到最小值。这是因为桥梁一阶固有频率2.577Hz等于列车在梁跨（ ）上的速度（ ）。在这种情况下，列车经过点C和点D时不同的变形可以达到最大值，如图5所示。因此，磁轮最小的悬浮间隙在如图2（b）中的点D处。由于这种列车振动只能使点C和点D产生的变形不同很小，所以竖向悬浮间隙值的改变也不大。然而，即使初始间隙很小，比如0.01m，这种情况的影响仍然不能忽视。

图5 竖向沉降为0.025m且存在表1中导轨不平顺时，列车速度对

最大最小竖向悬浮间隙的影响

桥梁一阶固有频率（ ）与列车荷载主频（ ）之间发生共振（ ）将会产生很大的振动（Ju和Lin 2008年研究）。如图1所示，因为列车荷载间距相等为1.5625m，间距 应该用来计算该值。高速行驶列车的一阶固有频率往往小于8Hz，因此，引起共振的速度小于12.5 （45 ）。因为如此低速引起的共振现象并不严重，所以有限元模拟中不模拟车-桥共振作用。然而，如果列车荷载布置不是等间距的，则车-桥共振就不能忽略，因为这时 应该取车厢长度，产生共振的列车速度将达到运营速度，300到600 。

4. 地震作用下桥梁行驶磁悬浮列车的安全性

如图6所示，采用的地震动最大地面加速度在x、y、z轴方向分别为95、171和37 ，这个地震力造成了2010年4月台湾高速列车轻微脱轨。脱轨的主要原因是桥梁和地震动之间的共振（参见Ju2012年研究）。因此，本文用此地震力来分析磁悬浮列车抗震性能，可以将车轮列车与磁悬浮列车的极限情况进行对比分析。有限元模型中建立115个跨径为30m的简支梁，列车可以以120 的速度行驶在桥梁上经历25s的地震作用。根据Ju等人（2006年）研究，可以用刚度值来模拟基础和土的转动自由度，然后在墩底用三个转换自由度模拟地震变形，同时施加图6中的地面加速度。

图6 台湾新华站测得的地震时程[在x轴、y轴和z轴的最大地面加速度分别是95、171和37 ；在墩底（如图1）施加x、y和z方向的三个转换自由度模拟地震变形]

本文研究中考虑了导轨不平顺系数、 、初始间隙和连续的桥跨数量。由于很小的初始悬浮和导向间隙，比如对于EMS系统1cm，不能够抵抗合理的地震作用，在数值模拟中将它们设为5和10cm，这样的设置只适合与EDS系统。本文研究中，对于EDS系统采用同图1相同的模型，这个模型中磁轮的间距很小。本文基于Yang和Yau（2011年）研究，悬浮系统的参数选取如下：静力平衡状态的电流（ ）、电路电阻（ ），比例积分控制器中的比例增益（ ）和积分增益（ ）分别为25 、1.5 、0.3和2.73。

图7为初始悬浮间隙和导向间隙为0.05m，列车速度为120 时，不同地面振动作用下，导轨不平顺和 对悬浮和导向间隙的影响，其中从图6中水平轴可得出地震荷载系数。由图7可以看出，导轨不平顺对横向导向间隙和竖向悬浮间隙的减小不大。此外，增大 能够沿y轴承受更大的地面振动，但是沿z轴不可以，因为初始竖向电磁力 不能改变。

图7 （a）横向导轨间隙；（b）竖向悬浮间隙；初始悬浮间隙和导向间隙为0.05m，不同地面振动作用下，导轨不平顺和 对导向和悬浮间隙的影响

当初始间隙从0.05增大到1m时，图8是与之前同样的一种现象，唯一不同的是地面振动的容许百分比可以达到320%，这个值是初始间隙为0.05m时的两倍。

图8 （a）横向导向间隙；（b）竖向悬浮间隙；初始悬浮和导向间隙为0.1m，不同地面振动作用下，导轨不平顺和 对导向和悬浮间隙的影响

图9所示是初始竖向间隙0.05m，存在导轨不平顺，100%地面振动下， 改变对列车间隙的影响。从图中可以看出，当 增大时，横向导向间隙接近初始导向间隙，这意味着列车可以承担更大的地震荷载。同时，竖向间隙发生微小改变时，产生的影响很小。

图9 （a）横向导向间隙；（b）竖向悬浮间隙；初始悬浮和导向间隙为0.05m，考虑导轨不平顺，100%地面振动作用下，荷载比 改变对导向和悬浮间隙的影响

图10所示的是不存在导轨不平顺、地面振动百分比为100%且 时，改变一个连续梁跨径数目对性能的影响。从图中可以看出，由于磁悬浮列车和导轨没有物理接触，所以对横向和竖向间隙都没有影响。这完全不同于传统列车，传统列车受两跨简支梁间隙的影响非常大。

图10 （a）横向导向间隙；（b）竖向悬浮间隙；100%地面振动作用下（初始间隙0.05m，不存在导轨不平顺， ），一个连续梁跨径数目改变对性能的影响

图11所示是地面振动百分比为100%， 且存在表1中的导轨不平顺情况下，列車速度对最大和最小横向导向间隙的影响。从图中可以看出，横向导线间隙的距离几乎完全依赖于列车速度，这完全不同于传统车轮列车，传统列车的脱轨系数与列车速度的关系特别大。由于磁悬浮列车没有直接与导轨接触，所以列出速度对列车与导轨间距离的影响不是很大，这也是磁悬浮列车的一大优势。

图11 100%地面振动作用下（初始间隙0.05m，不存在导轨不平顺， ），列车速度对横向间隙最大最小值的影响

5. 结论

本文采用有限元模型和比例积分控制研究了基础沉降和地震作用下列车-导轨-桥梁之间的相互作用。同时采用有限元模型研究了桥梁行驶磁悬浮列车的安全性。基于分析结果，本文得出以下结论：

1）对于桥梁基础沉降作用，列车速度对竖向悬浮间隙的影响很小，最小值出现在列车速度与桥梁跨径之比（ ）等于桥梁纵向固有频率时，即使初始间隙非常小（小到仅有0.01m），这个情况的影响仍然不能忽略。在发生竖向沉降或绕x轴转动的位置，导轨不平顺对竖向悬浮间隙或者横向导向间隙都无影响，这种情况对地震作用也相同。

2）对于地震动作用，采用很小的悬浮和导向间隙都不合适，所以本文设定初始间隙最小为0.05m。在这种情况下，列车速度对横向导向间隙的影响非常大，这与传统车轮列车完全不同。在车轮列车中，列车速度与脱轨系数有很大关系。连续梁跨径数目和x轴方向地面震动的改变对导向和悬浮间隙没有影响，因为磁悬浮列车和导轨间没有物理接触。同时简支梁的间距对磁悬浮列车无影响，这与传统列车系统完全不同。

3）当横向电磁力与竖向电磁力的初始比值（ ）增大时，横向导向间隙可以承受更大的地震作用，但是对竖向悬浮间隙无影响。因为在平衡时，竖向电磁力等于磁悬浮列车的自重，不会发生改变。当初始比值 增大时，磁悬浮列车能够承受的最大地面震动由竖向悬浮间隙决定。

4）对于间隙为1cm，施加在多跨简支梁上均匀磁悬浮荷载的EMS系统，有限元结果表明两墩间极限竖向基础沉降差值可以达到3cm，当 时极限横向变形可以达到2.2cm，现有施工技术可以避免这些情况发生。EMS系统的初始间隙必须很小（例如1cm），所以无法抵抗常规的地震荷载作用。如果采用具有很小电磁间隙的EDS系统（如图1所示），当间隙为5cm， 时，最大横向地面加速度可以达到205 。当初始间隙由5cm增加到10cm时，最大地面加速度也将加倍。

参考文献

[1] S. H. Ju， C. C. Leong， Y. S. Ho. Safety of Maglev Trains Moving on Bridges Subject to Foundation Settlements and Earthquakes[J]. Journal of Bridge Engineering， 2014， 19（1） ： 91-100.

编译者简介：李青良（1968-），男，高级工程师，1991年毕业于西南交通大学桥梁工程专业，工学学士