利用几何画板绘制椭圆、双曲线、抛物线的统一轨迹

岂振华

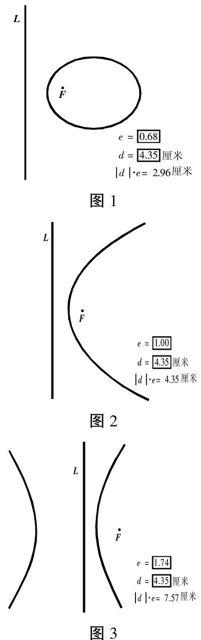
关于椭圆、双曲线、抛物线的统一，在传统教学中，教师告诉学生：“已知点F是平面上的一个定点，L是平面上不过点F的一条定直线，点M到点F的距离和它到直线L的距离之比是一个常数e。当0<；e<；1时，轨迹是椭圆；当e>；1时，轨迹是双曲线；当e=1时，轨迹是抛物线。椭圆、双曲线、抛物线统称为圆锥曲线。”学生被动地接受知识，缺乏对椭圆、双曲线、抛物线统一的直观认识。利用几何画板，学生可以直观地感受到：e从0开始逐渐增大，图形从椭圆变成抛物线，再变成双曲线。椭圆、双曲线、抛物线其实就是一个图形，只不过这个图形的形状随着e的变化而变化而已。本文主要介绍椭圆、双曲线、抛物线统一轨迹的几何画板课件的制作。

单击“绘图”菜单中的“定义坐标系”，在x轴上绘制点F，作点F关于y轴的对称点，过对称点作y轴的平行线L。单击“数据”菜单中的“新建参数”，输入e，单击“確定”。单击“数据”菜单中的“新建参数”，输入d，“单位”选“距离”，单击“确定”。选中参数d，单击“变换”菜单中的“标记距离”。选中直线L，单击“变换”菜单中的“平移”，以标记距离d、固定角度0°，单击“平移”，得到直线L′。改变d的大小，当d>；0时直线L′在直线L的右侧，当d<；0时直线L′在直线L的左侧。选中参数d、e，单击“数据”菜单中的“计算”，输入abs（d）*e，单击“确定”（abs（）是求绝对值的函数）。选中计算结果—d—.e、点F，单击“构造”菜单中的“以圆心和半径画圆”。构造圆和直线L′的交点M1、M2。选中参数d、点M1，单击“构造”菜单中的“轨迹”，出现轨迹对话框，范围（在厘米）选-100≤d≤100，单击“确定”。选中参数d、点M2，单击“构造”菜单中的“轨迹”，出现轨迹对话框，范围（在厘米）选-100≤d≤100，单击“确定”。隐藏点M1、M2，直线L′，圆，直角坐标系。改变参数e的大小，当0<；e<；1时，轨迹是椭圆（图1）；当e=1时，轨迹是抛物线（图2）；当e>；1时，轨迹是双曲线（图3）。

编辑 温雪莲