断层力学参数反演及其对地应力场扰动效应研究

李永松 ，陈建平，尹健民 ，许 静

（1.中国地质大学 （武汉）工程学院，湖北 武汉 430074；2.长江科学院水利部岩土力学与工程重点实验室，湖北 武汉 430010）

0 引 言

岩体中的断层及不连续面的存在影响着岩体中的应力变化及其迁移过程，在应力应变协调的过程中使断层及不连续面附近的局部应力和区域应力之间有相当大的差别。从某种意义上来讲，断层是区域地壳稳定和工程岩体失稳的主控因素之一。在实际工程中，为研究断层对应力场的扰动效应，很多学者从断层周围地应力测试[1-4]及数值模拟等方面进行了相关研究。从目前的研究发展趋势来看，主要有以下3种途径:①把断层抽象为被节理及裂隙分割的块体系统进行力学分析[5-6]；②把断层的力学性态作为附加条件，采用连续介质力学的方法进行模拟[7-8]；③采用接触面单元模拟断层与岩体之间的不连续面[9]。

在实际工程中，断层的几何形体是易于确定的，而其力学性态往往难以确定，且力学性态是影响断层及其周边应力场分布的主要因素，特定的断层力学参数与特定的应力分布状态相匹配。本文利用断层附近及其周边测孔的测试资料，结合正交设计理论及人工神经网络的非线性反演方法对断层的力学参数进行反演，并对断层对应力场的扰动效应进行研究。

1 测孔布置及测试结果

1.1 地质概况及测孔布置

某隧道位于福建东部重力梯度带上，隧道走向为N70°W，山脉主要走向为北北东～南南西，场区以构造剥蚀中低山为主，岩性以灰色、浅灰色钙质粉砂岩为主。为研究隧道轴线部位岩体应力分布情况及断层对应力场的扰动效应，布置了1、2号2个测孔进行常规的水压致裂法地应力测试 （见图1），其中2号测孔位于断层F11和F12中间。F11断层的产状为135°∠75°，断层带内发育2条断面，使岩层产生一定错动，带内岩石破碎，断面呈舒缓波状，为压性逆断层。断层上盘影响宽度约25 m，下盘约10 m，节理裂隙发育，较破碎。F12断层产状为157°∠59°，断层带内为硅化、叶腊石化碎裂岩，见断层泥及磨圆的断层角砾，断面略呈舒缓波状，断面上发育阶步及擦痕，为压性逆断层。断层上、下盘影响宽度约20 m，节理裂隙发育，较破碎。

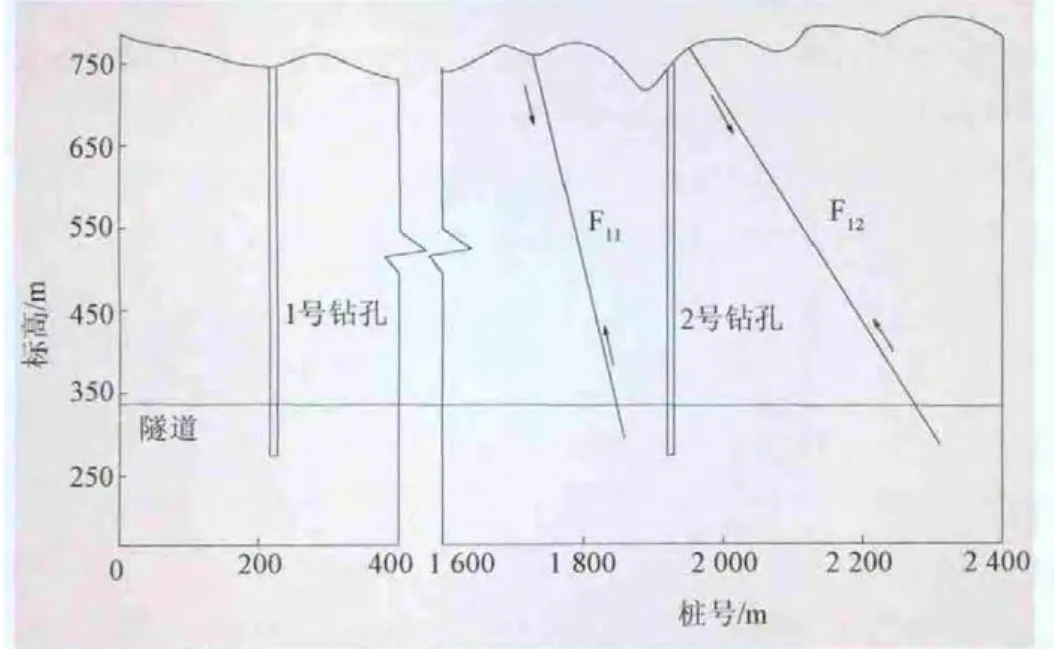
图1 钻孔布置

1.2 地应力测试成果分析

由图1可知，1号测孔距离断层较远，其应力分布不受断层的影响，且测试区域内地势起伏相对较小，其应力分布情况可视为测试区域内的应力分布；2号测孔断层位于断层F11和F12之间，其应力分布受复合断层的影响较大。由测试成果可知，1号测孔测试区域内最大水平主应力方位位于N25°～30°W之间，而2号测孔位于N7°～23°E之间，两者夹角较大。若将1号测孔测得的最大水平主应力方位视为区域构造应力方位，则2号测孔所在部位的最大水平主应力方位受断层的影响偏离区域构造方位高达约45°。

图2给出了2个测孔测得的最大和最小水平主应力随深度的变化情况 （图中，σH为最大水平主应力，σh为最小水平主应力，σz为自重应力）。由图2可知，1号测孔应力量值整体大于2号测孔。线性拟合可知，1号测孔最大水平主应力侧压系数λ（λ=σH/σz） 约为 1.6，而 2号测孔约为 1.3。 2 号测孔最大水平主应力方位的偏转及应力量值的弱化可归结为断层的扰动效应。

图2 测试成果

2 断层力学参数反演

2.1 计算模型及边界条件

为方便建模，并消除边界效应的影响，建模时X轴取为隧道走向方位N70°W，使断层及2号测孔处于计算模型的中部，计算范围取1200 m×1200 m。根据1号孔测试结果，取最大水平主应力方位为N30°W、侧压系数为1.56，最小水平主应力侧压系数为1.04。由于最大水平主应力方位与计算坐标系中的X轴呈40°夹角，需将计算模型上的最大及最小水平主应力转化为边界上的应力分量σx、σy和τxy，计算公式如下

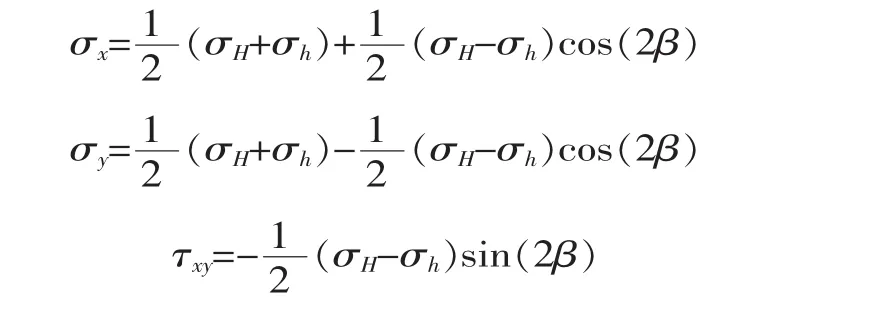
式中，β为最大水平主应力方位与计算坐标X轴的夹角。

2.2 断层参数反演

本文采用连续介质力学的方法，将断层及其影响带内的岩体参数进行弱化。在一定的构造应力及自重应力组成的应力场中，由于断层的扰动效应，断层及其周边的应力将出现应力分异现象，但应力分布情况与断层的力学参数相适应，且这种应力-断层参数的响应十分复杂，不能用简单的线性方程表示。因此，采用基于正交设计的人工神经网络非线性反演模型对断层参数进行反演。

分别取断层F11、F12的弹性模量E11、E12为0.5～4.5 GPa，F11、F12的泊松比 μ11、μ12分别为 0.25～0.41。选择U9*（94）表进行设计，每个因素取9个水平，各水平组合见表1。

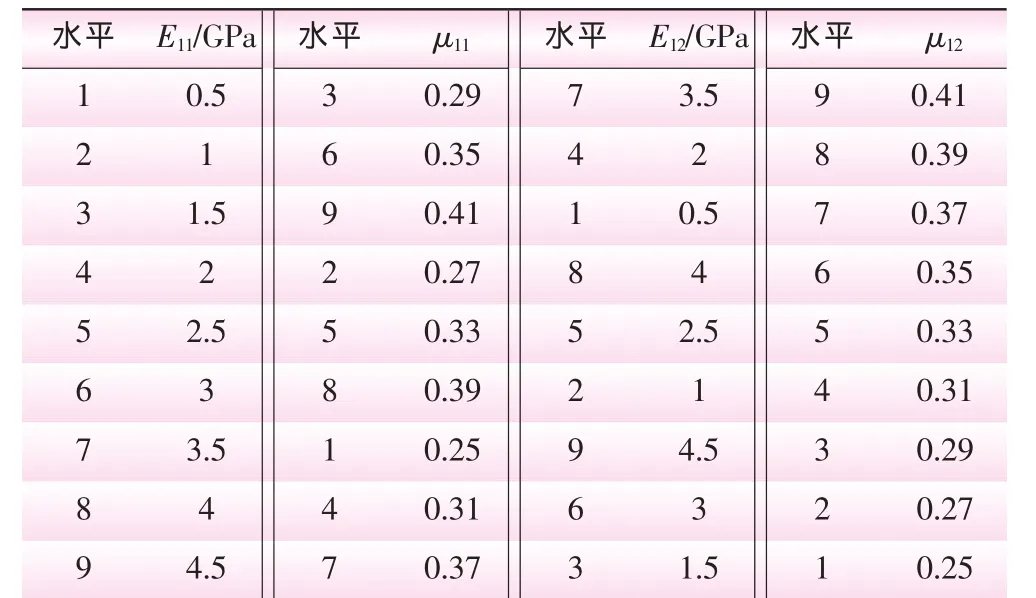
表1 各因素水平组合

进行有限元正向计算，将每种工况下的2号测孔测点对应的应力量值的计算结果作为神经网络的输入，对应的断层力学参数作为输出进行神经网络训练。神经网络训练时采用Levenberg-Marquardt算法，以保证误差函数总是减小的。训练完成后，得到了测点的应力值与断层力学参数之间的非线性映射关系。此时，以2号测孔测点的实测值作为输入，可得断层力学参数。其中，E11=3.12 GPa，μ11=0.351，E12=2.85 GPa，μ12=0.370。 表 2给出了部分测点的计算值和实测值的对比。计算值与测试值的复相关系数为0.886，说明反演结果比较可信。

表2 计算值和测试值的比较

3 断层对应力场的扰动效应分析

根据模拟结果，图3、4分别给出了隧道底板高程X与Y方向正应力分布剖面图和沿隧道轴线方向平面应力分量变化曲线 （图中，Sxx为x向正应力，Syy为y向正应力，Sxy为xy向剪应力）。由图3和图4可知，断层附近应力量值的变化较为复杂，断层端部 （尖灭处）有明显的应力集中，且长度较大的断层F12端部的应力集中程度和集中的范围明显大于规模相对较小的F11断层；应力降低的情况表现为在断层附近应力值较低，且在断层厚度较大的F11断层内部应力松弛的程度相对较大；随着距离的增加，主应力逐渐增大，到一定距离后，趋于稳定。

图3 正应力分布

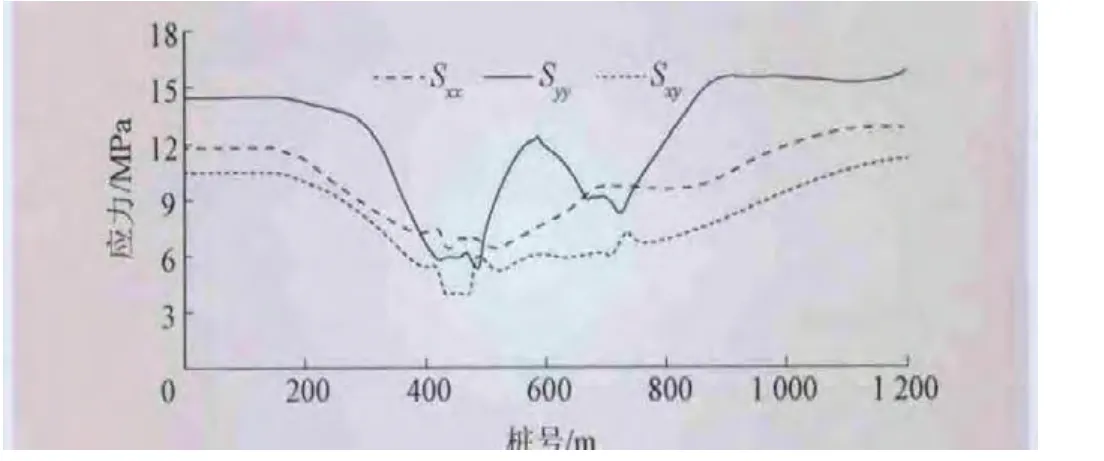
图4 隧道轴线平面应力分量分布

由于断层的扰动效应，断层附近最大水平主应力方位也明显变化，而这种变化主要限于断层附近一定距离内。在断层内及其附近最大水平主应力方位与断层走向平行或呈小角度相交，而断层尖灭处最大水平主应力方位与断层走向呈大角度相交，随着距离的增加最大水平主应力方位趋于与构造应力方向平行。

4 结 语

断层对地应力场的扰动十分复杂，且断层的力学参数亦难以确定，本文基于现场地应力实测资料，通过对断层的力学参数进行反演及断层对应力场的扰动效应进行分析，可以得出以下结论:

（1）测孔测点的测试值和模拟计算结果一致，说明本文将断层及其影响带简化为连续介质，并通过力学参数的正交设计采用神经网络的非线性反演方法是合理可行的。

（2）由于断层的扰动效应，断层内部及附近区域有明显的应力分异现象，应力量值降低，且断层厚度越大，应力松弛程度越大；在断层端部 （尖灭处）出现明显的应力集中现象，断层长度越大，应力集中的程度越高。

（3）在断层内及其附近区域最大水平主应力方位受断层走向控制，与断层走向基本平行，而在断层尖灭处最大水平主应力方位与断层走向呈大角度相交。

［1］苏生瑞，STEPHAN S O，王士天.瑞典爱斯泼硬岩实验场地应力研究［J］.工程地质学报，2001，9（1）:100-106.

［2］沈海超，程远方，赵益中，等.基于实测数据及数值模拟断层对地应力的影响［J］.岩石力学与工程学报，2008，27（S2）:3985-3990.

［3］黄醒春，夏小和，沈为平.断层周边应力场的原位实测及数值反演［J］.上海交通大学学报，1998，32（12）:55-59.

［4］TAN Z Y，CAI M F.Measurement and study of distributing law of in-situ stresses in rock mass at great depth［J］.Journal of University of Science and Technology Beijing,2006,13（3）:207-212.

［5］RAWNSLEY K K.Joint development in perturbed stress field near fault［J］.J.Struct.Geol,1992,14（8-9）:939-951.

［6］王红才，王 薇，王连捷，等.油田三维构造应力场数值模拟与油气运移［J］.地球学报，2002，23（2）:175-178.

［7］马淑芝，贾洪彪，易顺民.罗湖断裂带地应力场三维有限元模拟分析［J］.岩石力学与工程学报，2006，25（增 2）:3898-3903.

［8］黄醒春，卢海星.复杂断层扰动下的原岩应力场的数值分析与评价［J］.岩土工程学报，2000，22（3）:327-331.

［9］GOODMAN R E.Methods of geological engineering in discontinuous rocks［M］.USA:West Publishing Co.,1976.