赏析2014年高考新课标全国卷Ⅰ第25题

司德平

（河南省郑州外国语学校，河南 郑州 450001）

2014年高考课标Ⅰ卷第25题是一道物理压轴题，考查了平抛运动的规律、匀强电场等势线与电场线的特点及关系、带电体在复合场中运动的功能关系.现不同于参考答案，利用平抛运动的矢量直角三角形法和匀强电场的电势等分法及对称性，解答本题.

图1

原题.（2014年高考课标Ⅰ卷第25题）如图1所示，O、A、B为同一竖直平面内的3个点，OB沿竖直方向，∠BOA＝60°，OB＝OA.将一质量为m的小球以一定的初动能自O点水平向右抛出，小球在运动过程中恰好通过A点.使此小球带电，电荷量为q（q＞0），同时加一匀强电场，场强方向与OAB所在平面平行.现从O点以同样的初动能沿某一方向抛出此带电小球，该小球通过了A点，到达A点时的动能是初动能的3倍；若该小球从O点以同样的初动能沿另一方向抛出，恰好通过B点，且到达B点时的动能是初动能的6倍，重力加速度大小为g，求：

（1）无电场时，小球到达A点时的动能与初动能的比值；

（2）电场强度的大小与方向.

1 利用平抛运动的矢量直角三角形法解答第（1）问

通常，处理平抛运动的基本思想是化曲线运动为直线运动，即根据合运动与分运动的独立性、同时性和等效性，把平抛运动正交分解为水平初速度方向的匀速直线运动和竖直方向的自由落体运动.速度和位移的合成与分解，可由矢量运算的平行四边形定则简化为三角形定则，因此，可利用矢量直角三角形法解决平抛运动问题.

在平抛运动中，过抛物线上的任一点做切线，速度方向的反向延长线必然通过对应水平位移的中点，且该点速度的偏向角α与对应平抛位移的水平方向角β，满足tanα＝2tanβ.平抛物体的速度直角三角形与相应位移直角三角形分别将水平速度、竖直速度、初动能、末动能、水平位移、竖直位移和抛出点的重力势能有机地整合在这两个三角形当中，即平抛三角形集合了平抛物体的位移关系、速度关系和能量关系.

解析：在无电场时，小球运动为平抛运动.设小球的初速度为v0，初动能为Ek0，小球在A点的动能为EkA，A点相对抛出点O的高度为h，A点速度的偏向角为α，由平抛运动的速度直角三角形与位移直角三角形的关系可知

由（1）、（2）式可得

由动能定理可知

由（3）、（4）式可得

或由（1）、（2）式可得抛出点的重力势能与初动能之比为

由（4）、（5）式也可得

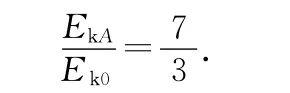
2 利用匀强电场的电势等分法及对称性解答第（2）问

匀强电场的等势线不仅与电场线垂直，而且是疏密均匀的平行线.因此，在匀强电场中，虽然沿任意一个方向电势的降落都是均匀的，但是沿不同的方向电势降落的梯度一般是不同的.当相交的两直线关于场强方向对称时，在相交的两直线上等距离的两点电势必相等.该两点的连线为等势线，与场强方向垂直，且沿场强方向电势降落最快.因此，匀强电场可利用电势等分法及对称性寻找等势点，进而根据等势线与电场线关系，确定场强的方向；再由E＝求场强的大小.

解析：在无电场时，由（3）式可知

又因为

由（6）～（8）式可得

加上与△OAB所在平面平行的某一方向匀强电场E后，对带电小球从O到A和从O到B的过程，分别由动能定理可知

又因为

由（9）～（12）式可得

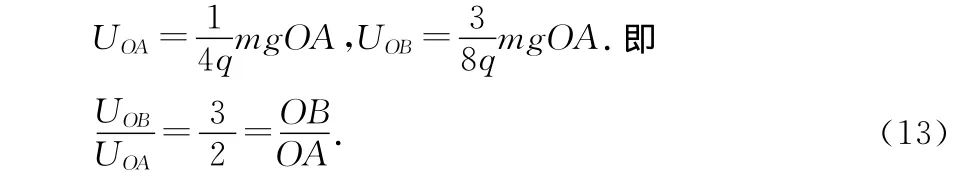
图2

由（13）式可知OA和OB关于场强方向对称，在OB上取一点C，令OC＝OA＝OB，则A、C为等势点，A、C连线为等势线，过O点做A、C连线的垂线.由几何关系可知，场强方向沿∠BOA的角平分线.如图2所示.

设场强方向与OB间的夹角为？θ，则有θ＝30°.根据正电荷从O到B

电场力做正功，可判断电场方向与竖直方向成30°夹角斜向右下方.匀强电场场强的大小为

平抛运动的矢量直角三角形法可以迁移、处理类平抛运动问题.无独有偶，2014年高考山东卷理综第18题就可以利用类平抛运动的速度直角三角形法、结合对称性简便处理.

图3

原题.（2014年高考山东卷理综第18题）如图3所示，场强大小为E、方向竖直向下的匀强电场中有一矩形区域abcd，水平边ab长为s，竖直边ad长为h.质量均为m、带电荷量分别为＋q和-q的两粒子，由a、c两点先后沿ab和cd方向以速率v0进入矩形区（两粒子不同时出现在电场中），不计重力.若两粒子轨迹恰好相切，则v0等于