巧用整体法 妙解连接体

陈燕琴

（浙江省回浦中学，浙江 台州 317000）

在高中力学题中有一类常见题型便是连接体问题，整体法与隔离法是解决该类题型的常用方法.我们将系统内物体间的相互作用力称为内力，系统与外界的相互作用力称为外力.整体法的优点在于只需分析整个系统与外界的关系，避开了系统内部繁杂的相互作用，从而更简洁、更本质地展现出物理量间的关系.缺点是无法讨论系统内部相互作用的情况.当求系统内物体间的相互作用力时，则需将某个物体从系统中隔离出来进行受力分析.因此整体法往往与隔离法结合使用，二者处于既合作又分工的关系.解决具体问题时，合理使用整体法，可充分发挥它的优点，使解题过程简捷、迅速、明了，从而达到有效的提高学生解题效率的目的.

图1

例1.如图1所示，物体A靠在竖直墙面上，在力F作用下，A、B保持静止，求墙面对物体A的弹力大小.

解析：若以物体A为研究对象，由于物体B对物体A及墙面对物体A的作用力的不确定，使得对物体A的受力分析变得复杂.倘若以物体A和物体B整体为研究对象，就可以避开这个问题，对整体而言，物体受重力及竖直向上的力F，再结合整体的平衡状态可知，墙面对物体A的弹力为0.

连接体问题常可分为3类：其一，系统处于平衡状态，即物体处于静止状态或者匀速直线运动状态.其二，系统以相同的加速度做变速运动，如匀变速直线运动，匀速圆周运动等.其三，系统内各物体以不同的加速度运动.针对上述3类问题，均应采用与之相对应的方法来求解.

1 系统处于平衡状态

若求外力，首选整体法，对系统进行受力分析，再根据系统平衡条件分别对不同对象进行分析，或以部分为研究对象，或以某个物体为研究对象，逐步求解.若求系统内物体间的相互作用力，则选择受力个数相对少的物体或部分从系统中隔离出来对其受力分析，再辅以整体法交替灵活使用.

图2

例2.如图2所示，在两块相同的竖直木板间，有质量均为m的4块相同的砖，用2个大小均为F的水平力压木板，使砖静止不动，则左边木板对第1块砖，第2块砖对第3块砖的摩擦力分别为

（A）4 mg，2 mg. （B）2 mg，0.

（C）2 mg，mg. （D）4 mg，mg.

解析：各砖块间相互作用力的不确定使得对砖块的受力分析变得繁杂.若将4个砖块看作一个整体，受力分析如图3所示.由平衡条件可知f1＝f4＝2 mg.再以砖块1和砖块2整体为研究对象受力分析如图4所示，由平衡条件可知，第2块砖与第3块砖间的摩擦力为0，答案选（B）.

图3

图4

2 系统以相同的加速度做变速运动

解此类题型常用方法：若所求的是外力，则先用隔离法对系统内物体进行受力分析，利用牛顿第二定律求出该物体的加速度，再利用整体法及牛顿第二定律求出外力.若所求的是内力，则先用整体法对系统受力分析，再利用牛顿第二定律求出系统的加速度，最后用隔离法及牛顿第二定律求出内力.总之，以物体的加速度作为内力和外力的联系纽带.

例3.航天员在航天器中绕地球做匀速圆周运动时，航天员处于完全失重状态，试证明之.

解析：很多学生不理解为什么航天器中航天员会处在完全失重状态，不是有重力吗？又例如将底端带有小孔的瓶子装满水自高处自由落下，在不计空气阻力时，为什么水不会漏出来？理解此类问题，就需有一个整体的意识.

以航天器整体为研究对象，设航天器及内部物体总质量为M，航天员的质量为m，航天器运行的轨道半径为R，且航天员在航天器中所受的支持力为FN，则有

再以航天员为研究对象有

易解得FN＝0，即航天员处在完全失重状态.同理，可以理解为什么处于自由落体状态的瓶子里的水不会漏出来.

图5

例4.如图5所示，在倾角为30°的光滑斜面上放置质量分别为m和2 m的4个木块，其中两个质量为m的木块间用一不可伸长的轻绳相连，木块间的最大静摩擦力是fm，现用平行于斜面的拉力F拉其中一个质量为2 m的木块，使4个木块沿斜面以同一加速度向下运动，则拉力F的最大值是

解析：此题的难点在于系统内物体较多，且物体间的摩擦力大小、方向不明确.此时若能巧妙利用整体法可使问题简化.研究木块1、2间的摩擦力时，先以4个木块整体为研究对象，经受力分析可知系统的加速度满足a＝gsin30°＋F／（6 m）.再以木块1、3、4整体为研究对象可知木块1所受的摩擦力沿斜面向下，且有f21＝4 ma-4 mgsin30°.研究物块3、4间的摩擦力，可以木块4作为研究对象，由a可知，木块4所受的摩擦力方向沿斜面向下，且有f34＝2 ma-2 mgsin30°.由此可知，当木块1、2间的摩擦力达到最大静摩擦力时，拉力F达最大值.综上可知，答案选（C）.

3 系统内各物体以不同的加速度运动

解此类题型常用质点系牛顿第二定律，虽然该部分内容在高中期间不要求，但若能让学生了解该部分内容，很多棘手的问题都可以迎刃而解.质点系牛顿第二定律可叙述为：质点系的合外力等于系统内各质点的质量与加速度乘积的矢量和.即

这里假定质点系中有n个质点具有对地的相对加速度.运用时可将系统所受的外力及各物体的加速度按选定的直角坐标系进行正交分解，即

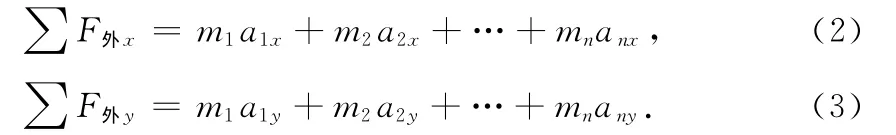
此时，受力分析过程中，可不考虑系统内物体间的相互作用力，从而达到简化解题过程的目的.当然，质点系牛顿第二定律同时也适应于上述所提到的第一类和第二类问题，甚至在有些问题中比上述2种方法还要简便.

图6

例5.如图6所示，粗糙的水平地面上有一斜劈，斜劈上一物块正在沿斜面以速度v0匀速下滑，斜劈保持静止，则地面对斜劈的摩擦力

（A）等于0.

（B）不为0，方向向右.

（C）不为0，方向向左.

（D）不为0，v0较大时方向向左，v0较小时方向向右.

解析：由于2个物体都处在平衡状态，故根据质点系牛顿第二定律可知两物体组成的系统在水平方向的合外力为0，即答案选（A）.

图7

例6.如图7所示，在水平面上的箱子内，带异种电荷的小球A、B用绝缘细线分别系于上、下两边，处于静止状态.箱底受地面支持力为N，球B所受细线的拉力为F.剪断连接球B的细线后，在球B上升过程中箱底受地面的支持力

（A）小于N. （B）等于N.

（C）等于N＋F. （D）大于N＋F.

解析：以3个物体组成的系统为研究对象，设箱子、小球A和B的质量分别为m、mA、mB，球B的加速度为a.由质点系牛顿第二定律可知箱子受到地面的支持力满足

对小球B有 FAB-mBg＝mBa，

绳刚剪断时 FAB-mBg＝F.

又因为小球B上升的过程中，两球间的相互作用力FAB逐渐变大，故小球B上升过程中有mBa＞F.即答案选（D）.

质点系牛顿第二定律在解决连接题问题，特别是系统内质点以不同的加速度运动时可以带来极大的便利.但是学生在初学时往往对其持有“怀疑”心态.因此，在具体的教学过程中建议先用常规的方法解题，再利用质点系牛顿第二定律循序渐进，一方面让学生充分感受到该方法的便捷，另一方面有助于学生的理解、接受及学生知识的内化.

在运用整体法解决涉及竖直方向上外力的问题时，还可引用超重（或失重）的方法解题.例如上述例6中剪断绳子后，球B向上以加速度a加速，处超重状态，超重mBa.因此箱底受到地面的支持力大小为N＋mBa.因为球B上升过程中a逐渐变大，且绳子剪断瞬间F＝mBa，故（D）正确.该方法本质上与质点系牛顿第二定律相同，但因为学生有理论基础，因此较之更容易接受和理解.

综上所述，在分析两个或两个以上物体组成的系统与系统外物体间的相互作用力时，应首选整体法.而在分析系统内物体间的相互作用力时，需考虑用隔离法.何时用整体法何时用隔离法，只有在分析到位后，才能真正实现“巧用”二字.

整体法和隔离法不仅适用于力学问题，而且在电磁学中也有不少应用.如果我们在平时教学中能将两种方法融会贯通，灵活应用，一定能达到加快解题速度，提高解题效率，实现事半功倍的目的.

1 王朝银.创新设计 高考复习（物理）［M］.杭州：浙江教育出版社，2012.6.

2 所广一，王玉栋.5年高考三年模拟：B版 高考物理［M］.北京：首都师范大学出版社，2011.5.

3 陈益富.连接体问题归类分析［J］.物理教师，2014（2）：89-91.