用角速度比较法求复摆的周期

陆天明

（南京师范大学附属中学江宁分校，江苏 南京 211102）

在重力场中，将一任意形状的不可形变的物体（刚体）穿过水平轴悬挂起来，使其做小角度摆动，不计一切阻力和摩擦力，这就构成了复摆，复摆又称物理摆，如图1所示，其中rC为悬挂点O到质心C的距离.对某一确定的复摆，其微小振动的周期是一个定值.复摆周期公式的证明较为复杂，通常要用到高等数学的知识.其实可以通过对复摆转动的角速度进行分析并与单摆进行比较，可以巧妙地得到复摆的周期公式.

这里需要特别说明的是，虽然全国中学生物理竞赛对质点和质点组的角动量定理、角动量守恒定律提出了要求，并明显地反映在多年来的竞赛试题中，但同时也明确提出不引入转动惯量的概念，这是令竞赛教练们感到费解的地方.实际上，在分析相关赛题时，都要运用转动惯量的概念.所以笔者认为，在实际的教学中根本没有必要回避转动惯量这个重要的物理概念，而且笔者在实际教学中发现，学生对转动惯量的理解并没有多少困难.

学生一旦有转动惯量的概念，就可以讨论上述复摆的周期问题了.对于这个问题，学生们最容易犯的错误就是想当然地认为复摆的周期为

图1

怎样用初等方法求出复摆的周期呢？

如图1所示，设复摆的幅角为θ0，那么当复摆摆到任一个角度θ时，由机械能守恒得

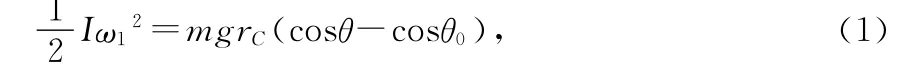
式中I为复摆绕悬挂点O的转动惯量.在任一个位置的角速度为

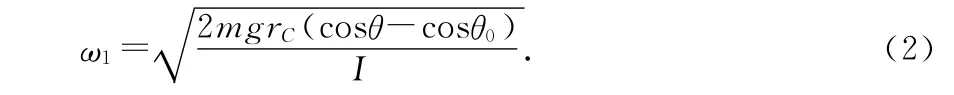
如图2所示，构造一个单摆，设其摆长为l，幅角也为θ0，则当单摆摆到任一角度θ时，由机械能守恒得

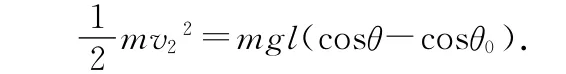
在任一位置的速度为

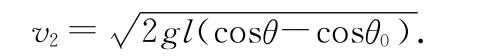
由线速度和角速度的关系v2＝ω2l，可以得到

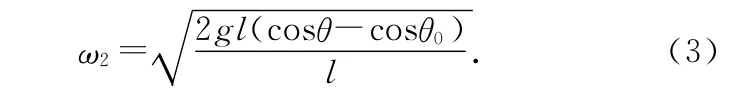
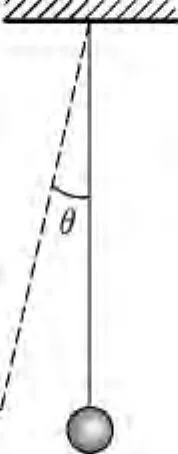
图2

由（2）、（3）两式可知

对于一个复摆和单摆，因为m、I均不变，即在任一角度θ处，角速度之比都是一个定值，所以两种摆的周期之比也应为

当然也可以通过简单的数学推导.对于任意一个无穷小的角位移Δθ，复摆和单摆所用时间分别为Δt1＝和Δt2＝，所以有

周期为无数个这些小时间段之和，即复摆的周期为T1＝ ∑Δt1，单摆的周期为T2＝ ∑Δt2，所以有

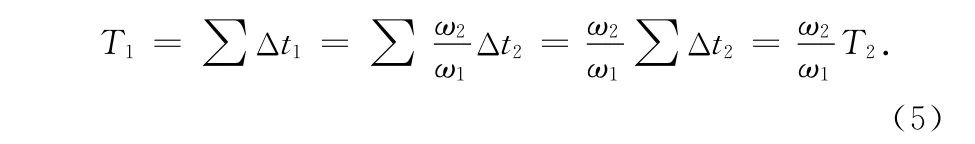
代入（4）式可得

最后还要说明的是，一般情况下复摆的转动惯量不等于I＝mrC2，所以一般l0≠rC，所以我们不能想当然地认为复摆的周期相当于一个摆长为rC的单摆的周期，即认为复摆的周期为的想法是错误的.

1 李增林.力学［M］.南京：南京工学院出版社，1988：269-270.