精密线振动特性离心机的误差分析

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001)

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001)

精密线振动是实现高阶误差项测试的有效方法，误差分析则是保证其测试方案完善、测试精度提高的关键。在高精度加速度计测试中，微小的设备误差对测试结果的影响往往无法忽略，为进一步提高测试精度，需要对测试设备的误差进行分析。我们首先给出了具有精密线振动特性离心机的工作原理和输出特性；然后建立包含安装误差和设备误差的离心机模型，并根据动态加速度合成定理，采用矢量方法推导出离心机输出加速度表达式；最后分析了在加速度计坐标系下，双轴离心机产生正弦加速度时，每个非独立误差源对加速度计输入比力的影响，为解决精密线振动试验方案设计和误差补偿研究提供了理论参考。

精密离心机；旋转平台；误差分析；线振动；过载加速度

随着航天、航空技术的不断发展，飞机、火箭、导弹的导航精度不断提高[1]，对惯性仪表测量精度也不断提出新的要求，高精度惯性元器件的高阶非线性误差越来越不容忽视，对惯性仪表高阶非线性误差测试设备测试方法的研究也在逐步深入。精密线振动特性的离心机就主要用于高精度陀螺仪、加速度计、捷联惯导系统和惯导平台等的高阶非线性误差校准与测试。通常加速度计的一阶线性标度因数主要由 1g重力场下的翻滚试验确定，但翻滚试验的输入加速度较小，不足以激发加速度计的高阶非线性误差。而在实际应用中，加速度计通常需要工作在大过载环境中，例如，发射段的加速度可达6～30 g，再入段加速度则高达近百 g，这些阶段中存在着严重的高阶非线性误差，其测试结果将影响导航系统的实际精度。目前用于加速度计过载实验的设备主要有离心机、振动台、火箭橇、空气炮、压杆等。火箭橇、空气炮、压杆提供的是瞬时加速度，而加速度计误差系数校准需要连续的过载加速度输入；实验室易获得的振动台多为电磁振动台，其精度等级较低且在低频段失真严重，即使是专门设计的高精度线性振动台也面临着加速度的幅值和频率的耦合问题；精密离心机能够输出连续恒定的加速度，可作为加速度计的静态测试设备[2]，对非陀螺型加速度计有很好的测试效果，但对于陀螺仪和陀螺积分加速度计的测试因旋转而引入额外的误差。在离心机的基础上研制的带旋转平台的离心机可实现精密线振动特性，不但可以与离心机同步反转、隔离离心机旋转角速度给陀螺仪和陀螺加速度计带来的额外误差，还可以根据测试需要分别控制旋转平台与离心机转速，作为加速度计的动态测试设备使用，满足更广泛的测试需求，尤其是能够用于频率与幅值不耦合情况下输出动态加速度的精密线振动试验。

目前国内针对双轴离心机的研究还比较少，仅有少量相关文献，尚无对带旋转平台离心机的输出加速度及其误差进行详细分析的文献。文献[3]介绍了非陀螺线性加速度计在单旋转轴离心机下的详细测试设计与流程，并将测试中的误差源和其产生的影响进行了详细介绍。文献[4]分析了带同步反转平台的离心机误差对陀螺测试的影响，并研究了离心机误差对陀螺漂移系数的影响，但由于陀螺标定需要的输入量为旋转角速度，所以未涉及到加速度分析。文献[5]讨论了存在质量偏心时离心机的输出情况，没有进行设备误差分析，并且文献[5]中设定检测质心偏差 r、加速度计输入轴和旋转平台臂轴是沿同一方向，未考虑未对准误差，实际上检测质心的偏差和加速度计制造及加速度计安装都有关系，同时r的方向和大小都难以检测，不能完全与加速度计输入轴方向重合。

本文针对实际工程情况，首先说明了带旋转平台的离心机工作原理，建立了带安装误差的离心机模型；然后基于向量求导法在考虑安装误差的情况下分析离心机加速度合成，研究其输出加速度及误差情况，并计算出离心机输出加速度和基于线振动特性离心机测试的加速计输入比力，分析了加速度计的质量偏心方向和大小都未知的情况对加速度计输入量的影响，同时研究了轴系未对准误差、安装误差、回转误差、速率不确定性和半径不确定性给加速度计标定带来的影响；最后对比加速度计实际输入加速度和理论加速度输入值，分析了各项非独立误差源对加速度计输入比力的影响。

1 带旋转平台离心机的工作原理

目前常见的线振动输出设备为线性振动台，它的输出加速度在行程一定的情况下与频率成正比，低频的情况下无法输出大的加速度，在行程有限的情况下无法对指定幅值的加速度进行多频率输出。而带旋转平台离心机由于有两个旋转自由度，可以使离心机产生过载（线振动幅值），实现旋转平台正弦振动，避免了线性振动台所产生的问题，并且具有更灵活的使用功能，满足更广泛应用需求。

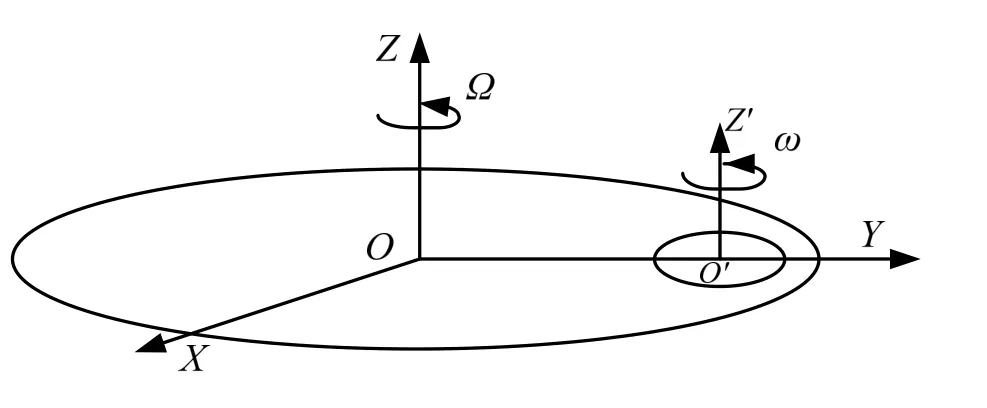
图1 带旋转平台离心机工作原理图Fig.1 Schmatic of centrifuge with rotation platform

2 带旋转平台离心机输出加速度的合成

为了满足实际测试需要，以下将考虑离心机、旋转平台安装误差和离心机设备误差，建立包含这些误差信息的离心机模型，离心机向量模型如图2所示。

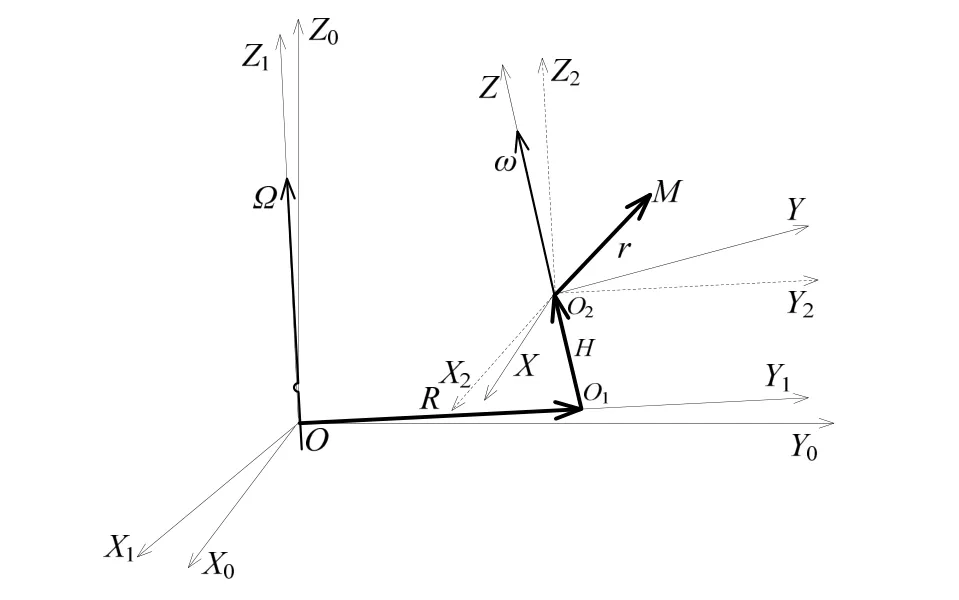
图2 离心机向量模型Fig.2 Vector model of centrifuge

坐标系 OX0Y0Z0为地理坐标系，OZ0轴沿当地重力方向。坐标系OX1Y1Z1为离心机坐标系，可由地理坐标系OX0Y0Z0依次绕OX0轴旋转ξ角，再绕OY0轴旋转η角获得，其中ξ角为O0Z1轴在Y0O0Z0平面的投影与O0Z0轴的夹角，η角为O0Z1轴在X0O0Z0平面的投影与O0Z0轴的夹角；沿OZ1轴为离心机主轴，其角速度矢量为Ω；OY1轴上的点O2为O2Z轴与OY1轴的交点，是旋转平台与离心机的固连点。坐标系O2XYZ为旋转平台坐标系；O2Y轴为旋转平台轴心到夹具安装点的连线，是加速度计输入轴的理论方向；O2Z轴旋转平台回转轴，其角速度矢量为 ω。辅助坐标系O2X2Y2Z2与坐标系OX1Y1Z1平行，坐标系O2XYZ可由坐标系O2X2Y2Z2依次绕O2X2轴旋转α角，绕O2Y2轴旋转β角，使Z2轴与Z轴重合后再绕O2Z轴旋转γ角获得；当旋转平台转动时，γ = γ0+ ωt ，γ0为初始未对准角，α角为O0Z轴在Y2O2Z2平面的投影与O2Z2轴的夹角，β角为O2Z轴在X2O2Z2平面的投影与O2Z2轴的夹角。加速度计检测质心位于M点，O2M与O2Y轴的夹角为θ。

上文提到的ξ、η、α、β角为离心机的安装误差，也称为轴系未对准误差，精密线振动特性的离心机要求轴系未对准角误差为角秒级。

2.1 安装误差的影响

对式(1)两边同时求导，得检测质量块敏感中心M点的速度为：

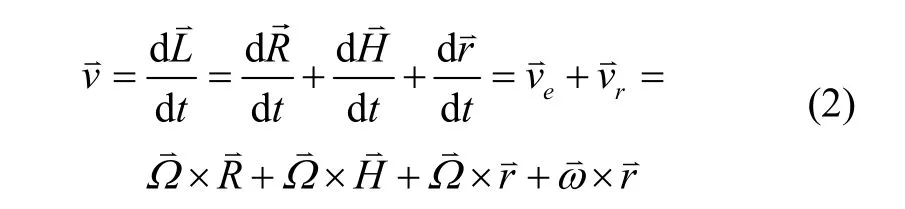
对式(2)再次求导，得检测质心M点的加速度为

而

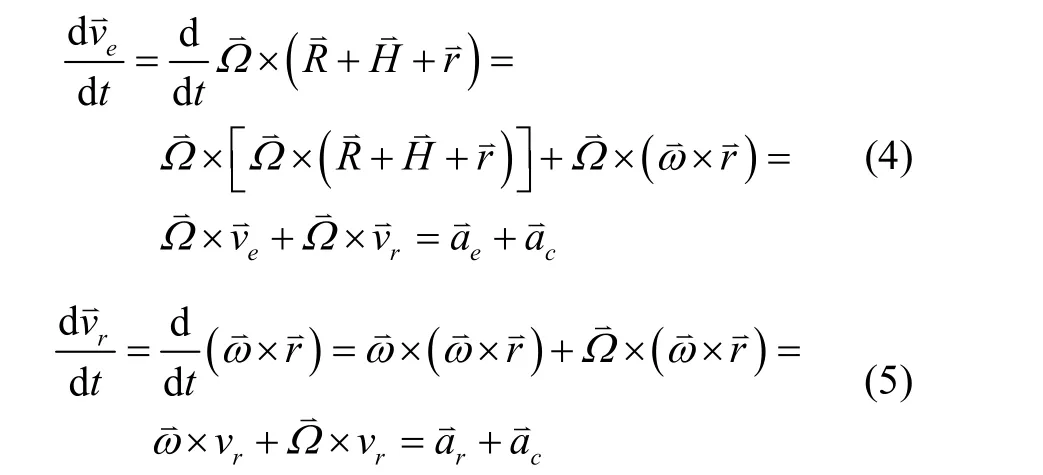
所以

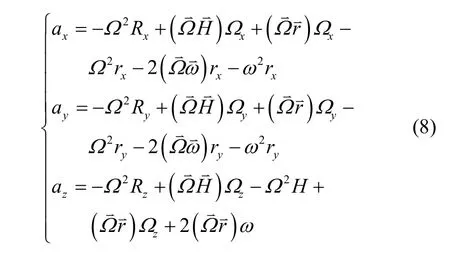
根据坐标旋转关系可以得到：

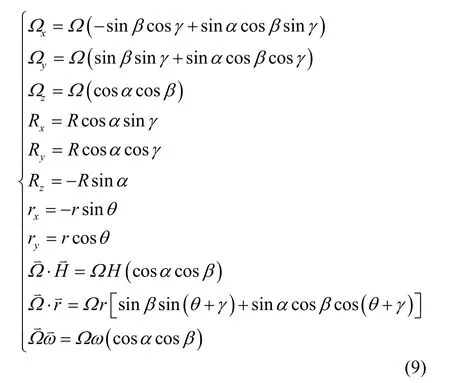
当旋转平台转动时有 γ = γ0+ ωt 。如果将式(9)直接代入式(8)，得到的结果过于复杂，需要先进行简化。

精密线振动特性的离心机要求轴系未对准角误差ξ、η、α、β为角秒级误差角，可以使用小角度简化。当ε→0时，有cosε ≈1，sinε ≈ ε。进行小角度化简时需验证简化误差是否合乎设备误差要求，验证如下：

设ε =1×10-4rad，则sinε=1.000 000 015×10-4，cosε=0.999 999 995，因此当 ε≤1×10-4时，ε与 sinε之间的误差小于0.2×10-11，cosε与1之间的误差小于0.5×10-8，都远小于规定的设备精度（10-6数量级），因此当安装误差角小于1×10-4rad时可适用于小角度化简。

精密线振动特性振动台规定安装误差为角秒级，符合ε≤1×10-4rad ≈ 20.6″的假设，设备误差满足化简条件，且简化误差满足设备精度要求。

将cos α=1、sin α=α、cos β=1、sin β=β代入式(9)中，并将式(9)代入(8)中，得简化后的离心机输出沿旋转平台坐标系方向的加速度分量为：

式中，α、β、r、H是安装误差，这四项中任意两项或以上的连乘积为高阶小项，忽略高阶小项，则：

2.2 设备误差的影响

考虑离心机的半径测量误差和角速率误差，有：

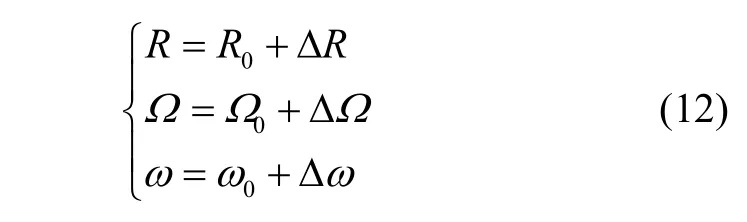
将式(12)代入式(11)中，并忽略高阶小项，得离心机输出加速度表达式为：

同样得到沿旋转平台坐标轴的重力加速度分量为：

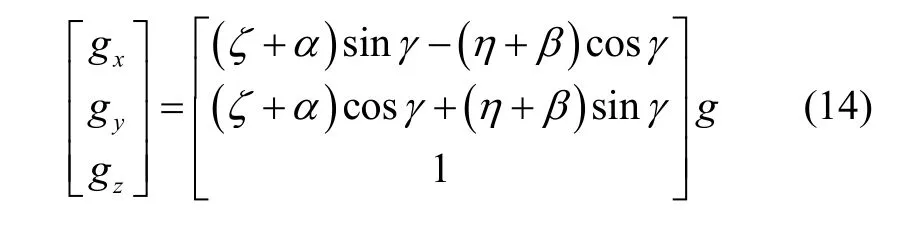
式(11)和式(14)中， γ= γ0+ ωt 。

2.3 离心机主轴回转误差的影响

考虑离心机主轴回转误差，由文献[6]可得回转误差引起的在旋转平台坐标系O2XYZ下的输入加速度误差为：

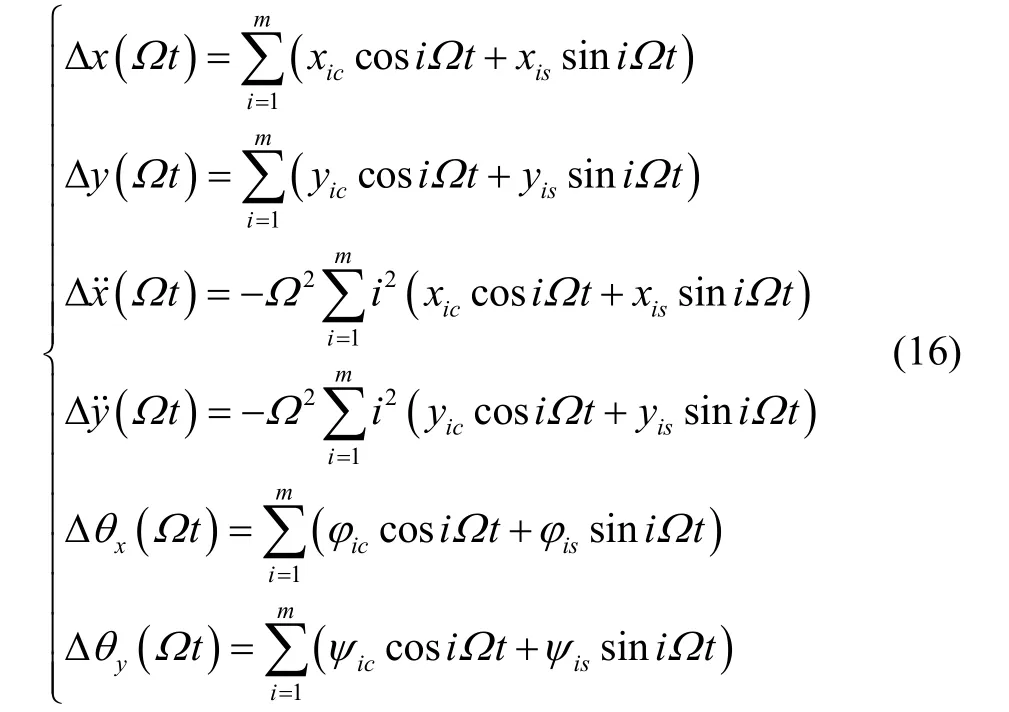
沿旋转平台坐标轴方向等价合成加速度为：

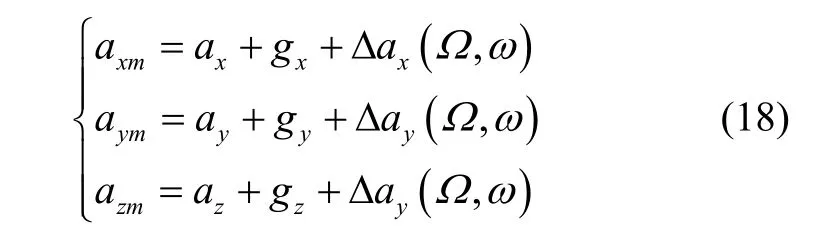
将式(11)(14)代入式(18)得离心机输出加速度为：

带旋转平台在离心机理想情况下的输出应为：

式(20)与式(19)相减得离心机误差为：

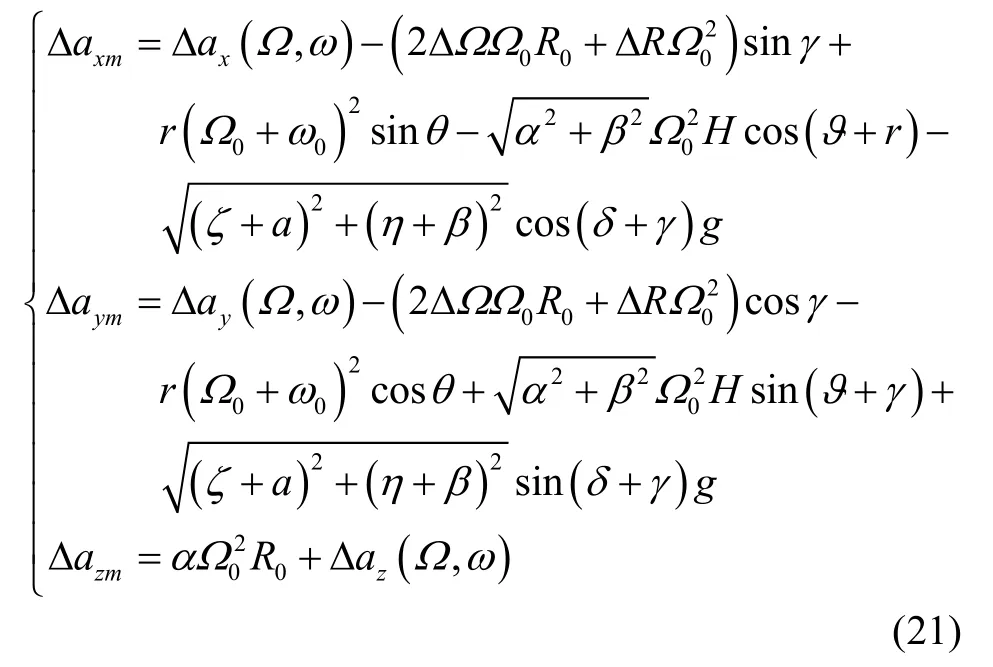
3 加速度计输入误差分析

3.1 考虑加速度计安装误差时的情况

加速度计安装时与旋转平台输出轴之间存在轴系未对准误差，虽然加速度计的安装误差并不是离心机的误差源，但是它对于加速度计误差系数的标定会产生影响，因此仍需考虑。设加速度计输入轴水平偏差角为φ，垂直偏差角为ψ，加速度计坐标轴为MX3Y3Z3，如图 3所示，可以通过OXYZ坐标系平移r并绕MZ3轴旋转φ角然后再绕MY3轴旋转ψ角获得，同样假设φ≤10-4rad，ψ≤10-4rad。

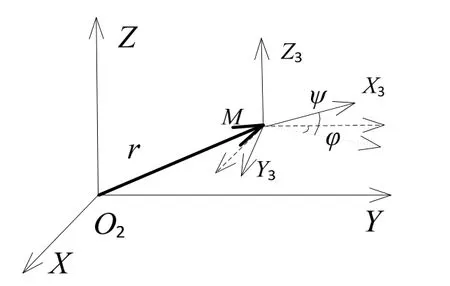
图3 加速度计安装误差Fig.3 installation error of accelerometer

计算加速度在加速度计输入轴、摆轴和输出轴上的投影，同样应用小角度定理进行简化并忽略高阶小项，得加速度计检测比力为：

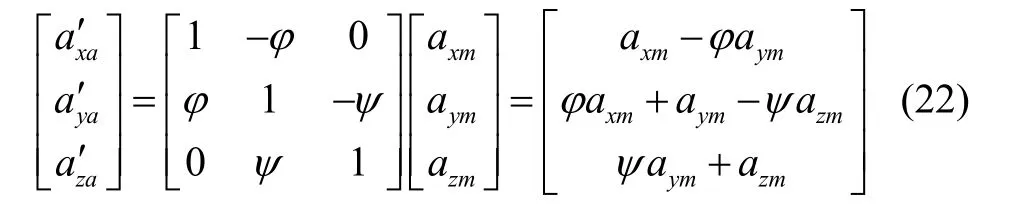
加速度计实际输入值为加速度计敏感到的离心机输出加速度与地球转速产生的牵连运动导致的惯性加速度的和，将惯性加速度加入，并将式(19)代入式(22)得到含离心机误差和加速度计安装误差较完整的加速度计输入比力表达式如式(23)如示：

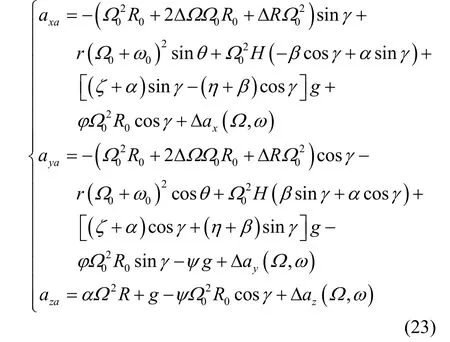
将式(23)与式(20)相减，得沿加速度计三个轴方向的最终加速度检测误差表达式为：

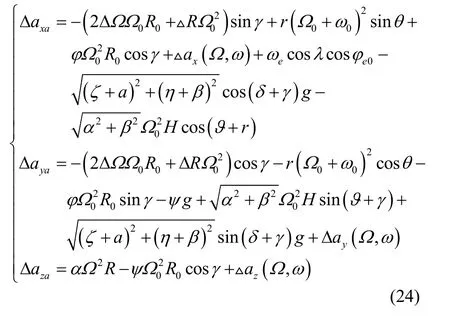
3.2 误差分析

对误差表达式(24)进行分析可得以下结果：

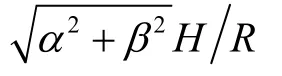
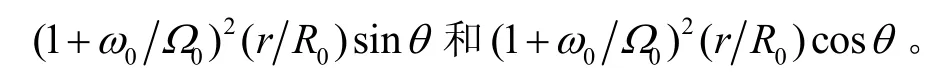
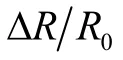
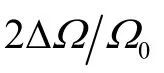
⑥ 加速度计检测轴水平未对准角 φ会给加速度计输入轴和摆轴输入比力带来φ倍误差；垂直未对准角ψ给加速度计摆轴输出比力带来ψg的误差，给输出轴带来ψ倍误差。

⑦ 主轴回转误差给加速度计输入加速度引入与离心机旋转周期相关的谐波误差分量。对谐波误差取时间均值可知，主轴旋转误差会给加速度计输入均值引入常值偏量。仅当旋转平台旋转频率ω取特殊值，如ω= -Ω时，主轴回转误差的均值为0。

⑧ 地球转速产生的牵连运动导致的惯性加速度给加速度计输入引入可补偿的常值误差。

4 结 论

由以上误差分析可知：离心机安装误差主要影响重力加速度；旋转平台安装误差会引入半径不确定性，主要影响离心机输出加速度，并同时影响重力加速度；检测质心偏移r给离心机输出加速度引入恒值直流偏差，当离心机作为线振动测试设备使用时影响较大，需要通过检测仪器反算并补偿，当离心机作为带同步反转平台的离心机使用时对输出无影响；加速度计未对准角会给输入比力引入误差；主轴旋转误差给加速度计输入加速度引入谐波误差分量；地球转速产生的牵连运动导致的惯性加速度给加速度计输入引入常值误差。

以上误差同时影响离心机的输出精度，离心机的总误差为各分项误差之和，在离心机的设计与研制中必须综合考虑各方面因素，合理分配各个误差项，以确保离心机测试能实现预期精度。离心机输出误差也会带来加速度计输入误差，各项误差对加速度计高阶误差系数标定的具体影响研究，以及如何对恒值误差如地球旋转产生的牵连惯性加速度和可测量误差如回转误差、安装误差等进行补偿可以在后续工作中展开。

（References）：

[1] Curey R K. Gyro and accelerometer panel: 50 year of service to the inertial community[J]. Aerospace and Electronic Systems Magazine, 2013, 28(7): 23-29.

[2] 陈才，王毅，郭刚，苏宝库. 惯性导航平台辨识的离心机方法[J]. 电机与控制学报，2010，14(1)：84-89.

CHEN Cai, WANG Yi, GUO Gang, SU Bao-ku. Centrifuge methodology of inertial navigation platform identification[J]. Electric Machines and Control, 2010, 14(1): 84-89.

[3] Neugebauer G H. Precision centrifuge testing of an accelerometer[R]. AD736435, 1971.

[4] 王世明，任顺清，王常虹.在反转平台离心机上标定陀螺仪的误差模型系数的方法[J]. 中国惯性技术学报，2012，20(5)：625-630.

WANG Shi-ming, REN Shun-qing, WANG Chang-hong. Calibration of gyro error model coefficients on precision centrifuge with counter-rotation platform[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 625-630.

[5] IEEE Std 836-2009. IEEE recommended practice for precision centrifuge testing of linear accelerometers[S]. The Institute of Electrical and Electronics Engineers, 2009.

[6] 任顺清，陈岩，赵振昊. 精密离心机主轴回转误差对加速度计输入精度的影响[J]. 中国惯性技术学报，2007，15(1)：116-119.

REN Shun-qing, CHEN Yan, ZHAO Zhen-hao. Influence of rotary errors of centrifuge spindle on accelerometer input accuracy[J]. Journal of Chinese Inertial Technology, 2007, 15(1): 116-119.

[7] 杨业，梁禄扬，吴浩，郭涛. 基于带回转台离心机试验的惯性平台仿真建模研究[J]. 航天控制，2014，32(2)：9-17.

YANG Ye, LIANG Lu-yang, WU Hao, GUO Tao. Inertial platform modeling and simulation based on centrifuge test with a rotation table[J]. Aerospace Control, 2014, 32(2): 9-17.

[8] Su Bao-ku, Chen Cai, Guo Gang. Application of unscented Kalman filter in identification of INS error parameters based on centrifuge test[J]. Journal of Chinese Inertial Technology, 2010, 18(3): 382-386.

[9] Ren Shun-qing, Wang Shi-ming. Impacts of installation errors on the calibration accuracy of gyro accelerometer tested on centrifuge[C]//Proceedings of 2013 2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation. Toronto, Canada, 2013: 914-918.

[10] 姜岩松，刘雨，苏宝库. 正交双加速度计在离心机上的测试方法及模型辨识[J]. 航空精密制造技术，2011，47(1)：15-19.

JIANG Yan-song, LIU Yu, SU Bao-ku. Test method and model identification of dual orthogonal accelerometers on centrifuge[J]. Aviation Precision Manufacturing Technology, 2011, 47(1): 15-19.

精密线振动特性离心机的误差分析

邹仲贤，曾 鸣，刘 雨

Error analysis on centrifuge with precise linear vibration

ZOU Zhong-xian, ZENG Ming, LIU Yu
(Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China)

The precise linear vibration is an effective test method for realizing high-order error calibration, and error analysis is critical for improving the testing accuracy and perfecting testing scheme. In high-precision accelerometer testing, a little equipment error will take significant effects on the results. In this paper, the working principle and the output characteristics of centrifuge with precise linear vibration characterization is presented, the error coordinate system of centrifuge is modeled based on its mechanical structure, and the output acceleration containing errors of centrifuge is calculated by a vector derivation method. Finally, the effects of each non-independent error source on the input acceleration are analyzed in the acceleration coordinate system when the centrifuge generates sinusoidal acceleration, and the results could provide theoretical reference for the accelerometer error compensation.

precise centrifuge; rotation platform; error analysis; linear vibration; overload acceleration

联 系 人：曾鸣（1957—），男，教授，博士生导师。E-mail：zengming@hit.edu.cn

1005-6734(2014)06-0839-06

10.13695/j.cnki.12-1222/o3.2014.06.0026

U666.1

A

2014-07-04；

2014-11-21

总装备部预先研究项目（51309050202）；国家自然科学基金（61203116）

邹仲贤（1985—），女，博士研究生，从事惯性仪表测试及测试设备研究。E-mail：zzx_hit@163.com