基于多模型分段拟合的光纤陀螺温度误差补偿方法

（海军工程大学 电气工程学院，武汉 430033）

（海军工程大学 电气工程学院，武汉 430033）

传统光纤陀螺温度误差采用单一模型进行建模与补偿，存在模型适配性较差的问题。考虑到光纤陀螺在不同温度区间的温度特性存在明显差异，为提高光纤陀螺温度误差补偿精度，提出了基于多模型分段拟合的光纤陀螺温度误差补偿方法。设计了-15～50 ℃区间内温度实验，在大量实测数据分析基础上，将陀螺温度特性按照低、中、高三个温度区间，分别建立三种不同阶次的温度误差模型。采用分段拟合的方法进行误差建模，并利用所建模型对光纤陀螺进行了温度误差补偿。实测数据表明，提出方法能够有效改善光纤陀螺的温度漂移，补偿后漂移标准差减少66.67%。

光纤陀螺；温度漂移；多模型；补偿

近年来光纤陀螺由于其潜在的优势，广泛应用在汽车导航、火箭姿态控制、武器控制等领域，具有广阔而光明的前景[1-3]。相比传统的机械陀螺，光纤陀螺具有精度高、耐冲击、动态范围大、寿命长、对重力加速度不敏感等突出优势[4]。

作为惯性导航系统的核心器件，光纤陀螺对温度敏感性很大，温度漂移成为主要的误差源。当环境温度变化时，陀螺的零位漂移明显加剧，标度因子的线性度也明显变差[5]。因此，对光纤陀螺的温度特性进行研究，并利用温度模型进行补偿以提高陀螺精度是非常有必要的。传统光纤陀螺温度误差补偿方法采用单一模型进行建模与补偿，忽略了光纤陀螺在不同温度区间的温度特性存在明显差异的事实。本文将陀螺温度特性按照低、中、高三个温度区间，分别建立三种不同阶次的温度误差模型，提出了基于多模型分段拟合的光纤陀螺温度误差补偿方法，有效提高了光纤陀螺温度误差补偿精度。

1 温度影响机制分析

陀螺温度场是指陀螺工作环境温度的分布情况，由光纤陀螺器件和外部环境辐射所形成的热环境就是其温度场分布。构成光纤陀螺仪的核心部件对温度敏感，陀螺工作环境温度变化将导致光纤环中光纤折射率发生变化，则两束反向传播的干涉光将产生一个不同的光程差，形成非互易效应[6-7]，最终引起光纤陀螺的零点漂移随温度的变化而不同。

温度对光纤陀螺的影响包括两个方面，一是陀螺工作的环境温度对陀螺工作状态的影响，二是陀螺器件本身材料特性对温度的敏感性。漂移决定了陀螺输出信号的偏移量，工作环境温度变化时，光纤陀螺的偏移量主要是由非互异相移引起的位置偏移。

当两束干涉光分别以顺时针(CW)和逆时针(CCW)方向传输通过长度为L、折射率为n的光纤环时，产生的相位延迟为：

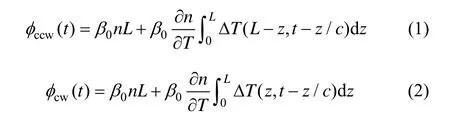
式中，φcw(t)为顺时针光产生的相移，φccw(t)为逆时针光产生的相移，β0= 2π/λ0为光在真空中的传输常数，n为光纤折射率，c为光在光纤环中传播的速度，z为任一点到端点的距离，Δ T 为光纤z点的温度分布变化量[8-9]。化简后得到光纤环温度变化产生的热致非互易相位延迟为：

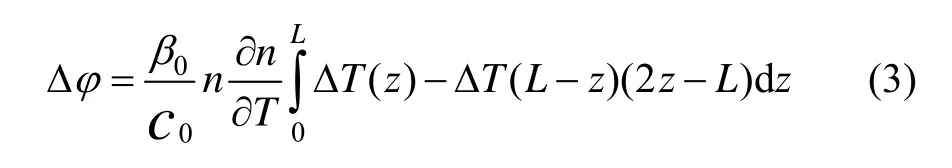
由以上分析可知，光纤陀螺的温度漂移是定量可测的。

2 多模型温度建模及补偿

温度补偿是用软件的方法对陀螺的温度误差进行修正，补偿因温度变化引起的陀螺零漂。因此必须建立相关的温度和漂移模型。依据模型，根据测量得到的温度预测对应的温度漂移值，再用陀螺的实际输出值减去预测值得到补偿后的陀螺输出。

实验时将陀螺置于温箱内，X、Y、Z陀螺的放置方向为前、上、右，每5 ms保存一帧数据。实验测量了-15～50 ℃温度区间变化时的零漂。以X陀螺为例，在得到的陀螺输出中，减去地球自转角速度分量，得到的陀螺漂移如图1所示。

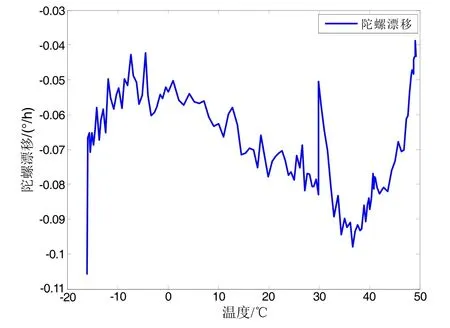
图1 陀螺漂移Fig.1 FOG drift

通过数据分析发现，在不同的温度区间，温度对陀螺漂移的影响效果不同。因此，考虑用分段多模型进行建模。数据分析后发现，在-15～0 ℃范围内，陀螺漂移与温度变化近似成正比形式，在0～30 ℃范围内，陀螺漂移与温度变化近似成反比形式，在30～50 ℃范围内，陀螺漂移与温度变化近似为二次函数关系。

将温度分成以下三个区间：-15～0 ℃；0～30 ℃；30～50 ℃，采用如下的模型通式：

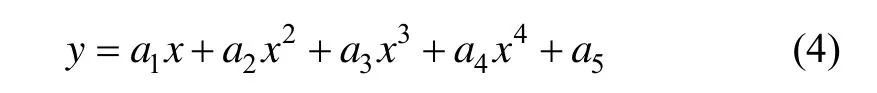
式中，a1、 a2、 a3、 a4、 a5为所建模型的参数，x表示温度，y表示温度漂移。利用最小二乘法分别对各段温度漂移进行建模，分段拟合的效果如图2所示。

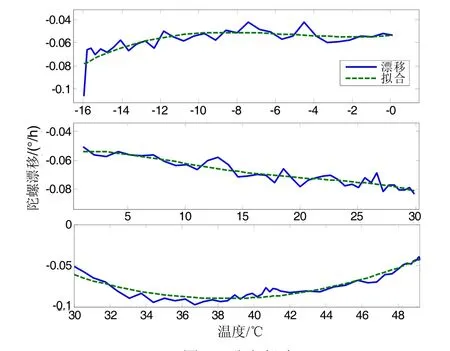
图2 分段拟合Fig.2 Piecewise fitting

可以看出采用的不同模型，都可以很好地拟合各段陀螺漂移。通过处理将各段曲线连接起来，形成完整的温度漂移补偿模型。补偿效果如图3所示。

计算发现，在-15～50 ℃范围内，补偿前最大漂移为 0.106 (°)/h，标准差为 1.465e-2 (°)/h；补偿后最大漂移为0.027 (°)/h，标准差为5.205e-3 (°)/h。相比补偿前，陀螺漂移标准差减少了66.67%，补偿效果明显。

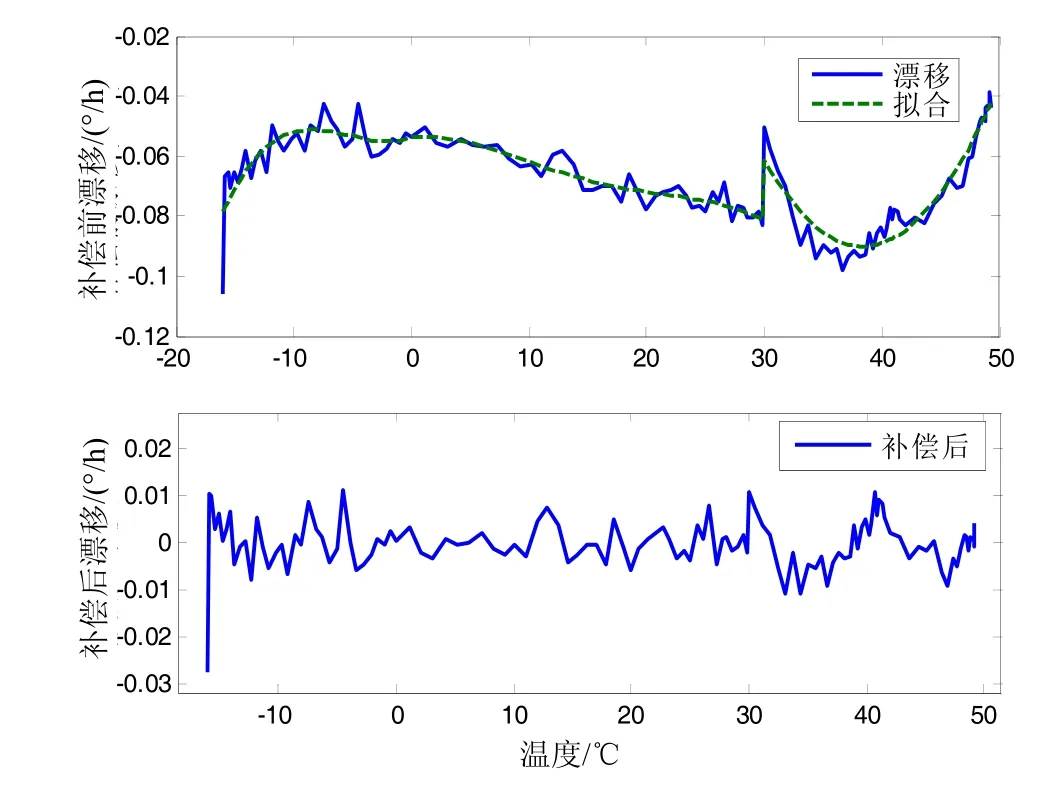
图3 补偿效果Fig.3 The effect of compensation

在实验得到的数据中，分别随机选取三个温度区间段的数据，用所建模型对其进行补偿验证，验证效果如图4所示。

可以看出，对于不同组的温度漂移，利用所建立的模型，仍然具有良好的补偿效果。补偿前最大漂移为0.099 (°)/h，标准差为1.485e-2 (°)/h；补偿后最大漂移为0.012 (°)/h，标准差为4.675e-3 (°)/h，验证了建立的补偿模型的正确性。

本文采用的多模型分段拟合补偿方法与传统的采用单一模型拟合补偿方法比较，具有良好的补偿效果，比较结果见表1。本文采用的分段多模型详细参数见表2。

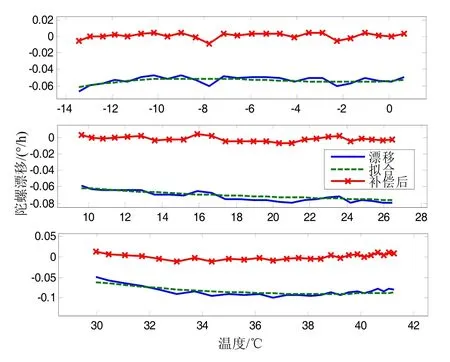
图4 模型验证效果Fig.4 The effect of model

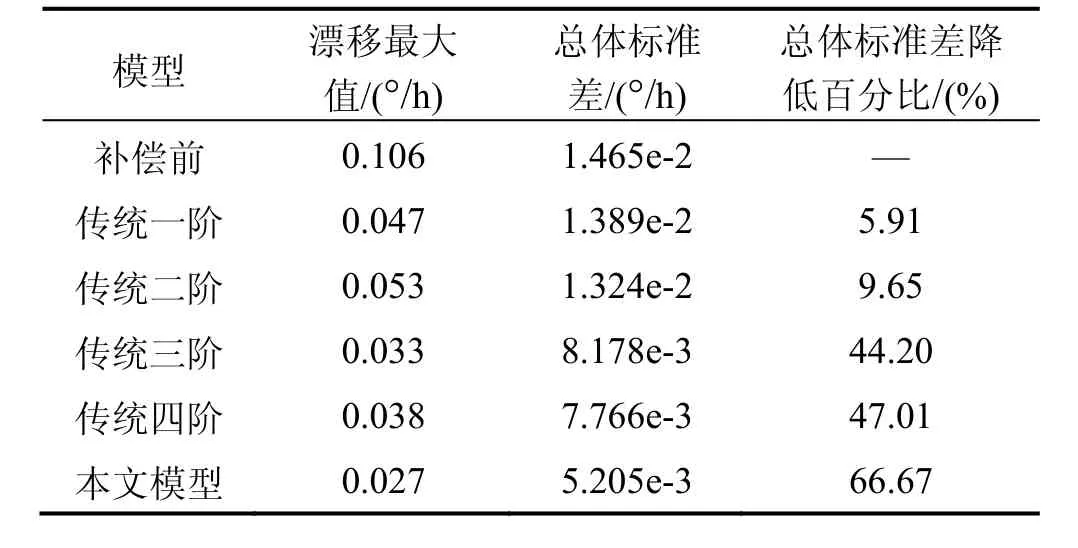
表1 本文方法与传统方法比较Tab.1 Comparison between proposed method and traditional method

表2 模型参数Tab.2 Model parameter

3 结 论

在大量实测数据分析处理基础上，研究了温度对光纤陀螺零漂的影响。研究发现，温度对零漂的影响在不同的温度区间有不同的规律。因此采用分段建模的方法，建立多模型的分段温度漂移模型，并依据模型，对实测数据进行补偿验证。补偿的结果表明，在-15～50 ℃温度区间内，补偿前漂移标准差为 1.465e-2 (°)/h，补偿后漂移标准差降至 5.205e-3 (°)/h，比补偿前减少66.67%，补偿效果明显，方法可行。

从补偿的结果来看，补偿后还留有残余误差，说明未能通过建模补偿的方法完全消除温度漂移。对高精度的光纤陀螺进行建模和补偿时，还需要进一步分析残余的温度漂移，考虑更多的影响因素，建立更加精细的温度漂移模型。

（References）：

[1] Xu X, Zhang C, Pan X. Study of reflection error in closed-loop polarization-maintained interferometric fiber optic gyroscope.[J]. Optik-International Journal for Light and Electron Optics, 2010, 121(13): 1170-1175.

[2] 杨孟兴，陈俊杰. 光纤陀螺静态温度特性的分析及实验研究[J]. 中国惯性技术学报，2011，18(6): 51-755.

YANG Meng-xing, CHEN Jun-jie. Analysis and experiment on static temperature characteristic of FOG[J]. Jour-nal of Chinese Inertial Technology, 2011, 18(6): 751-755.

[3] 程建华，陈李，李明月. 船用光纤陀螺精密温控系统的设计与实现[J]. 中国惯性技术学报，2011，19(4): 403-407.

CHENG Jian-hua, CHEGN Li, LI Ming-yue. Design and realization of precision temperature control system for ship borne FOG[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 403-407.

[4] Xiyuan Chen, Chong Shen. Study on temperature error processing technique for fiber optic gyroscope[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(9): 784-792.

[5] 石国祥，陈拣，叶军，等. 光纤陀螺温度影响的非线性综合误差补偿[J]. 四川兵工学报，2011(3)：76-78.

SHI Guo-xiang, CHEN Jian, YE Jun. Nonlinear error compensation effect of temperature of fiber optic gyro[J]. Journal of Sichuan Ordnance, 2011(3): 76-78.

[6] 李传生，张春熹，王夏霄，等. Sagnac型光纤电流互感器变比温度误差分析与补偿[J]. 电力自动化设备，2012，32(11)：102-106, 114.

[7] LI Chuan-sheng, ZHANG Chun-xi, WANG Xia-xiao, et al. Analysis and compensation of ratio temperature error for sagnac fiber-optic current transformer[J]. Electric Power Automation Equipment, 2012, 32(11): 102-106,114.

[8] Corporation H P. Analysis and optimization of dynamic measurement precision of fiber optic gyroscope[J]. Mathe- matical Problems in Engineering, 2013, 2013(2):142-148.

[9] Jie-yu L, Jian-ye Y, Li-xin W, et al. Error autocompensation of FOG-based rotating inertial measurement unit for ballistic missile[J]. Opto-Electronic Engineering, 2012, 39(6):41-46.

[10] Wang J, Liu Y, Fan W. Design and calibration for a smart inertial measurement unit for autonomous helicopters using MEMS sensors[C]//Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation. 2006: 956-961.

基于多模型分段拟合的光纤陀螺温度误差补偿方法

冯卡力，李 安，覃方君

Temperature error compensation method for FOG based on multi-model piecewise fitting

FENG Ka-li, LI An, QIN Fang-jun
(Electrical Engineering College, Naval University of Engineering, Wuhan 430033, China)

Traditional fiber optic gyro (FOG) uses a single model to model and compensate its temperature error, resulting the problems of poor model matching. In order to improve the temperature error compensation precision, a temperature error compensation method based on multi-model piecewise fitting is proposed by taking into account the different temperature characteristics in different temperature range of FOG. Temperature test is designed and implemented in -15～50℃. After analyzing a large amount of measured data, three temperature error models with different orders are established respectively according to low, medium and high temperature range. By using the piecewise fitting method to model, the temperature errors can be compensated based on the established models. Experimental data show that the proposed method can effectively reduce the FOG temperature drift, and the standard deviation of temperature drift is reduced by 66.67% after compensation.

fiber optic gyro; temperature drift; multi-model; compensation

1005-6734(2014)06-0825-04

10.13695/j.cnki.12-1222/o3.2014.06.023

U666.1

A

2014-07-12；

2014-11-13

国家自然科学基金资助项目（61104184，41404002）；总装预研基金（JB11124，JB11378）；海军工程大学自然科学基金（JJ13011）

冯卡力（1991—），男，博士研究生，从事导航、制导与控制研究。E-mail：fengkali@126.com

联 系 人：覃方君（1979—），男，讲师。E-mail：haig2005@126.com