一种新的二进制偏移载波调制信号无模糊度捕获算法
2014-10-21华东交通大学信息工程学院南昌330013
(华东交通大学 信息工程学院,南昌 330013)
(华东交通大学 信息工程学院,南昌 330013)
二进制偏移载波 (BOC,Binary Offset Carrier) 调制有效地解决了导航信号间的相互干扰,实现了频谱资源的有效利用。针对BOC信号的自相关函数在±1码片内存在多个正负峰,易造成误捕旁峰和漏捕信号的风险,通过分析了 BOC信号中单个码片内调制的矩形脉冲之间的周期延拓关系,确定一个基准单元,将BOC信号可分离成基准单元和基准单元经一系列周期延拓后相加,基于此实现BOC信号自相关函数的分离。根据对称性,可重构一个峰值较低单峰,基于产生的单峰与 BOC信号自相关函数相乘即可消除多峰并提高中心主峰峰值。BOCs(2,1)、BOCs(3,2)和BOCc(2,1)信号仿真结果表明,该方法能完全消除信号的旁峰,适用于任意阶数的正弦或余弦相位BOC信号的捕获,而且保留了BOC信号窄相关峰特性,峰宽度为1/k个码片。
BOC调制;多峰性;周期延拓;分离重构;窄相关性
目前卫星导航由单GPS时代进入GNSS时代,由于频谱资源有限,导致系统内和系统间的干扰。BOC调制方式[1]是以方波作为副载波对伪随机码进行预调制,使得信号频谱对称分裂于频带边缘,以减少信号间的相互干扰。然而BOC信号的自相关函数在±1chip内存在多峰性,捕获中具有两方面的问题:一是误捕到旁峰造成捕获模糊度,从而影响测距精度;二是存在多个零点导致漏捕信号,从而延长了捕获搜索时间。消除上述问题的主要方法有:① 多载波模型 BPSK like法[2],它将BOC信号看成无穷多个BPSK信号的叠加,本地产生等价的载波同时剥离主载波和副载波,积分后相关峰为一个类似于BPSK信号的单峰,该算法有 0.5~0.8 dB的能量损失;② 副载波相位消除法(SCPC,Subcarrier Phase Cancellation)[3],它是借鉴了主载波剥离的思想,本地产生两路副载波相位正交的BOC信号,将BOC、QBOC码互相关函数和BOC码自相关函数平方相加将得到的不含零点的相关曲线,该方法消除了漏捕问题,但没有保留 BOC信号窄相关峰特性;③ 自相关边锋消除法(ASPeCT,Autocorrelation Side- peak Cancellation Technique)[4],它利用了BOC(n,n)信号自相关函数和BOC(n,n)/PRN的互相关函数在相同码相位处具有类似的旁峰特点,通过增加权值系数,研究表明处理后的旁峰与主峰的峰值比达到 9.5%,此算法仅适用于 BOC(n,n)信号,且旁峰消除的并不完全。
本文基于BOC信号中每个扩频码片内调制的方波脉冲的周期性,每个码片内取第1个矩形脉冲组成新副载波并调制扩频码为一个基准单元,BOC信号可以看作是基准单元和基准单元经一系列周期延拓后的相加,从而 BOC信号自相关函数分离成这一系列基准单元与 BOC信号的互相关函数的累加。根据对称性,找出一对互相关函数来可重构一个峰值较低单峰,基于产生的单峰与 BOC信号自相关函数相乘即可消除多峰并提高中心主峰峰值。该方法既保留的 BOC信号窄相关峰特性,同时适用于任意阶数的正弦或余弦相位的BOC信号捕获。
1 相关函数分离重构原理
BOC调制是以方波作为副载波对伪随机码进行预调制,根据方波相位分别记为BOCs(m,n)和BOCc (m,n),其中m是副载波频率 fsc与基准频率 f0的比值,n是伪码速率 fc与基准频率 f0比值。调制阶数k=2m/n,表示单个码片内半个副载波周期数。输入信号表示为:

式中,c(t)为伪随机码,s c(t)为正弦相位副载波,D (t)为导航电文比特,ωIF为中频载波频率,φ ( t)为初始载波相位, Ps为输入信号功率, n(t)为白噪声。 c(t)、 sc(t)如式(2)和式(3)所示:

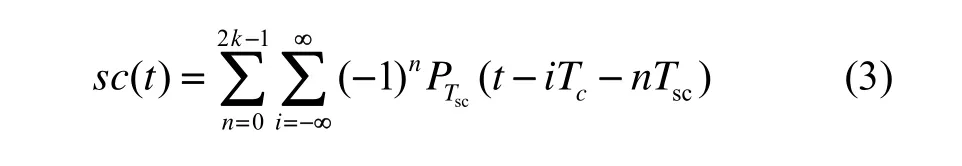
式(2)中 PTc(t)是周期为 Tc的矩形脉冲, Tc是一个伪码码片周期, ci是第i个码片的符号, ci∈(- 1,1);式(3)中 PTsc(t)是周期为 Tsc的矩形脉冲, Tsc是半个副载波周期。图1为信号频谱特性对比图,BOC(6,1)信号频谱主瓣对称分裂,充分利用了频谱资源。图2为信号自相关特性对比图,BOC(6,1)信号自相关函数存在多峰性,在±1码片内的峰数为2k-1,各峰编号l依次为0,1,2…11,各峰值为(- 1)l(k - |l| )/k[5]。随着k值的增大,旁峰与主峰的峰值逐渐接近,误捕的风险进一步提升,而零点个数增加,漏捕的风险亦随之增大[6]。

图1 信号频谱对比图Fig.1 signal Spectrum comparison
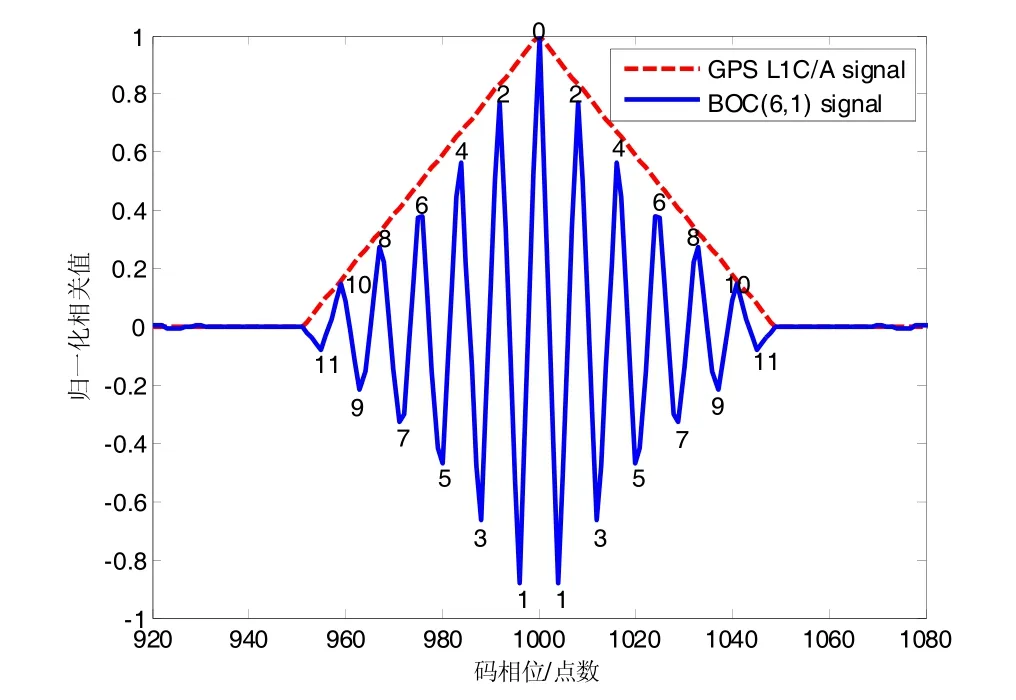
图2 信号自相关函数对比图Fig.2 Signal’s autocorrelation function comparison
1.1 相关函数的分离
BOCs(m, n)信号中每个伪码码片由k个矩形脉冲调制(脉冲宽度为Tsc),单个伪码码片内调制的矩形脉冲之间存在周期延拓的关系,即以第1个矩形脉冲为基准,将剩余的 k-1个矩形脉冲看作是第1个矩形脉冲的周期延拓,符号与之相同或相反。SCF(t)表示每个扩频码片内取第1个矩形脉冲而组成的新的副载波,那么每个扩频码片内取第j个矩形脉冲组成的副载波表示成SCj(t),如式(4)所示:

即SCj(t)相当于SCF(t)往右平移(j-1)Tsc。当j为偶数时,SCj(t)与SCF(t)符号相反;当j为奇数时,SCj(t)与SCF(t)符号相同。伪码经SCF(t)调制产生的信号,记为BOCF(t),将BOCF(t)看作一个基准单元,如式(5)所示:

式(6)表示为完整的BOCs(m, n)信号,它看作基准单元和基准单元经一系列周期延拓后的相加。研究表明,若表示为 BOCF(t)与 BOC(t)的互相关函数,BOCs(m,n)信号自相关函数R(τ )可分离成RF(τ )与RF(τ )延迟后的累加,如式(7)所示:

1.2 相关函数的重构
定义每一个扩频码片内取第k个矩形脉冲组成的副载波为SCL(t),它由SCF(t)向后时延T=(k-1)Tsc得到。伪码经SCL(t)调制产生信号为BOCL(t),它可由基准单元表示,如式(8)所示:
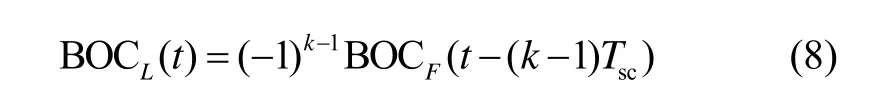
若RL(τ )表示为BOCL(t)与BOC(t)信号的互相关函数,则式(7)中第 j= k- 1项即为式(9):

BOCL(t)与 BOCF(t)存在式(8)所描述周期延拓的关系,所以RL(τ )可由RF(τ )往右平移(k-1)Tsc得到。当k偶数阶时,RL(τ )与RF(τ )符号相反;当k为奇数阶时,RL(τ )与RF(τ )符号相同。图3为以BOC(6,1)信号为例,RF(τ )、RL(τ )的相关函数图,它们关于码相位τ = 1000对称。利用该对称性[10],可通过重构相关函数就能够产生一个峰值较低的单峰。

∧ (τ)是一个宽度为1/k个码片的三角峰,式(10)中重构单峰的峰值相当于 BOCs(m,n)信号自相关函数主峰峰值的2/k,重构的单峰与BOCs(m,n)信号自相关函数相乘即可消除多峰并提高中心主峰峰值。BOC信号的自相关函数如式(12)所示:

图3 相关函数RF(τ )和RL(τ )Fig.3 correlation function RF(τ )and RL(τ )
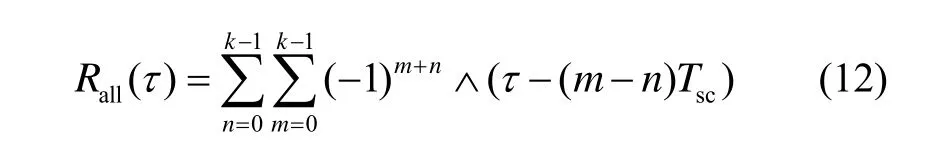
将式(11)与式(12)相乘,结果如式(13)所示:

若 sc(t)为余弦相位的副载波,即对于BOCc(m,n)信号,一个扩频码片调制有2k个矩形脉冲(矩形脉冲宽度为Tsc/2),由上述分离原理得到 RF(τ),而相应的RL(τ)可由 RF(τ)延迟调整 T = (k - 0.5)Tsc,符号调整为(-1)k,通过RF(τ )、RL(τ )及Rall(τ )可重构得到BOCc(m,n)信号无旁峰的相关函数。
2 基于相关函数分离重构捕获算法
综合上述原理的分析,基于相关函数分离重构捕获的原理图如图4所示。
以I路为例,输入信号XIF(t)经主载波剥离后,本地伪码经副载波SCF(t)、SCall(t) (SCall(t)为完整副载波)调制产生两路本地BOC信号,与输入BOC信号相乘,经积分后的输出值如式(14)、式(15)所示:

由于 RL(τ )和 RF(τ )存在式(9)的关系,IF延迟T= (k - 1)Tsc,然后乘以(-1)k-1调整相关函数的符号得到IL路输出值如式(16)所示:
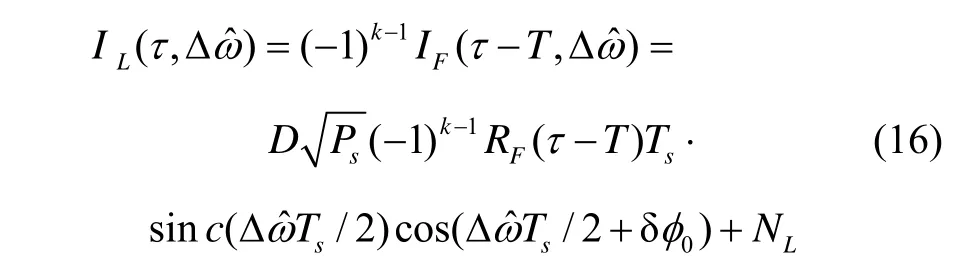

图4 基于相关函数分离重构捕获原理图Fig.4 The acquisition principle based on correlation function separate and reconstruction
由式(14)和式(16)得到IF、IL经过图4虚线框中重构相关函数的过程,将得到的输出值Icomb如式(17)所示:

式中, Ncomb为经重构后的高斯白噪声,均值等于0,方差等于σ2。重构后的 Icomb(τ, Δ与 Iall_l( τ, Δ)取模相乘,然后进行M段非相干累加即可得到I路的输出值YI,同理可得到Q路输出值YQ,如式(18)(19)所示:
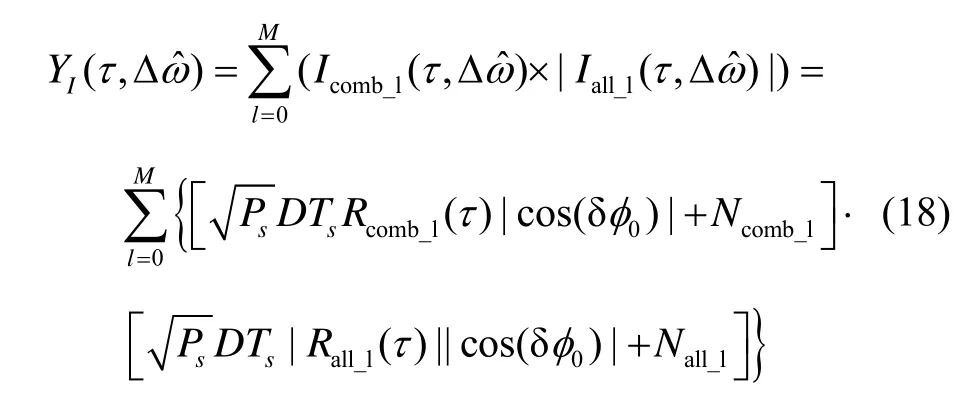

图4所示最终的检测量:

3 检测统计量及性能评估
在相干积分Ts内,IL路值由IF路值的延迟T得到,NL与NF、Nall为不相关的高斯白噪声,均值等于0,方差[7]等于σ2。为了分析方便先假设 Δω ˆ= 0,以I路为例说明,将式(16)整理得到纯信号项:

纯噪声项:

信号与噪声交叉项:

不考虑导航数据位跳变,D为常量可以省去,Ncomb_1与Nall_1为不相关的高斯白噪声,v =Ncomb_l×Nall_l服从正态乘积分布(normal product distribution),v的概率密度函数如式(25)所示:

式中, Kn(·)为第二类 n阶修正贝塞尔函数, Γ(·)为伽玛函数,则v的方差如下:

根据中心极限定理,纯噪声项V服从类似高斯分布[10],其方差:

信号与噪声的交叉项的方差:

综上YI、YQ服从高斯分布,均值如式(30)(31)所示:

YI、YQ的方差如式(32)(33)所示:
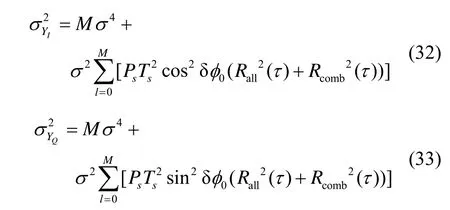
因此η是服从均值等于mη,方差的高斯分布:
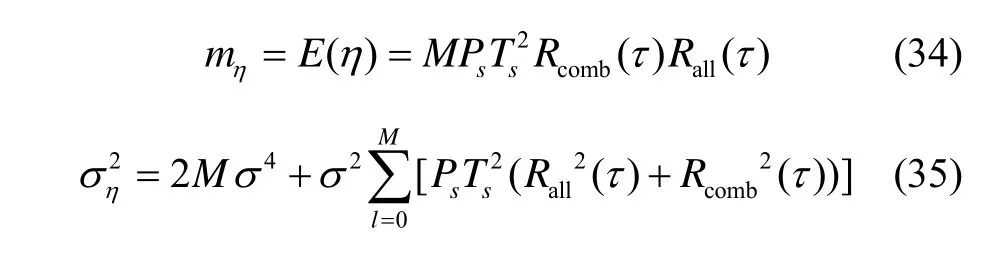
在假设 H0下,即只对噪声进行处理,检测量 Z为均值为0,方差为2Mσ4高斯变量的平方,服从中心χ2分布,其概率密度函数如下:

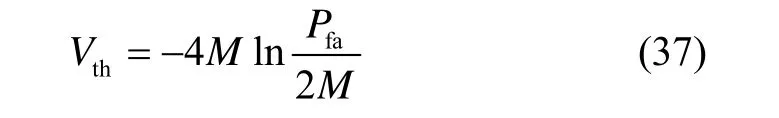
在假设 H1下,对信号叠加噪声进行处理,检测量Z是均值为mη,方差为高斯变量的平方,检测量Z服从非中心χ2分布,其概率密度函数为:

与传统信号捕获的检测性能影响因素不同,BOC信号的检测性能由噪声和旁峰共同影响。假设虚警概率Pfa=0.01,相干积分时间Ts=1 ms,图5为分离重构法、ASPeCT、SCPC、BPSK Like法捕获BOC(n,n)类信号主峰的检测概率随输入信号载噪比变化的关系。在相同码相位捕获精度的前提下,分离重构法、ASPeCT的检测概率明显优于SCPC、BPSK Like法,原因是前两种方法保留了 BOC(n,n)类信号窄相关峰特性。如图 6所示,k=2时,分离重构法、ASPeCT处理后的峰宽度为0.5个码片,而SCPC和BPSK Like法处理后的相关峰宽度为2个码片[10]。在相同载噪比条件下,噪声更容易使得经SCPC和BPSK Like法处理后相关值在±0.5码片范围外超过捕获门限,从而降低捕获性能。
从图5中可知,分离重构法的性能优于ASPeCT,由于经 ASPeCT处理后的旁峰依然存在,峰峰比为9.5%,在±0.5码片范围外超过捕获门限,降低了捕获性能。若以90%的检测概率为标准,ASPeCT捕获到中心主峰的性能相比分离重构法低1.8 dB·Hz。BPSK Like法的检测性能低于SCPC法0.6 dB·Hz,其原因是BPSK Like法通过独立处理BOC信号主瓣达到消除旁峰的目的,存在0.5~0.8 dB的能量损失,而SCPC则没有这样的能量损失。

图5 检测概率与载噪比的关系Fig.5 Detection probability vs. carrier to noise ratio

图6 相关主峰宽度与调制阶数的关系Fig.6 Relationship between correlation main-peak width and modulation order
4 实验结果分析

图7 BOCs(2,1)信号捕获结果Fig.7 Result of BOCs(2,1) signal’s acquisition
基于 Matlab平台实现对相关函数分离重构捕获算法验证,并对比分析了它与其他主流算法的性能。输入信号的相关参数为:中频fIF=4.309 MHz,多普勒fd=1000 Hz,码相位τ=1000采样点,信噪比为-23 dB。采样频率fs=32 MHz,预检积分时间为1 ms,多普勒搜索范围为±5 kHz,频率搜索步径为500 Hz。分别以BOCs(2,1)、BOCs(3,2)及BOCc(2,1)信号为目标捕获源来验证分离重构法、ASPeCT法、SCPC法及BPSK like法,图 7(a)、8(a)、9(a)分别为分离重构法对于这三类信号的三维捕获结果图,捕获得到的码相位、多普勒频率等于预设值。为了对比分析多峰性消除效果,图7(b)、8(b)、9(b)给出了四种捕获算法二维捕获结果对比图。
上述仿真结果表明,相关函数分离重构法、SCPC法、BPSK Like法均能消除三类BOC信号的多峰性,但后两者没有保留 BOC信号的窄相关峰特性,得到检测峰宽度为2个码片,不满足BOC信号高精度捕获要求。捕获搜索中采用最大相关值作为检测量,除了BPSK like法捕获的码相位出现1、4个采样点偏差之外,其他方法捕获的码相位和多普勒频率均与实验前设定的参数一致。ASPeCT法对于 BOCs(2,1)、 BOCs(3,2)、BOCc(2,1)信号处理后的峰峰比分别为55.3%、33.3%、53.4%。若降低捕获门限,多峰性引起的捕获模糊度的问题依然存在,即算法已经失效,而基于相关函数分离重构的方法是利用码片内调制的矩形脉冲之间存在周期延拓的关系为理论出发点,突破了副载波相位类型和调制阶数奇偶性的限制,对于BOCs(m,n)类信号(k为偶数阶)、BOCs(m,n)类信号(k为奇数阶)、BOCc(m,n)类信号(k为偶数阶)仍然适用,拓宽了算法的适用性,并且保留了BOC信号窄相关峰特性。

图9 BOCc(2,1)信号捕获结果Fig.9 Results of BOCc(2,1) signal’s acquisition
5 结 论
BOC调制技术有效利用了频谱资源而被应用于卫星导航定位系统上,但其自相关函数多峰性使得传统捕获技术带来信号的误捕和漏捕。目前研究的BOC信号的捕获方法的适应性差,而且没有利用的 BOC信号窄相关的特性。本文研究了 BOC调制的每个扩频码片内方波脉冲之间的关系,提出一种适用于任意阶数的 BOC信号的捕获算法。仿真结果表明,该算法能够有效消除任意阶数的正弦或余弦相位 BOC信号的自相关函数旁峰,并突破了副载波相位类型和调制阶数奇偶性的限制,同时能够保留了 BOC信号的窄相关峰特性,检测峰宽度为1/k个码片。
(References):
[1] Betz J W. Binary offset carrier modulations for radio navigation[J]. Navigation: Journal of the Institute of Navigation, 2001, 48(4): 227-246.
[2] Yang L, Jiapin C, Zhenbo L, et al. A second order BPSK-like (SOB) method for the acquisition of BOC(1,1) [C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation. Fort Worth, 2007: 1073-1078.
[3] Yang Z, Huang Z, Geng S. unambiguous acquisition performance analysis of boc (m, n) signal[C]//IEEE International Conference on Information Engineering and Computer Science. 2009: 1-4.
[4] Julien O, Macabiau C, Cannon M E, et al. ASPeCT: unambiguous sine-BOC(n,n) acquisition/tracking technique for navigation applications[J]. Transactions on Aerospace and Electronic Systems, 2007, 43(1): 150-162.
[5] 何在民. BOC信号的相关器设计及跟踪性能分析[D].西安:中国科学院国家授时中心,2008.
HE Zai-min. The correlator design of BOC and tracking performance analysis[D]. Xi’an: National Time Service Center, Chinese Academy of Sciences, 2008: 34-50.
[6] 徐启炳,宋志强,王登峰,等. 新型导航信号的捕获方法研究[C]//第二届中国卫星导航学术年会. 上海:2011. XU Qi-bing, SONG Zhi-qiang, WANG Deng-feng, et al. Research on acquisition methods of new navigation signals[C]//The Second China Satellite Navigation Academic Annual Meeting. Shanghai: 2011: 1-5
[7] 杨静,刘一霏. 基于GPU的GPS信号并行捕获[J]. 中国惯性技术学报,2012,20(4):430-434.
YANG Jing, LIU Yi-fei. Parallel-acquisition of GPS signa l based on graphic processing unit[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 430-434.
[8] Kim S, Chong D, Yoon S. A new GNSS synchronization scheme[C]//Vehicular Technology Conference. Barcelona, 2009: 1-4.
[9] Schmid A, Neubauer A. Differential correlation for GALILEO/GPS receivers[C]//Acoustics, Speech, and Signal Processing International Conference. Philadelphia, 2005: 953-956.
[10] Wang H, Ji Y, Shi H, et al. The performance analysis of unambiguous acquisition methods for BOC(m,n) modulated signals[C]//Wireless Communications Networking and Mobile Computing 7th International Conference. Shanghai: 2011: 1-4.
一种新的二进制偏移载波调制信号无模糊度捕获算法
胡 辉,李 林,雷明东,路 春
New unambiguous acquisition algorithm for binary offset carrier modulated signal
HU Hui, LI Lin, LEI Ming-dong, LU Chun
(College of Information Engineering, East China Jiaotong University, Nanchang 330013, China)
Binary offset carrier(BOC) modulation can effectively solve the mutual interference between navigation signals, and realize the effective use of spectrum resources. However, BOC signal′s autocorrelation function has multiple positive and negative peaks within ±1chip, which leads to error acquisition and lost acquisition. To solve this problem, the periodic extension among the modulated rectangular pulses in each spread spectrum code chip are analyzed, and a base unit is determined to separate the BOC signals into a base unit and a combined unit which superimposed a series of periodic extended base units, and thus realize the separation of BOC signal’s autocorrelation function. According to the symmetry, a low single correlation function is reconstructed, which can not only remove side peak, but also increase the value of center main peak by means of single peak multiplied with BOC single’s autocorrelation function. The results show that the proposed method can remove side-peaks of BOCs(2,1), BOCs(3,2), and BOCc(2,1) signal, and therefore can be applied to any order of sine or cosine phase BOC signal acquisition. Moreover, it reserves BOC signal’s the features of narrow correlation peak, and the width is 1/k chip.
BOC modulation; multi-peaks; periodic extension; separation reconstruction; narrow correlation
E-mail:hu_hui@ecjtu.jx.cn
1005-6734(2014)06-0763-07
10.13695/j.cnki.12-1222/o3.2014.06.012
TN961
A
2014-07-14;
2014-11-05
国家自然科学基金资助项目(61162015)
胡辉(1970—),男,博士,教授,从事卫星导航定位研究、并行算法与并行处理、机器人视觉。
