基于卡尔曼滤波的再入飞行器气动参数辨识

（1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.北京宇航系统工程研究所，北京 100076）

（1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.北京宇航系统工程研究所，北京 100076）

再入飞行器的制导系统易受气动参数扰动的影响，为此研究气动参数在线辨识方法可以为再入制导系统提供服务，有效提高制导的精度。以卡尔曼滤波理论作为基础，推导了再入飞行器气动参数辨识的数学模型。为增强卡尔曼滤波方法对气动参数的辨识效果，气动参数误差模型采用一阶高斯马尔科夫过程描述，并增广到状态方程组中，根据获得的带有测量误差的惯导信息，对气动参数进行估计。最后，进行了数学仿真研究。仿真结果表明，该方法都能够在10个采样周期内收敛，且估计精度在1%以内。

气动参数辨识；卡尔曼滤波；一阶马尔科夫；再入飞行器；惯导设备

由于地面风洞试验不够准确或气动计算预先估计的气动特性与实际飞行过程中的气动特性存在差异，导致再入飞行器性能有所下降。解决这个问题方法有：①采用先进的制导方法，以增强再入制导系统的鲁棒性，使其能够适用于气动参数不确定性对其造成的影响[1]；②利用飞行器上惯导的量测数据和弹载计算机，实时地辨识出飞行中的气动参数，并补偿控制信号，达到精确控制的目的[2]。由于受制导、控制系统及飞行器本身的约束限制，方法①在一定范围内比较适用。随着现代飞行器和电子技术的高速发展，方法②受到了越来越多的关注，对提高再入飞行器的性能提升具有重要的现实意义。

用于参数辨识方法有递推最小二乘法、递推极大似然法、卡尔曼滤波等，其中卡尔曼滤波方法应用最为广泛。为增强辨识效果，随后出现了多种参数辨识方法，包括扩展卡尔曼滤波EKF、不敏卡尔曼滤波UKF[3]以及强跟踪滤波STF[4]。基于卡尔曼滤波的在线气动参数辨识方法最早出现于战斗毁伤自修复的飞行控制系统中，但是卡尔曼滤波器要求参数变化规律已知，这对气动参数估计并不奏效。因此，基于卡尔曼滤波的气动参数辨识方法需要建立合适的参数变化规律模型。

文献[5]基于EKF方法对再入机动目标进行跟踪，文献[7]基于 UKF对多个机动目标进行跟踪，均取得了较好的跟踪效果。本文利用类似文献[5]的思想，将待辨识的气动参数视为“目标机动”，其变化规律采用一阶高斯马尔科夫过程及噪声补偿技术来描述，并将它们增广到状态方程组中，然后根据获得的带有测量误差的加表信息对再入飞行器的气动参数进行估计。仿真结果表明该方法能够很好地跟踪时变参数的变化趋势，同时提高了参数辨识效果。

本文的主要工作安排如下：首先对再入飞行器气动辨识问题进行描述；然后基于纵平面简化的动力学模型，建立了气动参数的不确定性模型和惯导的量测模型，并给出了滤波算法；最后进行了数学仿真研究。

1 问题描述

再入飞行器的标准气动数据由地面风洞试验获得，然后将气动数据装订到弹载计算上，根据当前特征参数（再入飞行器的气动数据一般是攻角和马赫数的函数），通过在线插值或拟合计算得到。但是在实际飞行过程中，由于风洞试验数据不够准确或者受到当时气象因素的影响，导致预先装订的数据与实际的气动数据存在一定差异。

根据标准气动数据，本文建立再入飞行器的气动模型为：

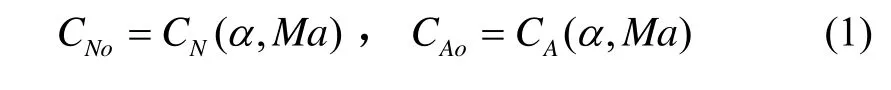
式中，α为攻角，Ma为飞行马赫数， CNo为法向气动参数， CAo轴向气动参数。

在实际飞行过程中，法向气动参数 CNf与轴向气动参数 CAf满足关系：

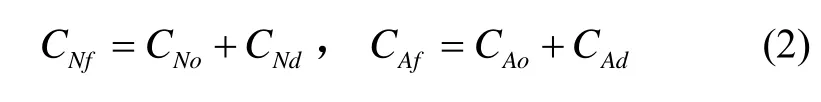
式中， CNd与 CAd为相应气动参数的扰动量，本文主要研究工作是采用卡尔曼滤波算法对其进行辨识。

2 再入飞行器动力学模型

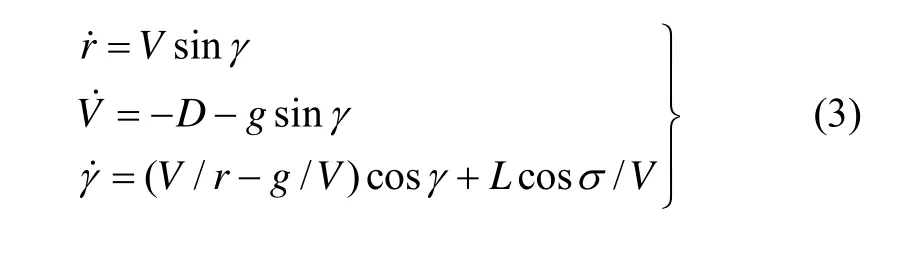
假设地球为不旋转的均质圆球，无动力滑翔再入飞行器在再入飞行过程中仅受到气动力与地球引力的作用，在速度坐标系下纵平面简化动力学模型为：式中，r为飞行器质心到地心的距离，V为飞行器相对地球的飞行速度，γ为飞行路径角，g为地球的引力加速度；σ为倾侧角，是再入飞行过程中的控制量；L为升力加速度，D为阻力加速度，攻角α隐含其中，再入飞行过程中，攻角是事先设定好的攻角剖面，通过姿态控制进行保持。

3 气动参数辨识建模

3.1 系统方程

再入飞行器动力学模型(3)建立在速度坐标系下，而气动数据是在飞行器体坐标下给出的，所以需要进行坐标系变换：

提取式(3)中气动参数相关项，存在气动参数偏差的动力学模型表示为：

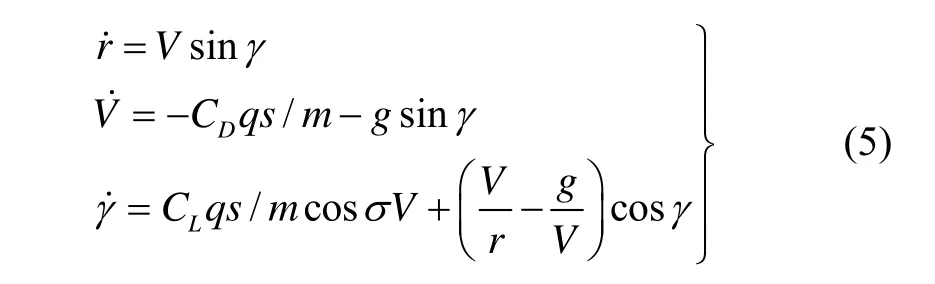
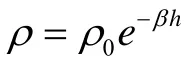
CNd与 CAd描述的是在标准气动数据基础上的气动参数的扰动量，本文将其视为标准数据的“机动”，采用一阶高斯马尔科夫过程进行描述，其具体形式为：

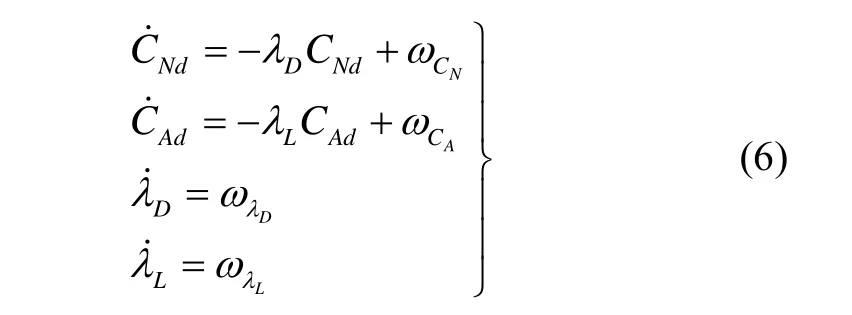
记增广状态变量x为：

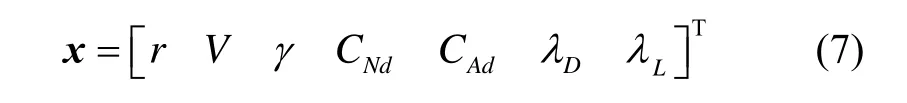
根据式(5)(6)，得到增广后的气动参数辨识系统方程：

式中，ω为系统噪声向量。

3.2 量测方程

对于携带惯性敏感元器件的再入飞行器，可以测量到飞行器体系下除去地球引力的加速度信息，即再入飞行器可以测量到由气动力引起的轴向加速度 Db和法向加速度的 Lb。所以，量测方程为：

式中，y为加速度计的测量数据，ν为加速度计的常值漂移；η为加速度计的随机漂移，服从高斯分布。

4 滤波算法

根据扩展卡尔曼滤波算法原理以及上面给出的系统方程和量测方程，在 [tk,tk+1]采样周期内，设计扩展卡尔曼滤波估计器。

1）状态变量时间更新方程为：

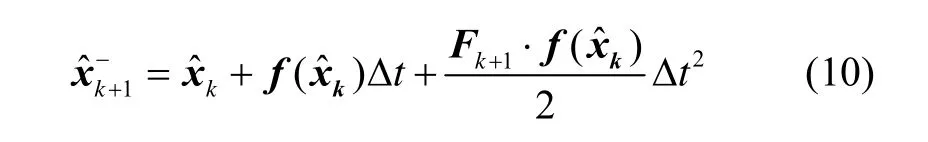
式中，Δ t= tk+1- tk为滤波步长，Fk+1为状态方程 f()对状态量估计值的雅克比矩阵。

2）状态误差协方差矩阵的时间更新方程为：

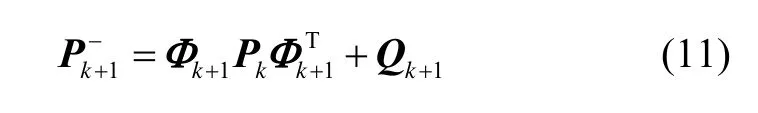
式中， Qk+1为系统过程噪声方差阵， Φk+1为状态转移矩阵，表达为：

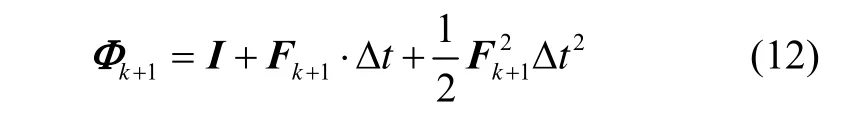
式中，I为单位矩阵。

3）卡尔曼滤波增益更新方程为：

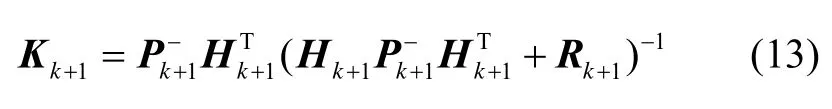
式中， Rk+1为量测噪声矩阵，令 Rk+1=R0， Hk+1为量测方程 h()对状态变量的雅克比矩阵。

4）状态误差协方差矩阵的量测更新为：

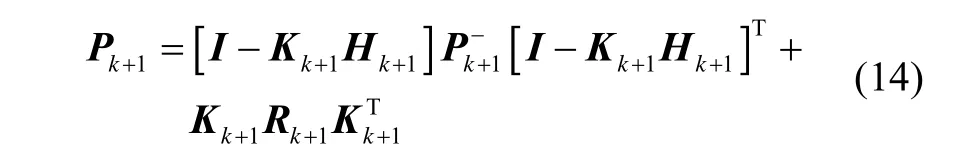
5）量测修正量更新方程为：

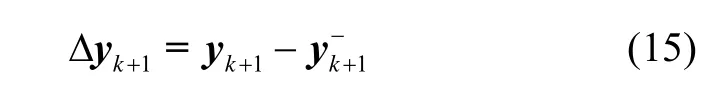
式中， yk+1为 tk+1时刻的观测量，是根据预测的观测量。

6）状态变量更新方程为：

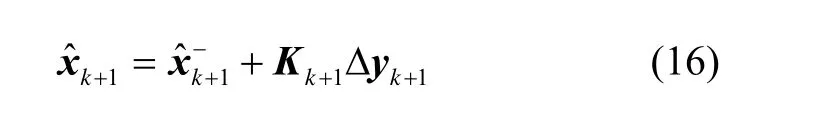
5 数学仿真

5.1 仿真条件

为了验证本文算法对再入飞行器气动参数辨识的有效性，选取某升力式再入飞行器进行研究[6]。再入飞行器的质量为 m=1300 kg，特征参考面积为s=1.677 m2，再入飞行器的标准气动数据是攻角与马赫数的函数。

在滤波算法中，为简化计算假设加速度计仅存在随机漂移项，取其均方差为0.1%，则量测噪声方差矩阵为：

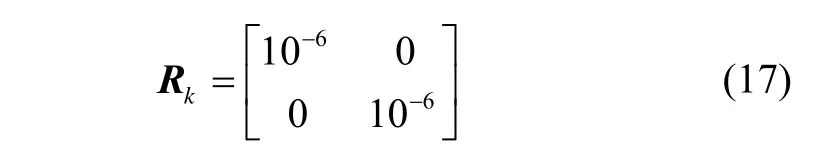
过程噪声方差阵取为：

根据滤波状态初值，状态误差协方差矩阵的初值取为：

5.2 仿真算例1

在标准气动数据的基础上，设定法向气动参数的扰动量 CNd=-0 .2，轴向气动参数的扰动量 CAd= 0.2，均为常值干扰，滤波器采样周期为1 s；然后采用本文提出的方法对它们进行辨识。图1～图2示出了的辨识结果曲线。从仿真结果可以看出：本文提出的辨识方法能够在5～7个采样周期内得到估计结果，收敛速度快，且辨识精度高，误差在1%以内。

5.3 仿真算例2

为验证本文算法的对气动参数辨识的鲁棒性能，人为选取再入飞行器气动参数的扰动量是时间t的三角函数，其具体形式为：

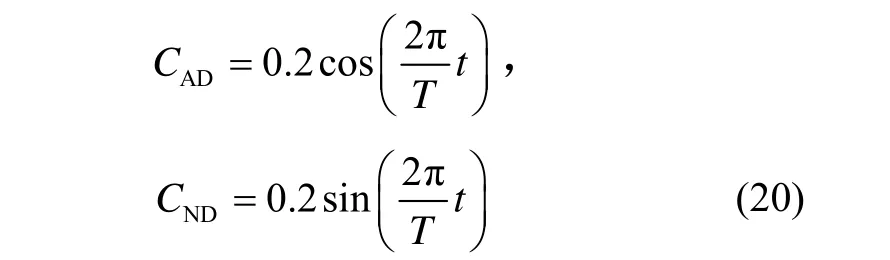
式中，T为三角函数的震荡周期，其它仿真条件均不变。图3～图4示出了的辨识结果曲线。从仿真结果可以看出：在气动参数的扰动量的变化规律较为复杂的情况下，该辨识方法能够在 8～10个采样周期内获得良好的估计结果，且辨识误差在1%以内。

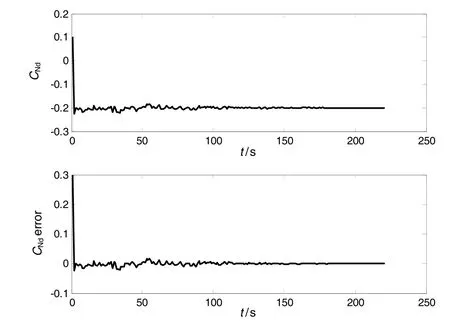
图1 算例1中气动参数 C Nd的辨识结果Fig.1 The identification results of aerodynamic parameter C Ndf or case 1

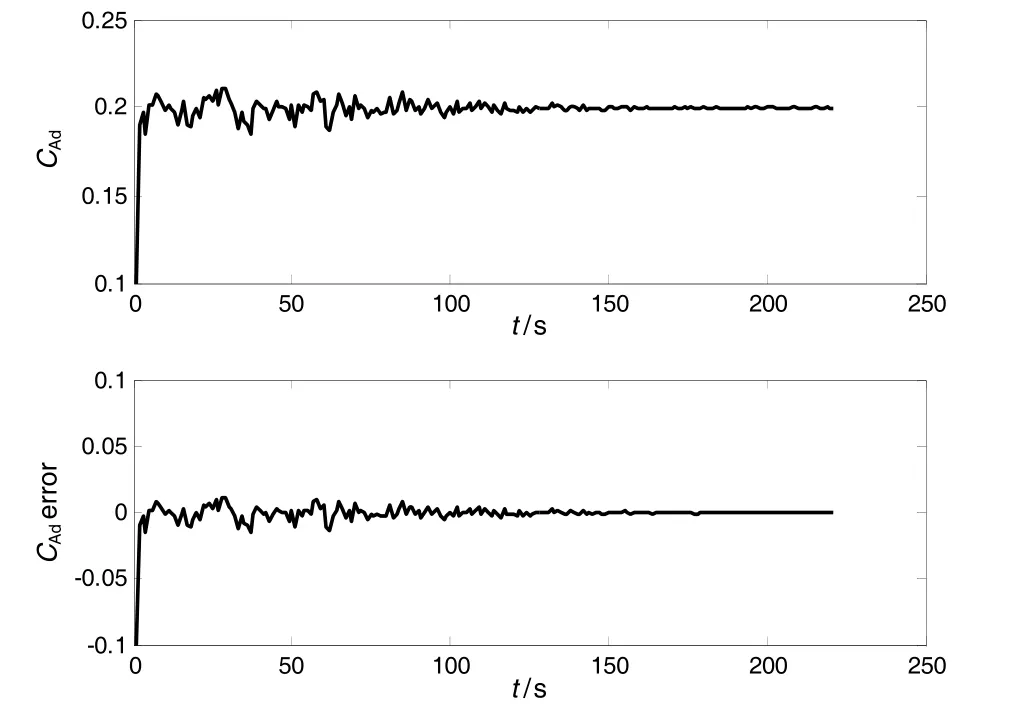
图2 算例1中气动参数 C Ad的辨识结果Fig.2 The identification results of aerodynamic parameter C Adf or case 1

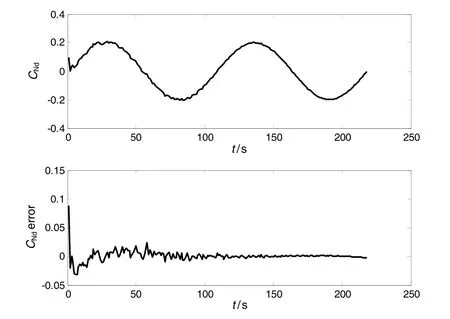
图3 算例2中气动参数 C Nd的辨识结果Fig.3 The identification results of aerodynamic parameter C Ndf or case 2

图4 算例2中气动参数 C Ad的辨识结果Fig.4 The identification results of aerodynamic parameter C Adf or case 2

6 结 论

本文根据再入飞行器动力学模型及其气动模型，建立了再入飞行器气动参数辨识的系统方程与观测方程，采用一阶高斯马尔科夫过程及噪声补偿技术对未知的气动参数的扰动进行描述。在此基础上，利用卡尔曼算法分别对再入飞行器气动参数的常值形式扰动与三角函数形式扰动进行了研究。仿真结果表明，该算法能够准确、快速地完成参数辨识，说明了该算法具有很强的适应性与鲁棒性，具备在线应用的潜力，能够为再入飞行器的制导系统提供实时而准确的气动参数的估值。这为新型再入制导方法的研究开辟了新的视野，是本文下一步的工作内容。

（References）：

[1] XUE Song-bai, LU Ping. Constrained predictor-corrector entry guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1273-1281.

[2] 梁子璇，任章. 基于在线气动参数修正的预测制导方法[EB/OL]. [2012-12-06]http://www.cnki.net/kcms/detail/ 11.2625.V.20121206.1733.005.html.

LIANG Zi-xuan, REN Zhang. Predictive reentry guidance based on dynamic parameter online correction[EB/OL]. [2012-12-06]http://www.cnki.net/kcms/detail/11.2625.V. 20121206.1733.005.html.

[3] Kandepu R, Foss B, Imsland L. Applying the unscented kalman filter for nonlinear state estimation[J]. Journal of Process Control, 2008, 18: 753-768.

[4] Jwo D J, Wang S H. Adaptive fuzzy strong tracking extended kalman filtering for GPS navigation[J]. IEEE Sensors Journal, 2007, 7(5): 778-789.

[5] 崔乃刚，林晓辉，奚敏. 雷达对再入机动目标跟踪算法研究[J]. 宇航学报，1998，19(1)：21-27.

CUI Nai-gang, LIN Xiao-hui, XI Min. The research of radar tracking algorithm to reentry maneuvering target[J]. Journal of Astronautics, 1998, 19(1): 21-27.

[6] 傅瑜. 升力式天地往返飞行器自主制导方法研究[D].哈尔滨：哈尔滨工业大学，2012. FU Yu. Autonomous guidance method for lift transporta- tion vehicle[D]. Harbin: Harbin Institute of Technology, 2012.

[7] WU Pan-long, JI Cun-hui, ZHANG Lian-zheng. Passive multiple maneuvering targets tracking using TDOA measurements[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 609-614.

基于卡尔曼滤波的再入飞行器气动参数辨识

崔乃刚1，卢宝刚1，傅 瑜2，张 旭1

Aerodynamic parameter identification of a reentry vehicle based on Kalman filter method

CUI Nai-gang1, LU Bao-gang1, FU Yu2, ZHANG Xu1
(1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)

The guidance system of a reentry vehicle is vulnerable to the perturbation of the aerodynamic parameter. In this paper, an online identification method for aerodynamic parameter is studied to provide services for the guidance system and improve the guidance precision. The mathematical model of aerodynamic parameter identification is deduced based on Kalman filter theory. In order to improve the effect, an error model of aerodynamic parameter is described by using a first-order Gauss-Markov process and is augmented into the state equations. Based on these, a Kalman filter is used to estimate the aerodynamic parameters by using the obtained inertial navigation information with measurement errors. Finally, the simulations are performed, which show that the proposed method can realize convergence within 10 sampling period, and the estimate error is within 1%.

aerodynamic parameter identification; Kalman filter; first-order Markov; reentry vehicle; inertial equipment

1005-6734(2014)06-0755-04

10.13695/j.cnki.12-1222/o3.2014.06.010

V412.4+4

A

2014-07-27；

2014-11-20

中央高校基本科研业务费专项资金资助（HIT.NSRIF.2015037）

崔乃刚（1965—），男，教授，博士生导师。E-mail：Cui_Naigang@163.com