一种小卫星高精度自主定轨/定姿一体化新方法

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3. 哈尔滨工业大学 航天学院，哈尔滨 150001）

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3. 哈尔滨工业大学 航天学院，哈尔滨 150001）

基于传统小卫星对轨道和姿态参数确定采用分别计算的复杂模式，提出了一种利用地磁场和天文信息同时确定卫星轨道和姿态参数的新方法。首先通过分析小卫星轨道动力学 J2模型和卫星姿态动力学模型，建立系统状态方程。其次将三轴磁强计与地磁场模型参考值的矢量作差，分析微分差值与状态变量的数学关系，建立定位/定姿观测方程。利用星敏感器提供的高精度姿态信息，建立定姿观测方程，同时利用星敏感器间接敏感地平观测折射恒星，建立定位观测方程。最后提出基于信息融合的先进滤波算法，并通过对多种导航模式进行数值仿真及结果分析，论证所设计一体化方法提高了系统定轨/定姿的精度和可靠性。

三轴磁强计；天文导航；轨道姿态一体化；信息融合

随着载人航天、探月技术以及深空探测技术的发展，对航天器自主导航能力的要求也更加迫切，数字化、小型化、全自动化和多功能化已经成为自主导航系统的发展趋势[1-3]。卫星自主导航技术即仅依靠星载设备和技术实时在轨为卫星提供精确轨道及姿态参数，它不仅是卫星自主性的一个重要方面，而且对于卫星在轨生存能力及扩展其在空间应用能力都具有重要的理论意义和应用价值[4]。

1898年美国Cornell大学研究学者首次提出利用地磁场进行自主导航的概念以来，地磁场导航逐渐成为导航领域的新研究领域之一[5]。Bar-Itzhack等提出了利用磁强计测量地磁场实现近地探测器自主导航的方法[6]。Pasiaki等以卫星MAGSAT、DE-2和LACE的真实地磁场矢量模为观测值，分别利用最小二乘方法和扩展卡尔曼滤波修正地磁场模型误差和确定卫星轨道参数，并对算法性能进行评估[7-8]。Deutschmann利用卫星ERBS和GRE真实地磁场矢量为观测值，设计基于扩展 Kalman滤波的卫星自主导航方案得到卫星轨道信息[6,9]。近年来利用地球物理特征的无源自主导航方法重新激起了国内外学者的研究热情，国内对地磁场自主导航研究较晚[10]，王鹏提出了近地微小卫星的磁测自主导航方法[11]，赵敏华[12]、高长生[13]和王淑一[14]等人研究了利用 EKF和 UKF算法进行地磁场定位。

星敏感器是高精度的姿态敏感设备，利用星光折射间接敏感地平天文导航方法是20世纪70年代初发展起来的一种新颖的近地低成本航天器自主天文导航定位方案，其利用高精度星敏感器和大气对星光折射的数学模型及误差补偿方法精确敏感地平，从而实现航天器的精度定位[3-4]。实验研究的结果表明，这种导航系统能够达到定位精度100 m(1σ)、速度精度0.1 m/s(3σ)的较高导航精度，但由于折射导航星个数有限，并且观测时间较短，所以不能连续、长时间地提供观测信息。

本文探索基于地磁场和天文的小卫星轨道和姿态一体化确定方法，推导一体化系统的状态模型和观测模型，提出基于信息融合的先进滤波算法，旨在通过一体化手段充分利用现有星上资源，实现敏感器功能扩展和资源共享，提高小卫星定位和定姿精度和可靠性，降低卫星成本和重量，为我国实施小卫星航天工程奠定理论基础和技术支持。

1 符号说明

本文涉及到的多种符号说明如下：

① 坐标系及坐标系转换

i 为地心惯性坐标系；b 为卫星本体坐标系；o为卫星轨道坐标系；e 为地磁场球面坐标系；p为星敏感器像平面坐标系；为坐标系x转换至y的姿态转换矩阵；q为卫星姿态四元数的真实值；

② 变量说明

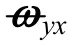
^为变量或矩阵的估计值；Δ为变量或矩阵误差；⊗为四元数乘法；()-1为矩阵求逆或四元数求反；()×为矢量反对称矩阵；δ为微分算子；In×n为n阶单位矩阵。

2 卫星自主定轨/定姿状态方程

2.1 卫星轨道状态方程

① 轨道动力学模型

选取历元(J2000.0)地心赤道惯性坐标系，则通常选用的卫星轨道动力学模型为：

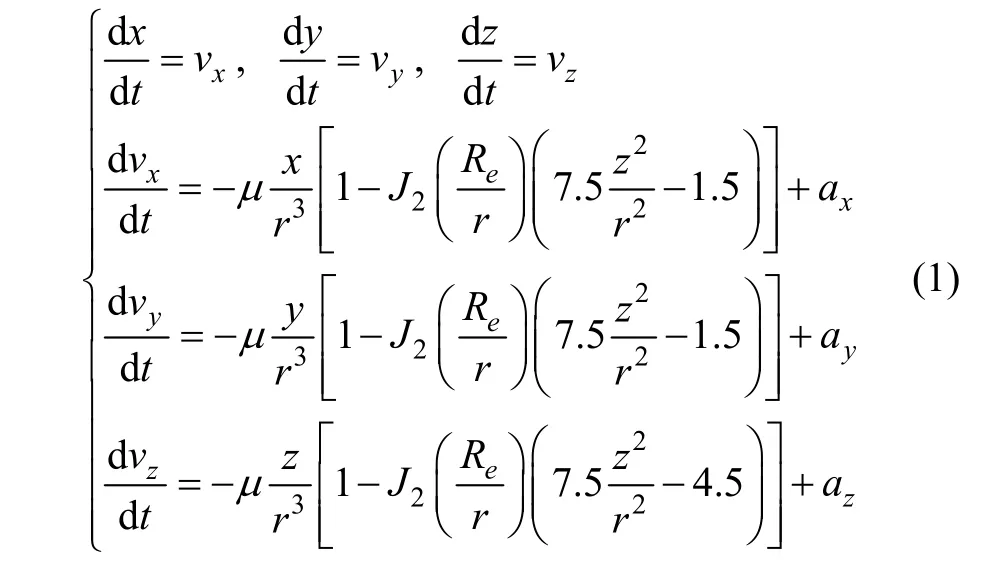
式中，anonspherical是地球非球形摄动加速度，a3-body(sun)和 a3-body(moon)是太阳和月球摄动加速度， aairdrag是大气阻力摄动加速度， aSRP是太阳光压摄动加速度。② 轨道状态方程

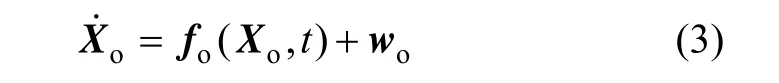
式中， w (t)为系统噪声矢量。

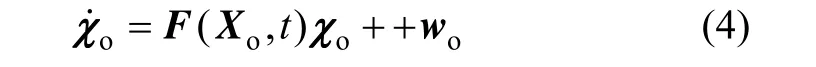
2.2 卫星姿态状态方程

① Δq表达式

定义姿态四元数误差Δq为：

对式(5)两变同时求导，可得：

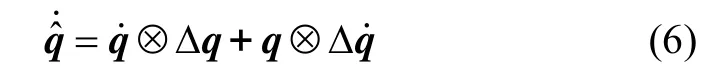
将式(6)两边乘以 q-1，整理可得：

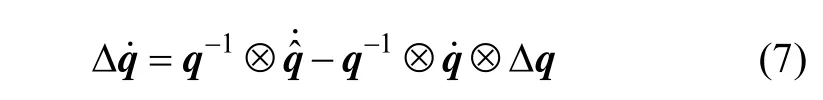
定义卫星角速度估计值 ωˆob为：

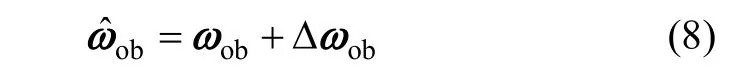
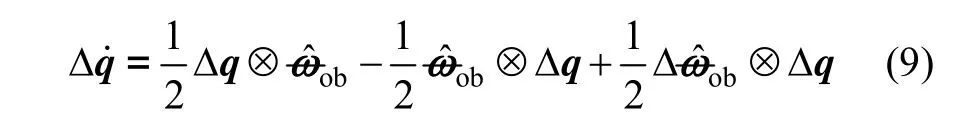
由于姿态四元素的不独立性，将导致误差方差阵的奇异，为了避免滤波过程中的误差协方差矩阵的奇异，需对其进行降维处理。

当Δq为小量时，有 Δq4≈1，忽略高阶小量，化简式(9)，矢量部分Δq可得：

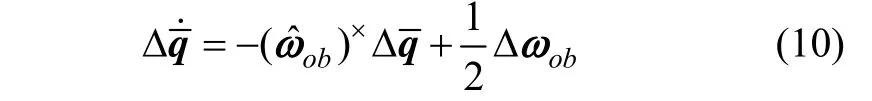
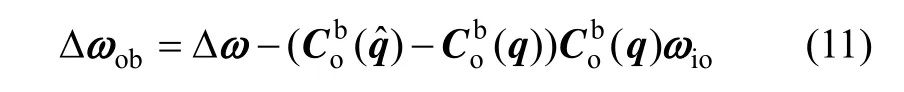
由式(5)，四元数转换矩阵关系为：

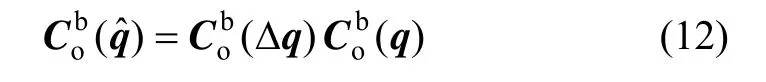
将式(12)代入式(11)可得：

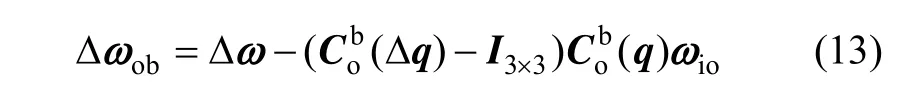
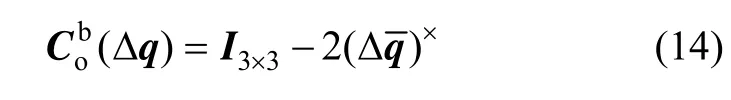
将式(14)代入式(13)，可得：

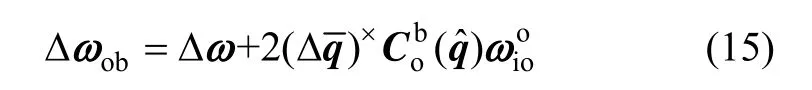
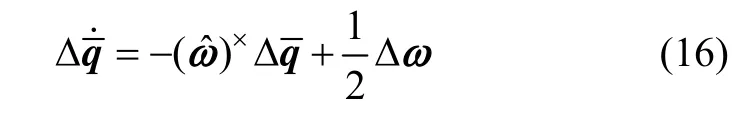
设卫星姿态控制外力矩 Tw=0，则姿态动力学方程可表示为：

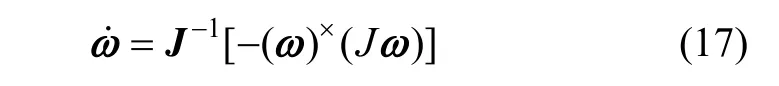
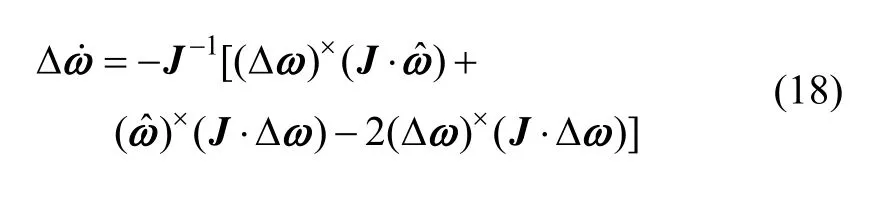
③ 姿态状态方程

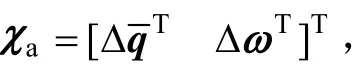
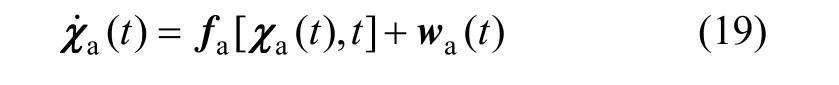
式中， wa(t)为系统噪声矢量。

2.3 卫星轨道/姿态状态方程

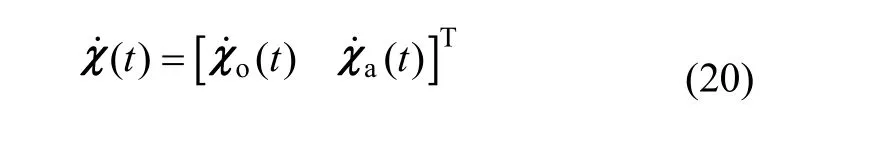
3 卫星自主定轨/定姿状态方程

3.1 地磁场导航

3.1.1 地磁场导航原理

1919年成立的国际地磁学与高空大气物理学协会主要是进行地磁学和高空大气学方面的国际合作与研究，该协会成立专门研究部门每隔5年公布一个新国际地磁参考场，使其得到不断的修正与完善[8]。地磁场数学模型描述采用球谐波模型，地磁场势函数V可表示为：

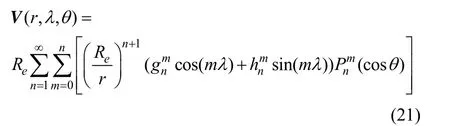
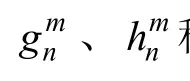
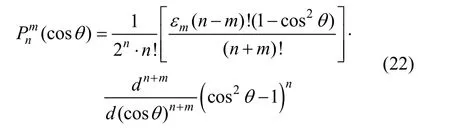
地磁场在纬度、经度和径向三个方向上的偏导数即为地磁场在这三个方向的分量可表示为：

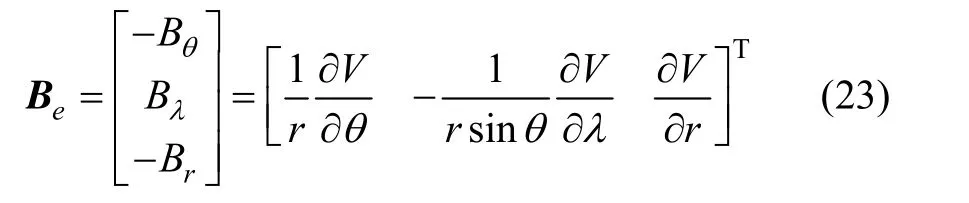
地磁场矢量 Be在地磁场球面坐标系 e与地心惯性坐标系i中的关系可表示为：

3.1.2 地磁场观测方程

根据式(24)，三轴磁强计测量方程可表示为：

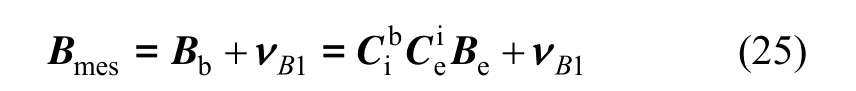
根据国际地磁参考场(IGRF)模型，地磁场矢量估计方程可表示为：

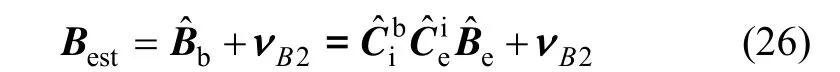
定义磁强计测量值 Bmes与国际地磁参考场估计值 Best误差ΔB为：

将式(25)和式(26)代入式(27)，则地磁场误差观测方程可表示为：

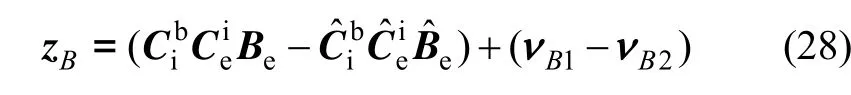
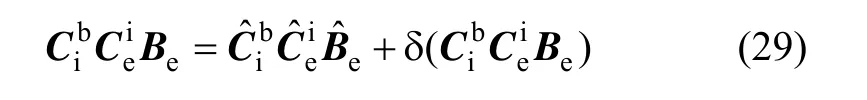
将式(29)代入式(28)，可得：

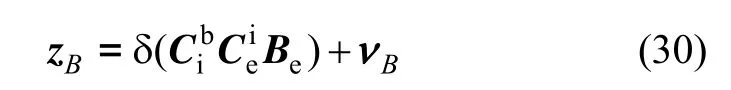
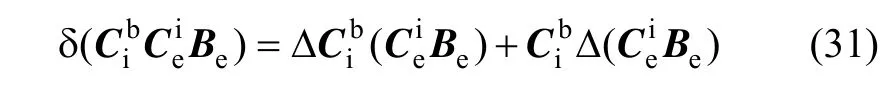
将式(31)代入式(30)，可得：

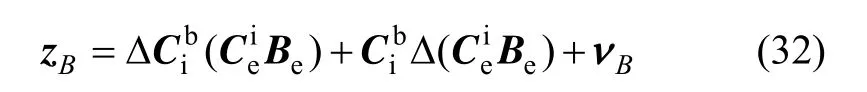
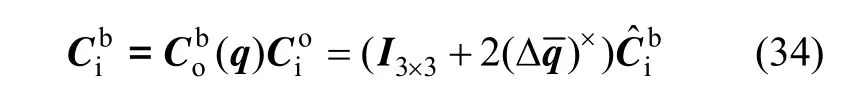
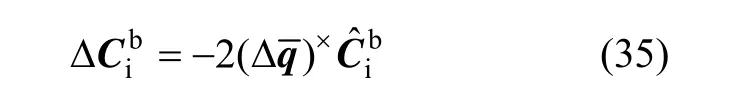
将式(35)代入式(32)右边第一项，即可得：

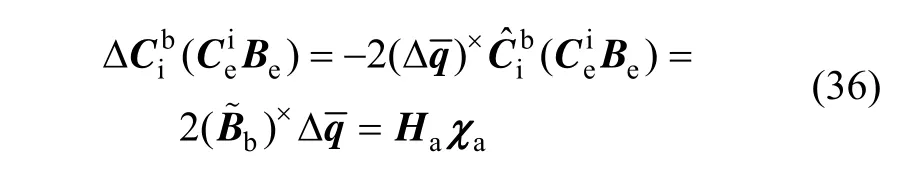
根据微分定义，式(31)右边第二项可表示为：

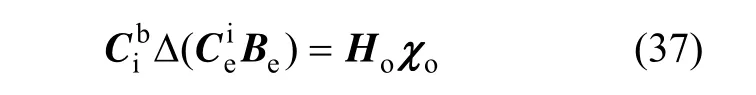
综合式(36)(37)，则三轴磁强计观测方程可写为：

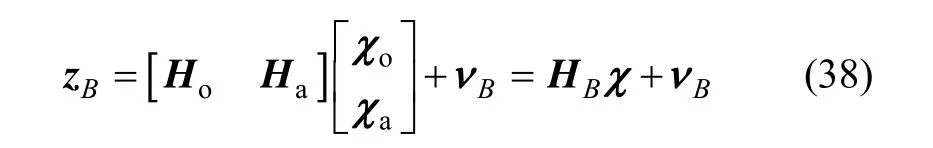
3.2 星敏感器姿态确定

3.2.1 星敏感器测量原理

星敏感器以恒星作为姿态测量的参考源，可输出恒星在星敏感器坐标下的矢量方向，为航天器的姿态确定提供高精度测量数据。安装在三轴稳定卫星上的星敏感器由光学系统和面阵光敏元器件组成，来自星光的平行光经过光学系统，在面阵上聚焦成像圈。在星敏感器像平面坐标系 p中，XpYp沿面阵的正交基准，Zp轴沿中心光轴，(x0, y0)和(xj, yj)分别是Zp轴和星光在XpYp平面上的坐标，f为光学系统的焦距。星光矢量在敏感器坐标系中的方向为：

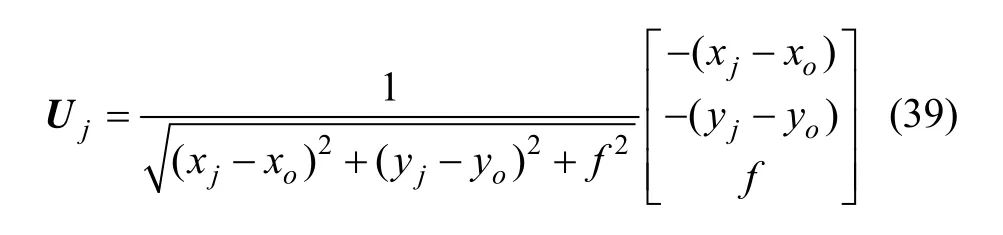
由于星敏感器像平面坐标系p与航天器本体坐标系 b的姿态矩阵是可知的，所以可以得到在航天器本体坐标系b中恒星星光方向矢量 Sb：

3.2.2 星敏感器观测方程

在地心惯性坐标系 i中，由于恒星的张角非常小，经过长期天文观测，它们在惯性空间中的方位是精确已知的，恒星星表能够提供高精度的惯性参考基准。恒星星光方向矢量在航天器本体坐标系b中的测量值 Ss可表示为：

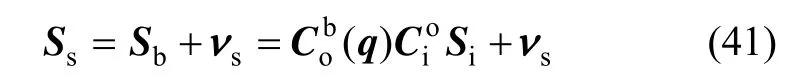
式中， Si可由星历表给出。

将式(12)和式(13)代入式(41)，化简可得：

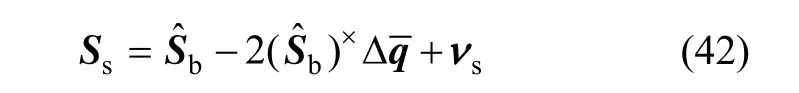
设有两个星光矢量确定卫星姿态，由式(42)，星敏感器观测方程可表示为：

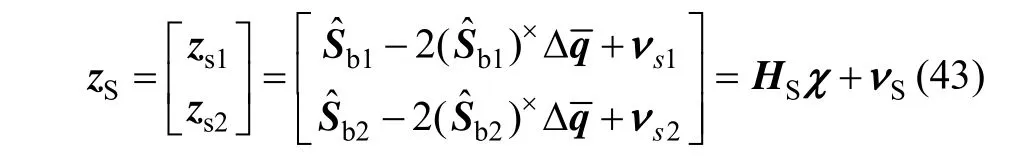
3.3 间接敏感地平

3.3.1 导航原理

间接敏感地平是利用星敏感器测量恒星星光在通过地球边缘大气层时所发生的折射间接得到地平信息，由此确定轨道参数的一种自主导航方法。卫星、地球和折射星三者的几何关系如图3所示。

星光折射角α就通过视高度 ha反映了卫星和地球之间的几何关系，进而建立星光折射视高度 hg与折射角α、大气密度ρ之间的关系：

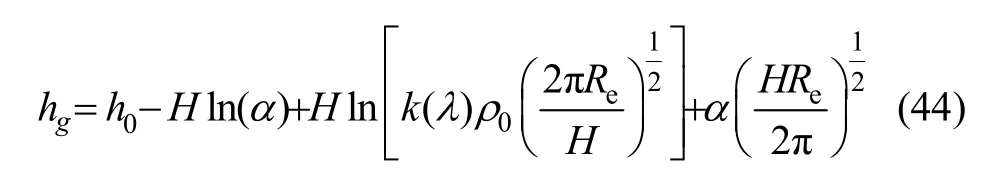
式中， k(λ)为散射参数， ρ0为高度 h0处的大气密度，H为密度标尺高度。

由图3中的几何关系，可得到：

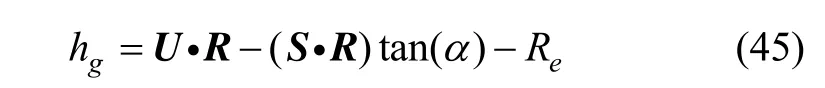
根据折射星在大气中的折射量就能确定当地地平方向，由式(44)和式(45)建立了折射测量与卫星位置之间的关系。

3.3.2 间接敏感地平观测方程

由图3给出的星光折射几何位置关系，定义矢量U为在恒星星光 Sz与卫星位置矢量 R组成的平面内垂直于恒星星光的单位矢量，即

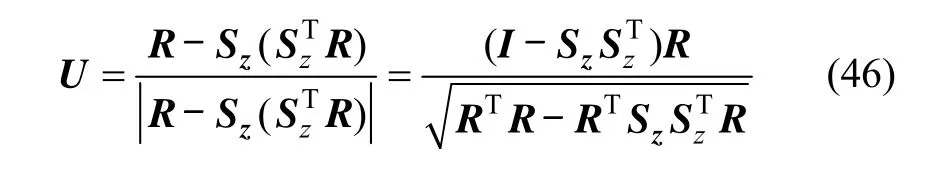
由图3所示，卫星位置R在矢量U方向上的投影表达式及其观测方程为：

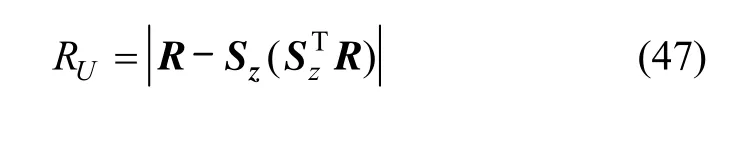
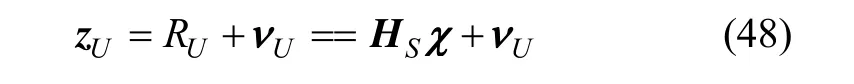
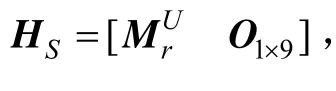
3.3.3 折射星预测

本文将折射星观测问题转换为星光折射观测参数的预测问题：当卫星沿某一轨道运行时，预先选定一组折射星，在卫星能观测到星光折射角α之前，提前确定对应的轨道位置和时刻以及恒星方向在当地轨道坐标系中的高度角和方位角能及时调整卫星姿态，使星敏感器视场在预定时刻对准指定折射星。

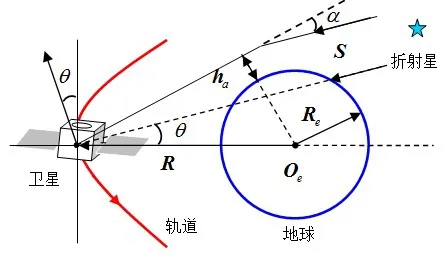
图4 水平高度角示意图Fig.4 The altitude angle figure

如图4 所示，恒星方向水平高度角可表示为：

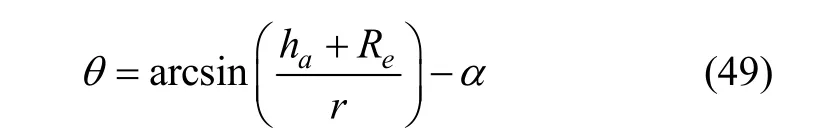
如果给定轨道参数半正焦弦P和偏心率e，卫星在轨道上的位置以真近点角f表示，则卫星至地心的距离为：

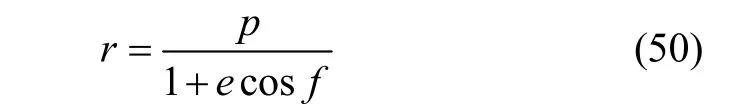
将式(50)带入式(49)，可得：

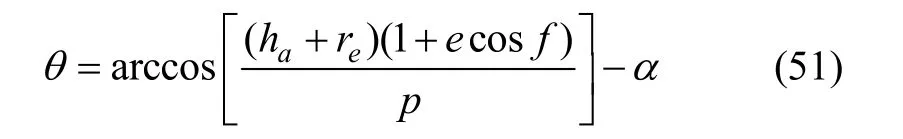
从卫星向地球方向看去，地球的投影在天球上是一个小圈。如图5所示，在卫星上进行观测，位于小圆圆周上的恒星星光都发生了折射，并且折射角都为α，恒星在小圆O上的位置由方位角φ给出。

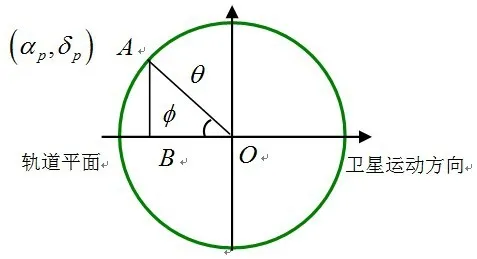
图5 恒星在轨道平面上方位表示Fig.5 The azimuth of star in orbit plane

如图5所示，设位于小圆O圆周上的折射星为A，设其轨道经度和纬度(即该折射星在地心轨道坐标系中的赤经和赤纬)分别为(αp,δp)。考虑图中的球面直角 三 角 形 OAB， 显 然OA= θ ， AB = δp，∠A OB = φ，OB = λ，由球面三角形关系，可得：

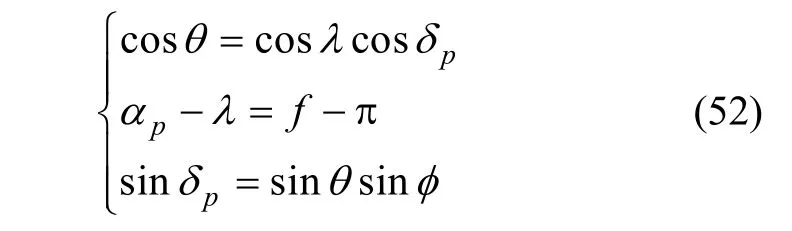
将式(51)和式(52)联立求解，则由(αp,δp)可确定星光折射观测点对应的真近点角 f，折射星方位角φ可由式(52)得到：

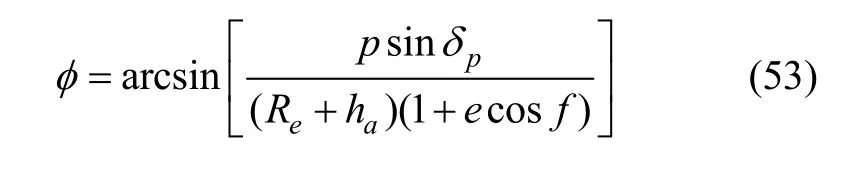
卫星标称轨道是由飞行任务确定的，轨道根数是已知的。星光折射的观测过程可由观测时刻卫星的真近点角f以及折射星的方向矢量在当地轨道坐标系中的方位角φ和高度角θ来描述，而高度角θ又可由卫星的真近点角确定，这样星光折射的观测过程可以由离散的二元数组(fi,θi)(i = 1,2,…, N)表示，N为在一个轨道周期内星敏感器所观测到发生折射的恒星数目。

在实际的星光折射观测过程中，对于(fi,θi)有一定的约束和要求。例如，要求 fi沿轨道的分布基本均匀，方位角 φi也有一定的范围规定： φmin≤φi≤φmax。方位角范围指出了恒星将擦射多少地平及地平的哪一个部分，一般选择：

由式(52)，可将(fi,θi) 的值转换为地心轨道坐标系和地心赤道惯性坐标系中的方位(αp,δp)、 (αi,δi)，这样对于(fi,θi)的约束条件可以转换为对于恒星方位的限制范围，应作为“开关 K”切换选取折射星时考虑的因素。对于给定的卫星标称轨道，恒星的轨道纬度 δp与其方向矢量的方位角φ有对应的关系，因此可以将对方位角 φi的约束条件转化为对 δp的约束条件：

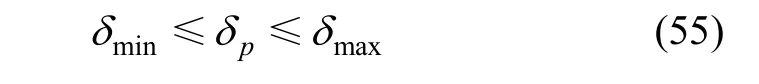
4 卫星自主定轨/定姿一体化系统

4.1 一体化系统原理

所设计一体化系统通过建立状态模型和观测模型，采用先进滤波算法，得到卫星轨道和姿态的最优状态估计。

4.2 滤波算法设计

根据设计的定位/定姿态原理，设计基于信息融合的自适应EKF算法具体步骤如下：

① 全局最优估计

经过分散化并行运算的滤波处理，得到的两个局部估计值 χ1(t)、χ2(t)和估计误差分别为 P1(t)、P2(t)，在主滤波器中按下式进行融合，得到全局估计值：

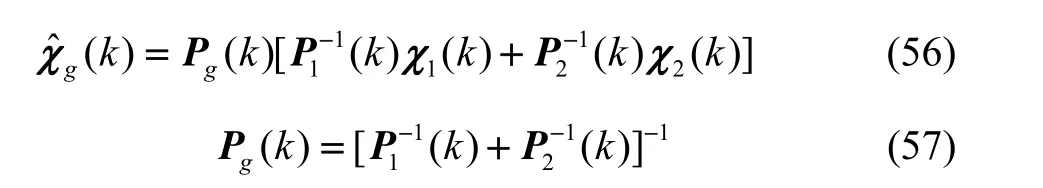
② 子滤波器估计与信息分配原则

将全局估计结果反馈给两个子滤波器，作为k时刻两个子滤波器估计值：

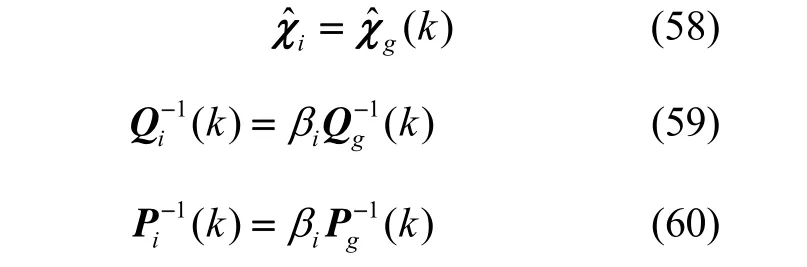
式中， i= 1,2， β1+ β2=1，0 ≤ βi≤1， Qg为系统状态噪声的方差阵。

信息分配因子选择的基本原则是在满足信息守恒公式的前提下与局部滤波器的滤波精度成正比，为了使组合导航系统具有更强的自适应能力和容错能力，使用基于估计误差阵P的范数的动态分配信息因子的算法。令

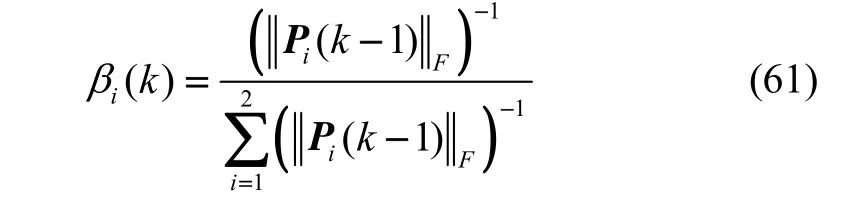
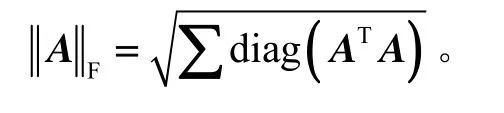
③ 信息融合观测更新

根据新的观测信息，对子滤波器1和子滤波器2进行EKF算法，具体算法步骤如下：

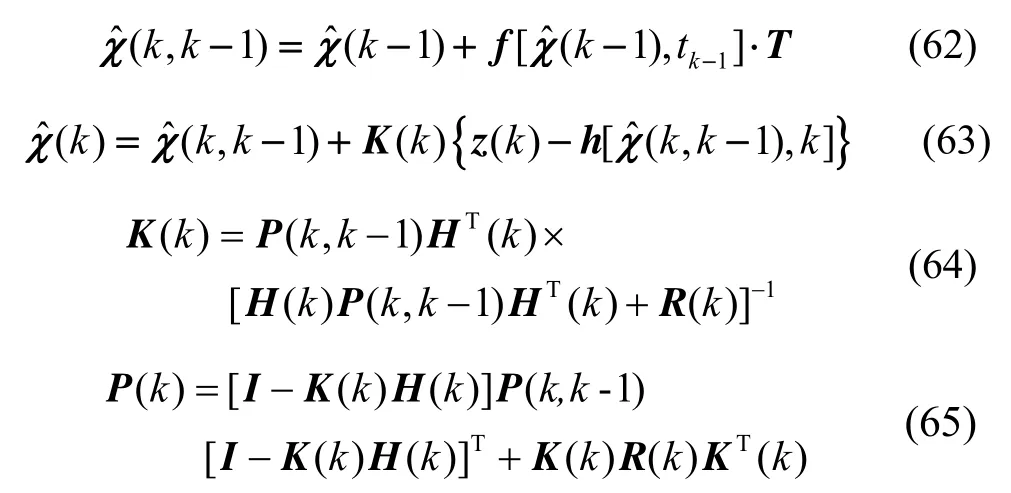
特别说明：1）当星敏感器2能观测到折射星导时，轨道滤波器进行观测更新和时间更新；2）当星敏感器2观测不到折射星时，轨道滤波器只进行时间更新。

5 计算机仿真及结果分析

5.1 仿真条件

为验证上述导航方法的有效性，在PC机上利用Matlab2012b软件进行数字仿真验证，仿真所使用卫星真实轨道数据由STK(Satellite Tool Kit)[15]软件产生，基本条件如下：

① 轨道参数：长半轴为6996.985 km，偏心率为0，轨道倾角为98.3087°，升交点赤经20°，近升角距102.8°，过近地点时刻0；

②姿态确定敏感器测量精度：星敏感器2"，三轴磁强计20 nT，测量噪声为高斯零均值白噪声；

③ 设星敏感器视场为20°×20°，能观测到4 m以上发生大气折射的恒星，这时在每个轨道周期内的折射观测在40次左右，但每次观测到折射星的数目不同。在此分析基础上，设每个轨道周期能观测到50颗折射星，大气密度模型精度1%，折射星由星光模拟程序根据卫星位置生成；

④ 设仿真时长：T=10 000 s，滤波周期：t=4 s；

⑤ 设卫星对地定向并且三轴姿态稳定，暂不考虑卫星轨道/姿态机动。

5.2 数值仿真

为验证本文的算法，对所设计组合导航模式进行计算机仿真。① 自主定位

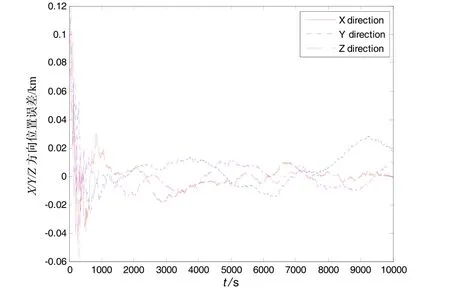
图7 X/Y/Z方向位置误差Fig.7 Position error in X/Y/Z direction

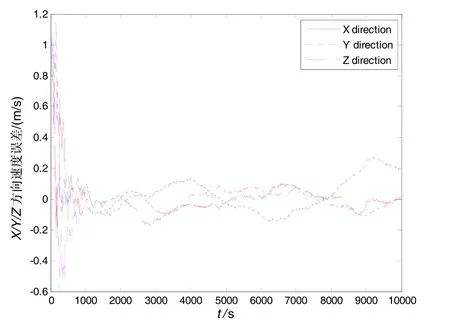
图8 X/Y/Z方向速度误差Fig.8 Velocity error in X/Y/Z direction

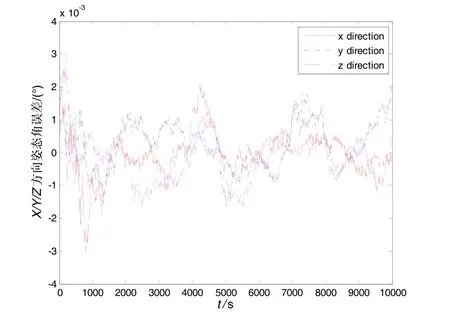
图9 X/Y/Z方向姿态角误差Fig.9 Attitude angle error in X/Y/Z direction

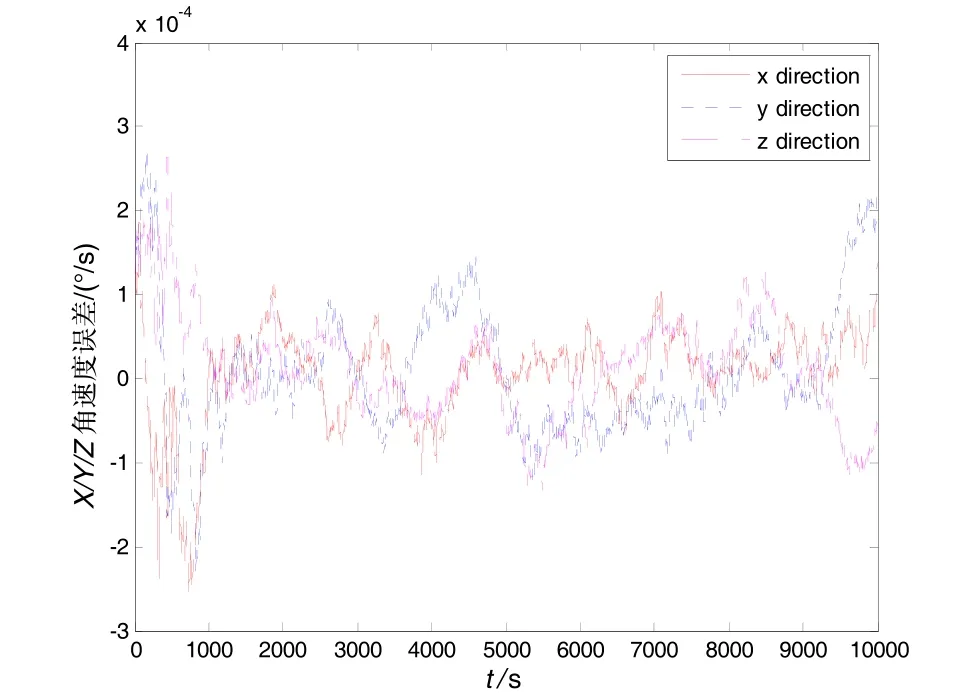
图10 X/Y/Z方向姿态角速度误差Fig.10 Attitude angle velocity error in X/Y/Z direction

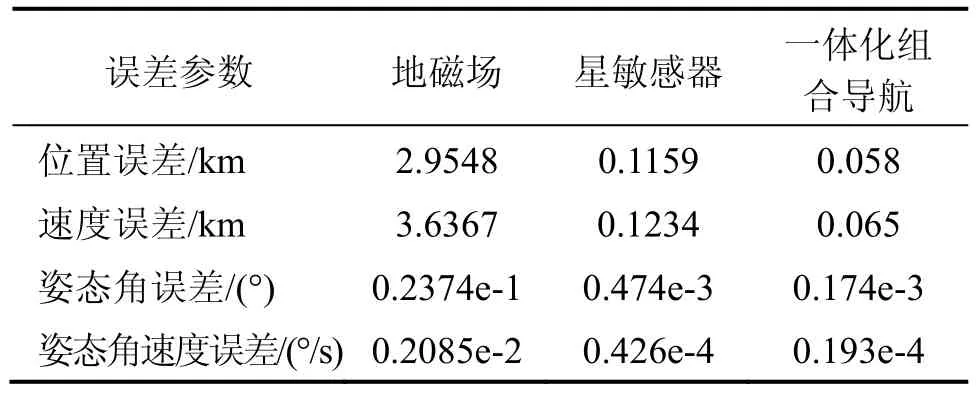
表1 不同导航算法滤波结果比较Tab.1 Comparison on filter results of different algorithms

5.3 结果分析

对图7～图10及表1给出的三种导航方法数值仿真结果进行分析，可得以下结论：

① 利用地磁场信息同时进行定轨和定姿，由于卫星轨道动力学 J2模型和姿态动力学模型精度有限，以及三轴磁强计测量精度较低，因此轨道和姿态信息精度较低，仅适用中低精度卫星自主导航；

② 星敏感器能够提供高精度的姿态信息，同时利用星敏感器间接敏感地平导航精度较高，但是由于折射星数量以及观测条件有限，不能连续进行长时间连续导航。

③ 所设计地磁场/天文的一体化组合导航系统不仅克服了地磁场精度不高和天文导航不连续的情况，而且充分利用了敏感器信息互补增强系统对不同情况的适应能力，取得很好的导航效果，适用于中高精度卫星同时定轨和定姿。

6 小 结

本文利用三轴磁强计和星敏感器作为观测敏感器建立了轨道和姿态动力学方程，推导了基于信息融合的卫星轨道姿态一体化确定算法，并进行了数学仿真，结果表明了该算法的可行性和有效性，仿真精度表明能够满足高中精度小卫星轨道和姿态确定任务需求。通过本文研究探索了一条实现卫星轨道和姿态同时确定的新途径和新方法，改善了系统的确定精度，提高了星上常用敏感器的利用效率，为“好、快、省”的微小卫星设计与研制提供了一条可行的技术途径。

（References）：

[1] Lemay J L. High altitude navigation study[R]. The Aerospace Corporation. EI Segundo, California. Report TR0073 (3491)-1, June 29, 1973.

[2] 周军，葛致磊，施桂国，等. 地磁导航发展与关键技术[J]. 宇航学报，2008，29(5)：1467-1472

ZHOU Jun, GE Zhi-lei, SHI Gui-guo, et al. Key technique and development for geomagnetic navigation[J]. Journal of Astronautics, 2008, 29(5): 1467-1472.

[3] 房建成，宁晓琳. 航天器自主天文导航原理与方法[M].北京：国防工业出版社，2006：1-15.

[4] 房建成，宁晓琳. 深空探测器自主天文导航方法[M].北京：国防工业出版社，2006：1-15.

[5] Gusarov A. Levron D, Paperno E, Shuker R, Baranga A B. Three-dimensional magnetic field measurements in a single SERF atomic magnetometer cell[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4778-4481.

[6] Deutschmann J, Bar-Itzhck I Y. Evaluation of attitude and orbit estimation using actual earth magnetic field data[J]. Journal of Guidance, Control and Dynamics, 2001, 24(3): 616-626.

[7] Hee J, Psiaki M L. Tests of magnetometer / sun-sensor orbit determination using flight data[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Montreal, CA, 2001: 1-14.

[8] Psiaki M L. Autonomous low-earth orbit determination from magnetometer and sun sensor data[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(2): 296-304.

[9] Deutschmann J, Bar-Itzhck, I Y. An innovative method for low cost, autonomous navigation for low earth orbit satellite[C]//Proc. of the 1998 AIAA/AAS Astrodynamics Specialist Conf.. Boston, Massachusetts, 1998.

[10] Gebre-Egziabher D, Elkaim G, Powell J, Parkinson B. Calibration of strapdown magnetometers in magnetic field domain[J]. ASCE Journal of Aerospace Engineering, 2006, 19(2): 1-16.

[11] Wang Peng, Zhang Yingchun. Research on a method of autonomous navigation based on magnetometer and sun sensor[J]. Systems Engineering and Electronics, 2013, 35 (1): 132-137.

[12] Zhao M H, Shi M, Zeng Y L, et al. Satellite autonomous orbit determination using magnetometers[J]. Systems Engineering and Electronics, 2004, 26(9): 1236-1238.

[13] Gao C S, Jing W X, Zhang Y. Autonomous navigation of low-earth-orbit satellites using magnetic measurements by unscented kalman filter[J]. Chinese Space and Technology, 2006, 23(2): 27-32.

[14] Wang S Y, Yang X, Cheng Y. Algorithm for autonomous navigation of low earth orbit satellite using magnetic measurement[J]. Journal of Astronautics, 2003, 24(6): 634-637.

[15] 杨颖，王琦. STK在计算机仿真中的应用[M]. 北京：国防工业出版社，2005.

[16] Guo Caifa, Li Anliang, Cai Hong. Algorithm for geomagnetic navigation and its validity evaluation[C]//2011 IEEE International Conference on Computer Science and Automation Engineering. Shanghai, China, 2011, Vol.1: 573-577.

一种小卫星高精度自主定轨/定姿一体化新方法

王 鹏1,2，张迎春3

New method for high-precision autonomous determination of integrated orbit/attitude of small satellite

WANG Peng1,2, ZHANG Ying-chun3
(1. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 2. Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology of Ministry of Education, Southeast University, Nanjing 210096, China; 3. Harbin institute of technology, Institute of Astronautics, Harbin 150001, China)

A new method for simultaneously determining the orbit and attitude of satellite based on threeaxis-magnetometer (TAM) and celestial data is presented, which is a breakthrough over traditional pattern of separately treating the satellite’s orbit and attitude. Firstly, the system state equation is established by analyzing the satellite orbit dynamics J2model and deducing the satellite attitude dynamics model. By utilizing the differences between the measured and computed magnetic field components, a set of measurement equation is established. By utilizing the attitude information and indirect sensing horizon from star sensor, another group of measurement equations are established. The autonomous navigation method and algorithm are designed and simulated. The results of computer simulation show that the proposed system improves the navigation precision and reliability.

three-axis magnetometer; celestial navigation; integrated orbit and attitude determination; information fusion

联 系 人：张迎春（1961—），男，教授、博导，研究方向为飞行器设计。

1005-6734(2014)06-0741-07

10.13695/j.cnki.12-1222/o3.2014.06.008

V448.2

A

2014-07-01；

2014-10-20

江苏省自然科学基金（BK20130636）；中国航天科技集团公司卫星应用研究院创新基金项目（2012-1510）；东南大学微惯性仪表与先进导航技术教育部重点实验室开放基金项目（201211）

王鹏（1979—），男，博士，讲师，研究方向航天器组合导航及姿态确定技术。E-mail：snowpeng@gmail.com