一种航天飞行器的INS/CNS自主导航方案

（1. 北京航空航天大学，仪器科学与光电工程学院，北京 100191；2. 中国舰船研究院，北京 100192；3. 中广核工程有限公司，深圳 518040；4. 二炮装备研究院，北京 100085）

（1. 北京航空航天大学，仪器科学与光电工程学院，北京 100191；2. 中国舰船研究院，北京 100192；3. 中广核工程有限公司，深圳 518040；4. 二炮装备研究院，北京 100085）

传统的天文导航方法由于受水平基准精度的制约，难以进一步提高定位精度。针对INS/CNS组合导航方法对水平基准依赖的问题，提出了一种新颖的基于星光折射技术的INS/CNS自主组合导航方案。将惯性系下的非线性惯导误差传播方程作为系统状态方程，将星敏感器测得姿态和星光折射信息作为量测，采用UKF滤波算法，构成全面最优的INS/CNS组合导航。仿真结果表明，星敏感器精度为3″时，导航系统的定位精度优于200 m，姿态精度优于3″，导航定位精度随所使用的折射星数目增多明显提高，且方案在系统大角度误差条件下仍然适用。

星光折射；自主导航；非线性；UKF

传统的天文导航是基于“高度差法”的，观测点的位置和方位信息包含在天体的地平坐标（高度角和方位角）中[1]。INS/ CNS组合导航一般利用地平仪、空间六分仪直接敏感地平或利用惯导系统输出的水平姿态信息获得天体的地平坐标作为观测量[2-5]，再结合飞行器的运动方程和滤波方法估计出载体的位置信息。目前国内外惯导平台的水平精度的最高水平为4″～8″，一般为20″～40″，天文导航的定位精度只能达到海里级；地平仪(如红外地平仪)的精度目前只能达到0.02°，最终定位精度约为1～3 km；利用空间六分仪，天文导航可以得到较高的定位精度，但是该设备过于复杂且成本过高，不利于大范围使用。可见水平基准精度已成为INS/ CNS组合导航精度向高精度方向发展的瓶颈。

利用星光折射间接测量地平法是20世纪80年代初发展起来的一种低成本、高精度的自主卫星导航方法。它仅利用星敏感器来量测折射角，结合大气层的较精确的数学模型来间接敏感地平，从而实现载体的精确定位。星光折射自主导航方法一种摆脱水平基准精度制约、提高自主定位精度的有效方法。我国一些研究所和高校都对这种导航技术进行了深入研究，并取得了一些研究成果[6-10]，目前已有的研究都是针对基于轨道运动学模型的空间轨道飞行器，如卫星、导弹的自主定轨、定位问题。

随着大视场星体快速检测技术发展，能够完成某一时刻的多星同步检测，确定载体相对惯性系的姿态，可以通过最优估计的方法估计补偿惯导系统中因陀螺漂移引起的误差，然而这种模式对加速度计等其他因素引起的误差补偿效果不明显，它不是全面最优的。

本文利用惯性系下基于加性四元数的非线性惯导误差传播方程作为组合导航系统的状态方程，将基于星光折射技术的天文导航推广到非轨道运动的航天飞行器，同时利用星敏感器得到的相对于惯性空间的高精度姿态信息，采用无迹卡尔曼滤波器（Unscented Kalman filter, UKF）[11]进行信息融合，构成非线性的INS/ CNS组合导航系统，对系统状态进行全参量最优估计，实现全面自主导航。星敏感器间接敏感的地平信息和载体姿态都是惯性系下的信息，便于进行误差分析，并且省去了转换到当地地理水平坐标系过程中产生的转换误差，降低了系统的计算量。该INS/ CNS组合导航方案高效地利用了星敏感器的高精度量测信息，系统成本低、导航精度高、自主性强，具有较高的实际应用价值。

1 星光折射导航定位原理

星光通过地球大气时，光线会向地心方向偏折。航天器上观测的折射光线相对于地球的视高度为 ha（星光切向高度），当星敏感器观测到一个折射角θ时，根据大气模型，可计算出星光视高度 ha[6]。

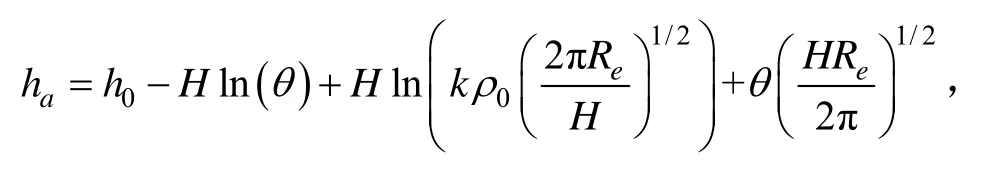
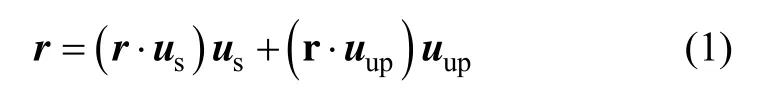
引入一个恒星 LOS的真空切向高度 hv（在没有大气层的情况下恒星LOS的切向高度）。真空切向高度 hv在卫星位置和折射角之间起到了了纽带作用。从图1可以看出 hv和星光矢量、卫星位置的关系如下，并且与星光折射的影响无关：

同时，从图1我们也可以得到 hv与θ、ha的关系：

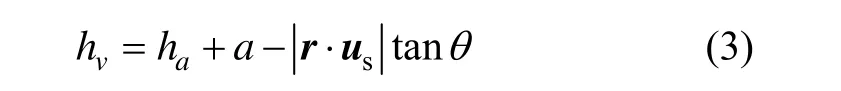
式(3)表明了星光折射量测是如何与卫星位置解算联系起来的。将(3)代入(2)，忽略小量a，并假设θ = tan θ，得到：

将(4)代入(1)可得卫星位置与折射角之间的关系：

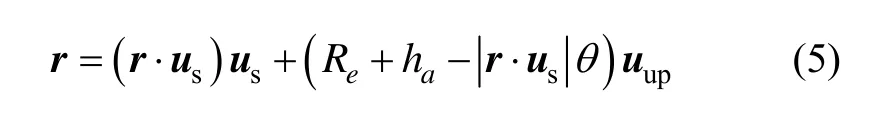
2 INS/ CNS组合导航系统模型

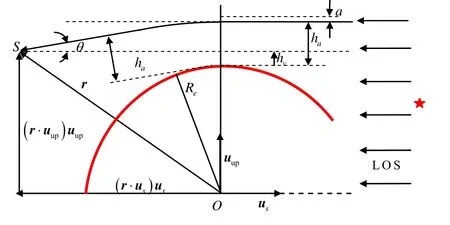
图1 星光折射几何示意图Fig.1 Stellar refraction geometry.

在惯性空间内，恒星的方位基本保持不变，尽管星敏感器的像差、地球极轴的进动和章动以及视差等因素使得恒星方向有微小的变化，但它们造成的姿态误差小于1″。因此星敏感器相当于没有漂移的陀螺，因此用天文量测信息修正惯性器件误差是可行的[3]。星光折射方法利用高精度的星敏感器量测星光折射角，星光折射角与大气密度之间存在较精确的函数关系，而大气密度随高度变化也有较准确的模型，从而可以精确的确定出折射星光在大气层中的高度，这个量测量反映了飞行器与地球之间的几何关系，从中可以获得间接的地平信息，解算出载体在地心惯性坐标系中的位置矢量。因此，利用星敏感器敏感多颗恒星，可以确定载体在惯性系下的姿态和位置，结合惯性系下惯导误差传播方程和先进的滤波方法，可以对导航参数进行估计校正，提高精度。

本文将姿态信息与星光折射敏感地平信息作为观测信息，充分利用星敏感器的量测信息，与惯导系统构成非线性的INS/CNS组合导航系统，利用UKF实现全面最优的组合导航，为飞行器提供高精度的导航信息。

2.1 状态方程

星敏感器得到的姿态和星光折射法敏感地平都是相对于惯性空间的信息，本文采用J2000地心惯性系i作为导航坐标系不会产生转换到当地地理水平坐标系的转换误差并且便于误差分析。

在捷联惯导系统中，四元数通常用来表示坐标系间的转换关系，同样可以用四元数描述导航系统的平台失准角。本文推导了惯性系下基于加性四元数的非线性捷联惯导误差传播方程。

用加性四元数误差定义计算四元数与真实四元数的差[12]：

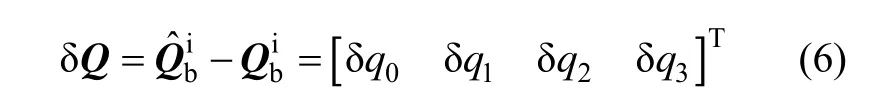
惯性系i下捷联惯导系统的导航方程表示为：

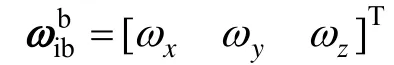
由式(7)得，系统的速度微分方程为：

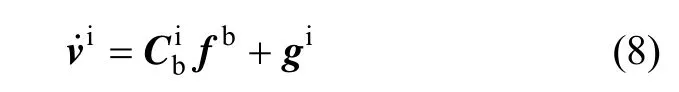
设速度误差、加速度计量测误差、姿态矩阵计算误差以及地球引力加速度计算误差分别为、、、。存在误差时式(6)中的速度微分方程变为：

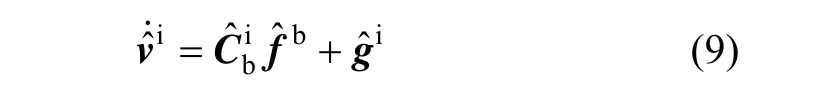
式(8)可以表示为：

式(9)与式(10)相减得：

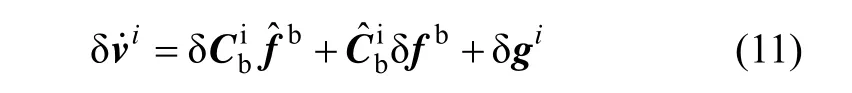
空天飞行器的覆盖范围广，飞行时间长，影响导航的最大摄动因素是由地球椭球模型引起的重力加速度偏差，因此考虑地球引力加速度误差带来的影响。

不考虑地球非球形引力时推导结果如下：

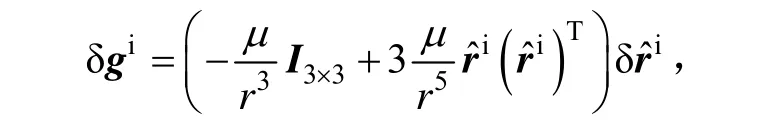
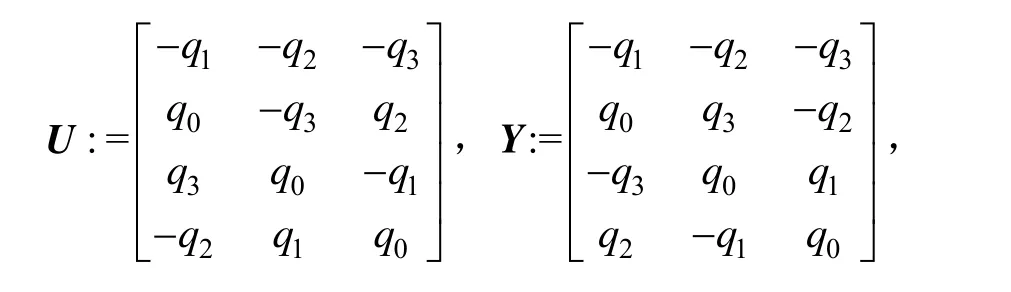
满足：

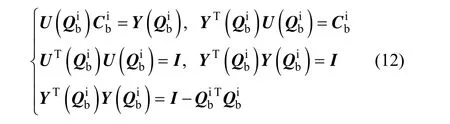
由式(12)可得姿态矩阵的计算误差：

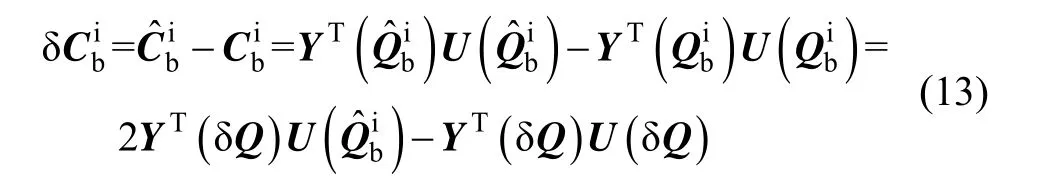
由文献[7]有等式：

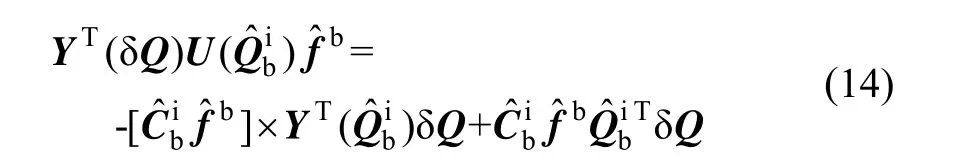
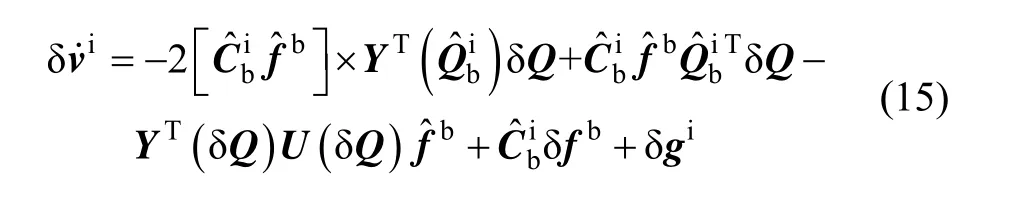
系统的姿态微分方程为：

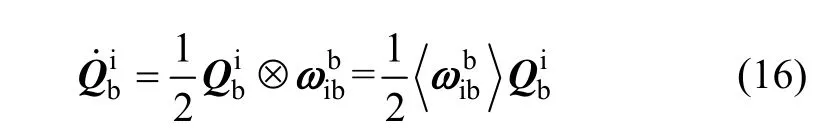
捷联惯导系统姿态四元数更新微分方程为：

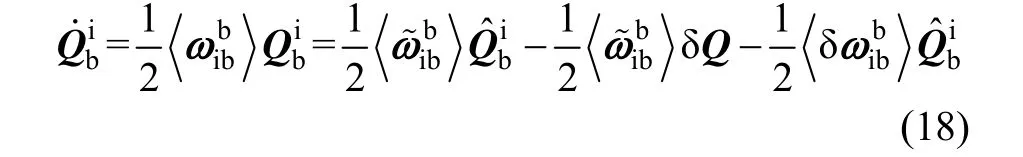
根据四元数特性可知：

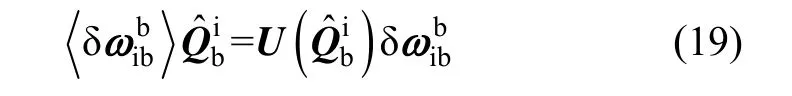
式(17)减去式(18)得姿态误差方程：

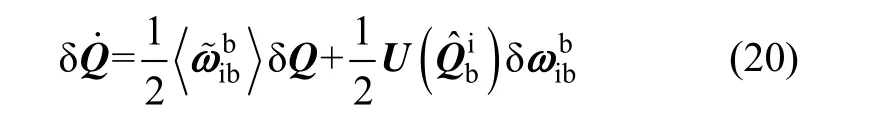
式(20)为线性微分方程，且在推导过程中没有小量假设，因此该方程在大机动、大失准角的情况下仍能够准确描述惯导系统的误差传播特性。

位置误差只和速度误差有关，表示为：

陀螺仪误差和加速度计误差在本文中作为随机常值来考虑。系统状态量为：位置误差、速度误差、姿态四元数误差、陀螺误差、加速度计误差，可以建立INS/ CNS组合导航系统的状态方程：

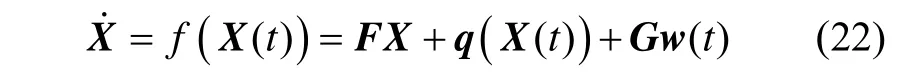
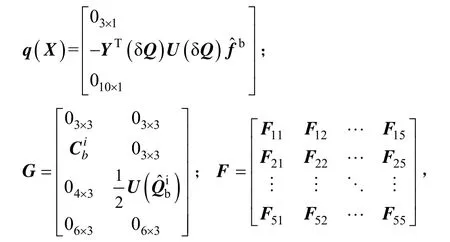
非零元素为：

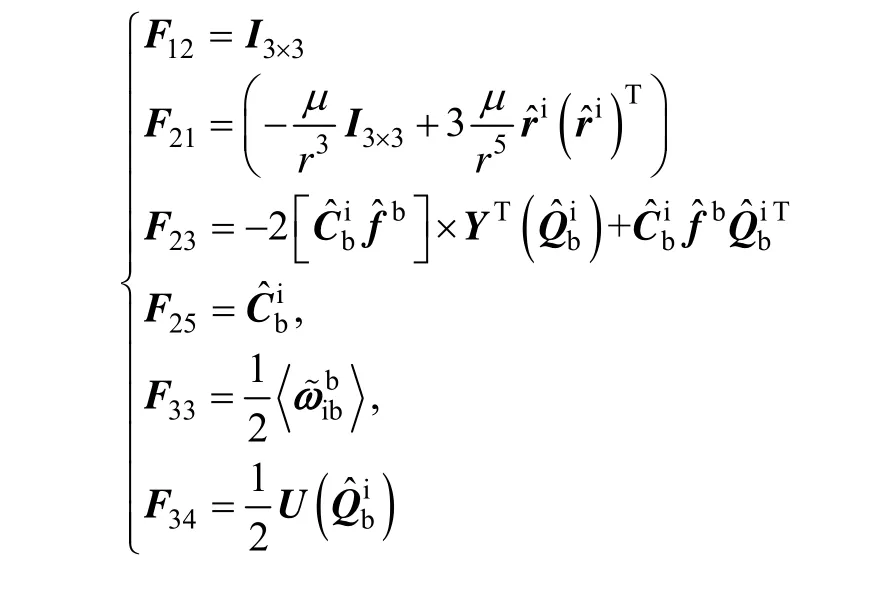
2.2 量测方程

2.2.1 星敏感器姿态量测方程

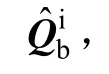
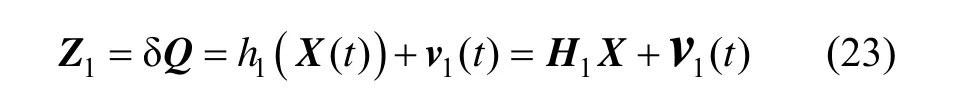
2.2.2 星光折射间接敏感地平的量测方程

以位置矢量在垂直方向的投影 r·uup作为观测量。这将有利于综合考虑星敏感器精度及大气折射模型的不确定性对导航精度的影响。

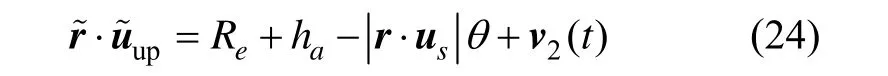
式中，v2为量测噪声，视为均方差为 R2的高斯白噪声。

星光折射的量测误差主要由星敏的器件误差和大气模型的不确定性造成。对式(4)两边进行微分，可得星光折射量测误差与星光折射角误差dθ和大气模型误差 dρ0之间的关系：

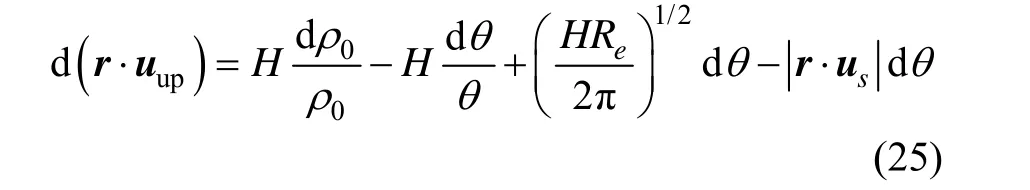
星光折射角随着切向高度的降低而增大，切向高度越低越有利于的星光折射角的观测。但是，由于对流层大气不稳定，无法建立准确的大气模型，不适于星光折射间接敏感地平。而同温层的大气密度模型比较稳定，变化主要取决于纬度和季节。通过气象火箭和气球对高度在25 km处的平流层的观测结果表明，热带地区大气密度的不确定性在 1%以内，在夏季半球从赤道变化到极点时大气密度的变化会增加2倍至3倍。

由美国标准大气可知，在ha= 25 km处，H=6.366 km，ρ0=40.084 gm/m3，θ = 148.1′′。从式(32)中的第一项可得1%的大气密度误差会导致63.7m的星光折射量测误差；第二、三、四项是与星光折射角误差相关的误差项，量测精度为 3″的星敏感器会导致高度 40 km处飞行器的星光折射量测误差为138.5 m。星光折射角误差dθ和大气模型误差 dρ0共同引起的量测误差为152.4 m。

星光折射的量测方程为：

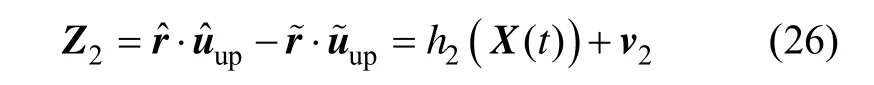
将星敏姿态量测与星光折射量测合并得到组合导航系统的量测信息：

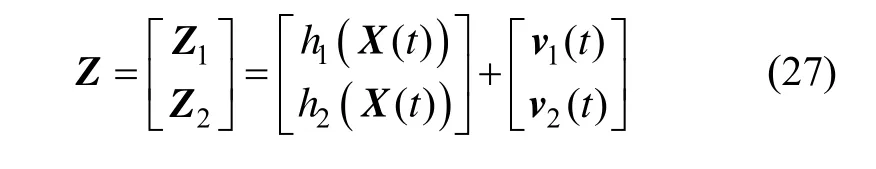
3 数值仿真与分析

为验证本文提出的方法的有效性，利用MATLAB对算法进行数值仿真，并将EKF和UKF滤波器的组合导航结果进行了比较。仿真条件设置如下：

① 总飞行时间为2 h。三轴初始位置误差为1 km，初始速度误差为3 m/s，初始姿态误差为0.5°。

② 陀螺常值漂移0.1 (°)/h、随机漂移为0.01 (°)/h，加速度计的常值偏置为100 μg、随机偏置为10 μg。

③ 星敏感器的量测精度为 3″，则姿态量测误差为3″，星光折射量测误差160 m。

④ 惯导系统采样周期0.01 s，天文导航系统姿态量测输出周期为1 s、星光折射量测输出周期为5 s，组合导航滤波状态更新周期为1 s，信息融合周期为5 s。

图2～图4可以看出，利用星敏感器星光折射量测和姿态量测与惯导系统组合导航时，EKF得到三轴位置精度分别为148.9 m、244.7 m、232.4 m，速度精度分别为0.25 m/s、0.25 m/s、0.24 m/s，姿态精度分别为6.1″、18.7″和8.2″。UKF滤波收敛速度较快，且滤波稳定后三轴位置和速度的估计精度高于EKF算法，分别为90.8 m、136.6 m、148.0 m，速度精度分别为0.26 m/s、0.37 m/s、0.62 m/s。由于UKF采用加性四元数进行非线性误差建模姿态精度几乎没有损失，组合导航姿态精度达到3″以内，与星敏感器的量测精度相当，俯仰、横滚和航向姿态角精度分别为2.27″、2.21″和2.17″。

图2 UKF与EKF组合导航位置误差比较Fig.2 Position errors comparison with UKF and EKF

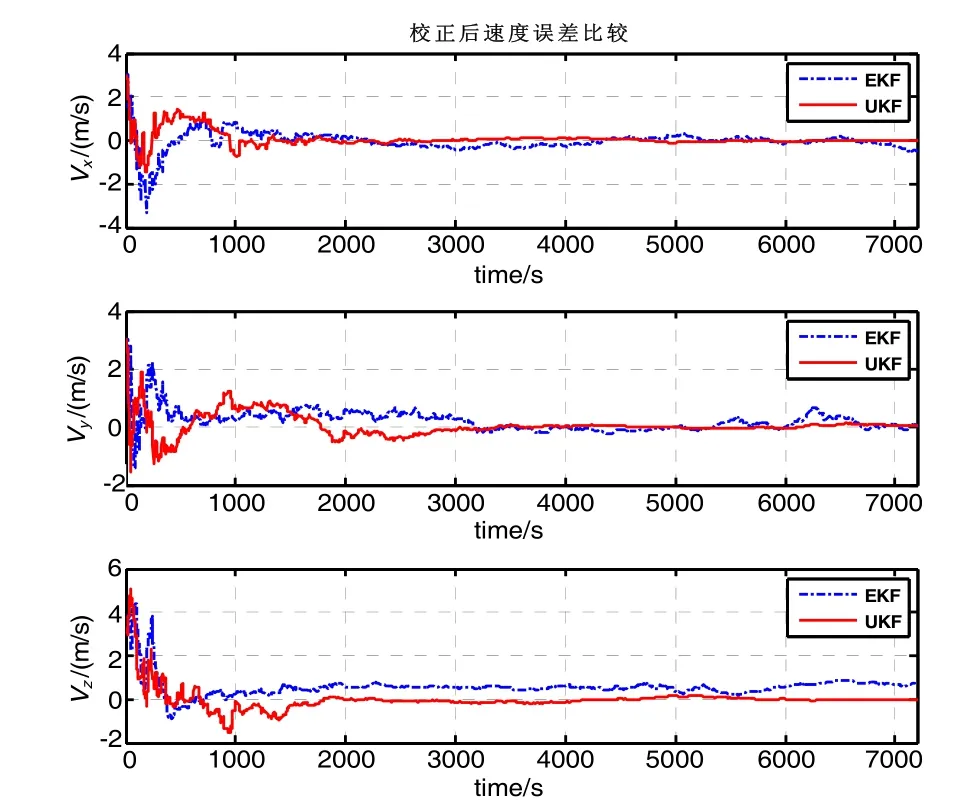
图3 UKF与EKF组合导航速度误差比较Fig.3 Velocity errors comparison with UKF and EKF.

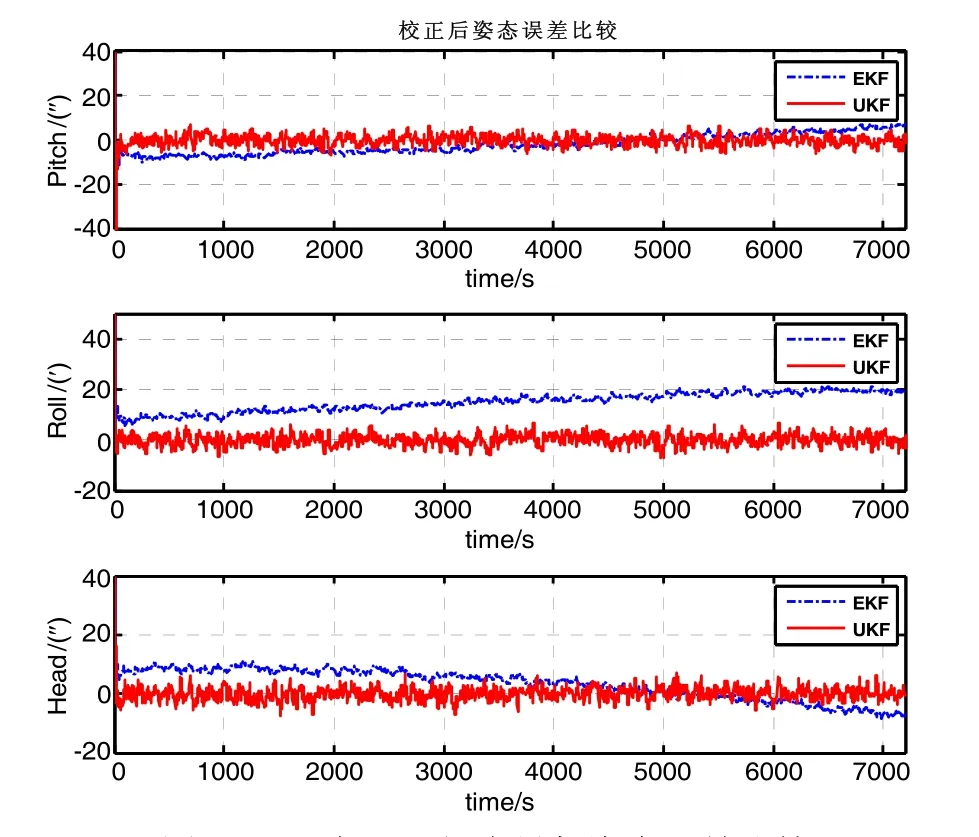
图4 UKF与EKF组合导航姿态误差比较Fig.4 Attitude errors comparison with UKF and EKF.

图5 大角度误差组合导航姿态误差Fig.5 Position errors with large angular misalignment

为了验证系统存在大角度误差时导航方案的有效性，设初始姿态误差为10°，并将采用EKF和UKF的组合导航结果进行了比较，仿真结果如图 5、图 6所示。从图5可以看出，与EKF算法相比，UKF算法的收敛速度快，且位置精度达到190 m。图6中，UKF估计的姿态误差迅速收敛，精度优于3″，而采用EKF算法得到的姿态误差是发散的。

图6 大角度误差组合导航姿态误差Fig.6 Attitude errors with large angular misalignment.

另经仿真验证，SIN/ CNS组合导航系统的定位精度随观测折射数量的增多得到明显提高，见表1。

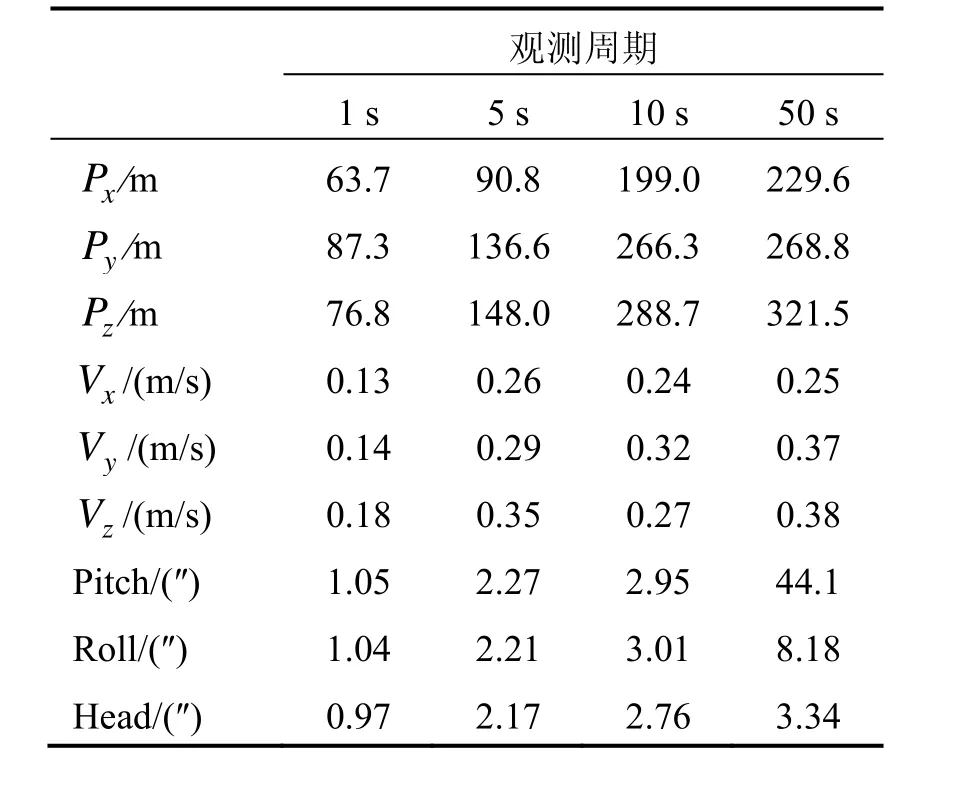
表1 观测折射星数量与导航精度的关系Tab.1 Impact of number of visible refracted stars on navigation accuracy.

4 结 论

本文提出一种基于星光折射间接敏感地平和星敏测姿信息的INS/ CNS组合导航方案，高效地利用了星敏感器的高精度量测信息，且摆脱了传统INS/ CNS组合导航方法对水平基准的依赖，提供高精度的全参数的导航信息。由于采用了基于加性四元数的非线性误差模型，算法在系统存在大角度误差的情况仍然适用。另经验证，导航精度随观测折射数量的增多得到明显提高。该导航方案具有成本低、导航精度高、自主性强的特点，不仅能用于地球轨道卫星导航，还能为空天飞行器、高空长航时飞行器等提供导航服务，具有较高的实际应用价值。

另外，星光折射定位方法受大气模型精度的影响较大，因此分析引起大气模型误差的因素，并对这些误差进行补充，建立准确的观测模型是该方法能发用于实际的关键，需进一步深入研究。

（

）

[1] He J. Survey of overseas celestial navigation technology development[J]. Ship Science and Technology, 2005, 27(5): 91-96.

何炬. 国外天文导航技术发展综述[J]. 舰船科学技术，2005，27(5)：91-96.

[2] Xiong Z, Liu J Y, Yu F. Research of airborne INS/CNS integrated filtering algorithm based on celestial angle observation[J]. Journal of Astronautics, 2010, 31(2): 397-403.

熊智，刘建业，郁丰，陈海明. 基于天文角度观测的机载惯性/天文组合滤波算法研究[J]. 宇航学报，2010，31(2)：397-403.

[3] Wu X, and Wang X L. A SINS/ CNS deep integrated navigation method based on mathematical horizon reference[J]. Aircraft Engineering and Aerospace Technology, 2011, 83(1): 26-34.

[4] Yang S J, Yang G L, Shan Y D, et al. SINS/CNS tightly integrated navigation algorithm for aerospace vehicles[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 478-483.

[5] Xiong J, Wei L S, Guo H etc. SINS/CNS nonlinear tightly integrated method based on additive quaternion[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 596-600.

熊剑, 魏林生, 郭杭等. 基于加性四元数的SINS/ CNS非线性紧组合方法[J]. 惯性技术学报，2012，20(5)：596-600.

[6] Qian H M, Sun L, Cai, J N, Huang W. A starlight refraction scheme with single star sensor used in autonomous satellite navigation system[J]. Acta Astronautica, 2014, 96: 45-52.

[7] Ning X L, Wang L, Bai X, Fang J C. Autonomous satellite navigation using starlight refraction angle measurements[J]. Advances in Space Research, 2013, 51(9): 1761-1772.

[8] Ning X L, Wang L, Bai X, Fang J C. A scheme design of satellite autonomous navigation system based on stellar refraction[J]. Journal of Astronautics, 2012, 30(11): 1601-1610.

宁晓琳，王龙华，白鑫贝，房建成. 一种星光折射卫星自主导航系统方案设计[J]. 宇航学报，2012，30(11)：1601-1610.

[9] Wang X L, Ma S. A celestial analytic positioning method by stellar horizon atmospheric refraction[J]. Chinese Journal of Aeronautics, 2009, 22(3): 293-300.

[10] Qian H, Sun L, Cai J and Peng Y. A novel navigation method used in a ballistic missile [J]. Measurement Science and Technology, 2013, 24(10): 105011.

[11] Hu H D and Huang X L. SINS/CNS/GPS integrated navigation algorithm based on UKF[J]. Journal of Systems Engineering and Electronics, 2010, 21(1): 102-109.

[12] YU MJ, LEE J G, PARK H W. Comparison of SDINS in-flight alignment using equivalent error models [J]. IEEE Transaction on Aerospace and Electronic System, 1999, 35(3): 1046-1054.

一种航天飞行器的INS/CNS自主导航方案

杨淑洁1，杨功流1，尹洪亮2，邹成伟3，李 霄4

Scheme design of autonomous integrated INS/CNS navigation systems for spacecraft

YANG Shu-jie1, YANG Gong-liu1, YIN Hong-liang2, ZOU Cheng-wei3, LI Xiao4
(1. School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China; 2. China Ship Research and Development Academy, Beijing 100192, China; 3. China Guangdong Nuclear Power Engineering Co., Ltd., Shenzhen 518040, China; 4. Second Artillery Equipment Research Academy, Beijing 100085, China)

The navigation accuracy of traditional INS/CNS is difficult to improve due to limited accuracy of horizontal reference. In view of this problem, a novel scheme design of autonomous INS/CNS integrated navigation systems was proposed based on the stellar refraction technology. The nonlinear error equation of INS in inertial frame was derived, and it was chosen as the error state dynamic equation of the INS/ CNS integrated system. The measurement was the stellar refraction angle and the attitude information of the star sensors. UKF was utilized to obtain all-state optimal estimation. Simulation results show that the precision of positioning provided by UKF is better than 200 m, the precision of attitude determination is better than 3″, and the system’s navigation performance can be significantly improved

stellar refraction; autonomous navigation; nonlinearity; UKF

联 系 人：杨功流（1967—），男，教授，博士生导师。E-mail：bhu17-yang@139.com

1005-6734(2014)06-0728-06

10.13695/j.cnki.12-1222/o3.2014.06.006

V488.2

A

2014-07-16；

2014-10-15

中央高校基本科研业务费专项资金资助项目（YWF-10-01-B30）

杨淑洁（1986—），女，博士研究生，从事惯性技术、天文导航。E-mail：shujiehit@163.com