捷联惯导晃动基座四元数估计对准算法
2014-10-21海军工程大学电气工程学院武汉430033天津航海仪器研究所天津300131
(1. 海军工程大学 电气工程学院,武汉 430033;2. 天津航海仪器研究所,天津 300131)
(1. 海军工程大学 电气工程学院,武汉 430033;2. 天津航海仪器研究所,天津 300131)
针对捷联惯导晃动基座下的初始对准问题,提出了一种基于四元数估计(QUEST)的抗干扰对准算法。将惯性系对准方法中,求取初始姿态阵的问题转化为基于观测矢量确定载体姿态的Wahba问题,利用四元数估计算法得到最小二乘意义下载体初始姿态的最优四元数解。阐述了四元数估计算法的基本原理,详细给出了基于四元数估计算法的捷联惯导晃动基座对准方案。进行了车载实验,实验结果表明:四元数估计对准算法姿态角误差的收敛速度优于双矢量定姿对准算法,同时可进一步提高对准精度。经120 s对准后,水平姿态误差在5″以内,航向误差在1.3′以内。
捷联惯导;晃动基座;初始对准;Wahba问题;四元数估计算法
捷联惯导的初始对准可分为粗对准和精对准两个阶段[1]。目前,捷联惯导晃动基座粗对准方案大都采用惯性系方法解决,该方法将传统解析式对准中载体角晃动干扰转化为线晃动干扰,可有效解决摇摆基座下捷联惯导快速粗对准的问题[2]。惯性系对准法[3]将载体姿态阵分解为三部分,以初始地理系和载体系凝固而成的惯性系作为过渡,运用双矢量定姿原理中的TRAID算法[4]计算初始姿态阵。TRAID算法中的两个矢量具有不对称性,Bar-itzhack由此证明了由TRAID算法得到的姿态阵解不是最优的,并提出了一种最优TRAID 算法(Optimized TRAID)[5]。文献[6]基于Optimized TRAID算法,提出了基于最优三轴姿态测定算法的捷联惯导粗对准方法。该算法分别以不同的观测矢量作为基准,进行两次姿态阵运算,并根据两个观测矢量的统计特性对两个姿态阵进行加权处理,对准精度优于传统的 TRAID算法。上述基于双矢量定姿原理的粗对准算法均过于简单,只采用了对准期间两个时刻的加速度计信息,而其余大部分观测信息并未充分利用,所选时刻观测矢量的测量精度对最终的对准结果影响较大。Wahba将利用观测矢量确定姿态的问题描述为最小二乘意义下求解最优正交姿态阵的问题[7],Shuster提出的四元数估计算法(QUEST)[8]给出了Wahba问题的最优四元数估计值。
本文受到文献[7]的启发,提出了基于四元数估计算法的捷联惯导晃动基座对准方法。该算法可充分利用每一时刻的加速度计信息,与基于双矢量定姿算法的对准方法相比,可进一步提高对准精度。
1 对准方案
1.1 坐标系说明
b(t)系:t时刻的载体系,方向为右前上。
n(t)系:t时刻的导航系,采用东北天地理坐标系。
ib(0)系:由0时刻的载体系凝固而成的惯性坐标系。
in(0)系:由0时刻的导航系凝固而成的惯性坐标系。
1.2 对准基本原理

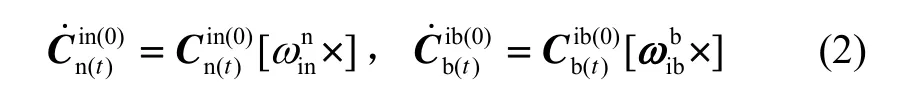
晃动基座下载体的线速度 vn和线加速度都为零,则由捷联惯导的比力方程可得:

式中, fb(t)为加速度计测得的比力,gn(t)为重力矢量。将式(1)带入式(3),并且等式两边同乘可得:
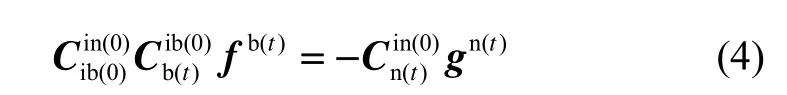
2 四元数估计算法
由上一节分析可知,捷联惯导初始对准问题已经转化为根据观测矢量求取姿态阵的问题。利用观测矢量确定载体姿态的Wahba问题是指最优姿态阵A的估计值应使如下损失函数达到最小:



式(6)可知损失函数 L(A)最小即使增益函数 g(A)取最大值。 g(A)可化为关于四元数q二次型函数:

式中,q为姿态阵A对应的四元数,K为4×4维矩阵:

式中,

考虑到约束条件 qTq= 1,根据拉格朗日数乘法,经推导可得出:使 g(q)达到最大值的四元数就是矩阵K最大特征值 λmax所对应的特征向量,即最优四元数qopt满足

式中,qopt= [q0qv]T,q0为四元数的标量部分,qv为其矢量部分。式(12)进行矩阵运算可得如下两式:
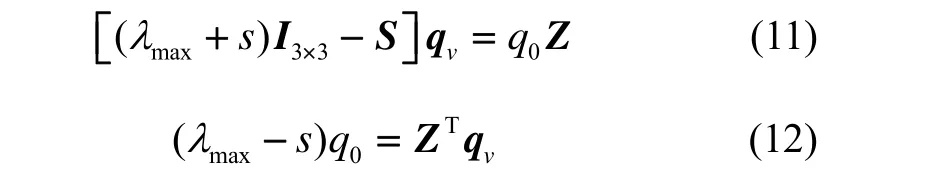
由式(11)可得:

则姿态阵对应的最优四元数为:

式中,

由式(14)可知只要求得 λmax,便可以确定 qopt。将式(13)代入式(12)可得 λmax满足如下四次方程:

直接解式(16)较为复杂,可使用牛顿迭代法求 λmax:
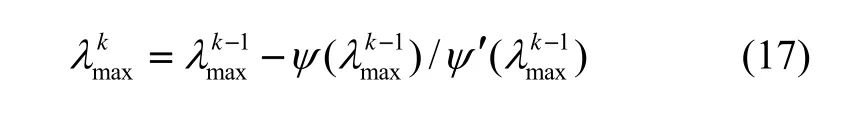
由文献[9]分析可知, λmax的值近似等于非负权值的和 λ0,即有:

因此, λmax的迭代初值应设置为 1。在实际应用中,由于 λmax的值十分接近 λ0,所以只需要进行一次迭代就可以得到满足精度要求的结果[10]。在得到 λmax后,根据式(13)便可以求出载体初始时刻姿态的最优四元数解 qopt。
3 摇摆基座抗干扰对准算法
3.1 干扰加速度的抑制
根据第1节的对准方案,同时运用第2节中的四元数估计算法,理论上可以有效隔离载体角运动的干扰并获得姿态阵的最优估计值。但在实际环境中,由于载体的线振荡、加速度计臂杆效应等干扰因素的影响,晃动基座下加速度计真实的输出在ib(0)系的投影应为:

式中,▽b为加速度计零偏,δKA为刻度系数误差阵,δA为安装误差阵,为臂杆干扰加速度,为船体线振荡引起的干扰加速度。δKA、δA经标定以后可以进行补偿,但在实际应用中往往难以对进行精确建模并补偿,造成式(4)不再保持严格成立。如果忽略式(19)中这些干扰加速度的影响,仍然按照式(4)进行对准,将会引起的计算误差,最终影响对准精度。因此,保证对准精度的关键是如何抑制中的干扰加速度,从而提取较为纯净的重力信息重力矢量随地球自转在惯性系中围绕自转轴缓慢的转动,由此可知的变化周期为24 h。在实际的舰船、车辆等环境中,外界振荡干扰的频率都远大于地球自转周期,因此根据实际使用环境对进行频谱分析,并合理地设计数字低通滤波器就可以有效地抑制外界干扰的影响,从中提取较为真实的信息。考虑到数字低通滤波器的群延迟效应(IIR型滤波器还存在非线性相位畸变),需对和同时进行低通滤波,这样可保证式(4)仍然近似成立[10]。这里需要指出的是,惯性器件的常值误差(加速度计零偏和陀螺常漂)是无法从频域上与分离的,因此低通滤波器主要作用是抑制载体振荡所引入的干扰加速度的影响,而惯性器件误差对准精度的影响仍然存在。
3.2 非负权值的确定
四元数估计初始对准算法需对观测矢量进行单位化处理,则观测矢量选取为:

根据文献[11]中的结论, ai的取值如下式所示:


式中,矩阵B的初始值设为零矩阵。基于四元数估计算法的摇晃动座对准法流程图如图1所示。

图1 晃动基座四元数估计对准算法流程图Fig.1 Flowchart of quaternion estimation alignment algorithm on rocking base
4 实验验证
为验证本文算法的有效性,采用激光陀螺捷联惯导的车载实验数据进行了半物理仿真实验,其中激光陀螺精度为0.01 (°)/h,加速度计零偏为5×10-5g,采样频率为125 Hz。在实验过程中,待惯导系统静态对准完毕后,开启发动机、人员上下车等活动施加干扰,选取其中120 s的数据进行捷联惯导抗干扰初始对准仿真实验。由于无法取得载体真实的姿态信息,这里采用SINS/GPS组合导航系统的姿态输出作为基准来检验对准算法的效果,如图2所示。

图2 车辆姿态角Fig.2 Attitude of the vehicle
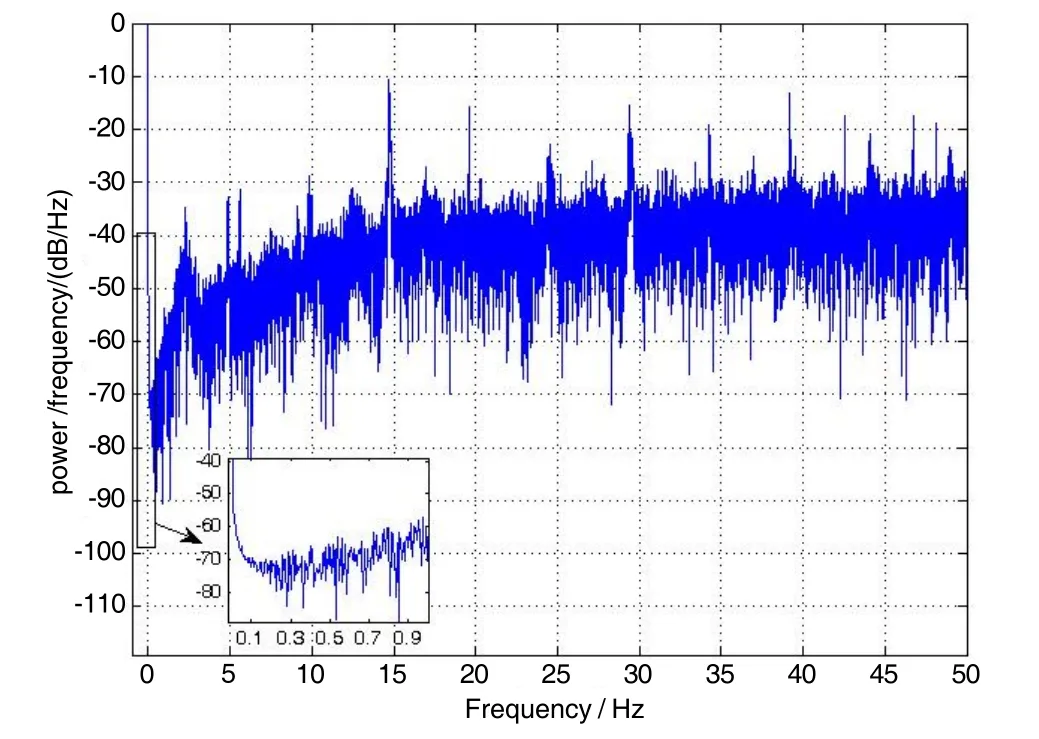
图3 X轴方向比力功率谱密度Fig.3 Power spectral density estimate of specific force along X axis direction
将以上选取的加速度计输出量转换到ib(0)系后,对其进行频谱分析,其中X轴方向比力信息的功率谱如图3所示,由局部放大图可以看出外部干扰加速度的频率主要集中在0.1 Hz以上的频段,从Y轴和Z轴方向比力的谱分析可以得到相似的结果。为减少计算量,采用阶数较低的IIR数字低通滤波器对三个轴向的比力信息进行滤波处理,滤波器的截止频率设定为0.1 Hz,导通频率设定为 0.005 Hz,则频率为1.1574×10-5Hz的重力加速度可顺利通过,同时可有效抑制频率高于0.1 Hz的干扰加速度信息。
分别采用Optimized TRAID算法和本文提出的四元数估计法进行初始对准,两种方法的对准误差如图4所示。随着对准时间的增加,两种对准算法的误差都逐渐减小;两者的水平姿态精度都较高,在 100 s以后达到5″以内。然而,由于Optimized TRAID算法只利用两个时刻的加速度计信息解算姿态角,而其余的观测信息实质上被丢弃,因而对准结果受到所选时刻观测量误差的影响较大。从图4中可以明显看出,与四元数估计法相比,Optimized TRAID法的结果具有较为明显的波动。四元数估计法的航向误差在第100 s后已经收敛到1.3′以内,而Optimized TRAID法的航向误差波动较大,航向误差约为 9.1′。试验结果表明,四元数估计对准法姿态角的收敛速度优于Optimized TRAID法,且航向角精度有较为明显的提高。
5 结 论
四元数估计对准算法实质上是根据观测矢量确定最优姿态。由于充分利用了对准期间所有的观测信息,估计出载体姿态在最小二乘意义下的最优姿态解。与基于双矢量定姿算法对准方法相比,它具有更快的收敛速度和更高的对准精度。实验结果表明,四元数估计对准算法可用于捷联惯导在晃动基座下的快速初始对准。
(References):
[1] White D, Psota F. A precision navigation system for
autonomous undersea vehicles[C]//IEEE. 1996: 262-267.
[2] 秦永元,严恭敏,顾冬晴,等. 摇摆基座上基于重力信息的捷联惯导粗对准研究[J]. 西北工业大学学报,2005,23(5):681-684.
QIN Yong-yuan, YAN Gong-min, GU Dong-qing. A clever way of SINS coarse alignment despite rocking ship[J]. Journal of Northwestern Polytechnical University, 2005, 23(5): 681-684.
[3] 孙枫,孙伟. 摇摆基座下旋转捷联惯导系统粗对准技术研究研究[J]. 仪器仪表学报,2010,31(4):929-935.
SUN Feng, SUN Wei. Research on coarse alignment of rotary SINS on swing base[J]. Chinese Journal of Scientific Instrument, 2010, 31(4): 929-935.
[4] Lee Seon-Ho, Ahn Hyo-Sung, Yong Ki-Lyuk. Three-axis attitude determination using incomplete vector observations[J]. IEEE Transactions Industrial Electronics, 2012, 59(11): 4465-4474.
[5] Bar-itzhack I Y, Harman R R. Optimized TRAID algorithm for attitude determination[J]. Journal of Guidance, Control and Dynamics, 1997, 20(1): 208-221.
[6] 王勇军,徐景硕,盛飞,等. 基于最优三轴姿态测定算法的舰载惯导粗对准方法[J]. 中国惯性技术学报,2013,21(2):294-297.
WANG Yong-Jun, XU Jing-Shuo, SHENG Fei, et al. Coarse alignment method based on optimized three-axis attitude determination algorithm for shipboard SINS[J]. Journal of Chinese inertial Technology, 2013, 21(2): 294-295.
[7] Wahba G. A least squares estimate of spacecraft attitude[J]. SIAM Review(S0036-1445), 1965, 7(3): 409.
[8] Shster M D, Oh S D. Three-axis attitude determination from vector observations[J]. J. Guidance and Control, 1981, 4(1): 70-77.
[9] Markley F L, Mortari D. How to estimate attitude from vector observations[J]. Advances in the Astronautical Sciences, 2000, 103(3): 1979-1996.
[10] 严恭敏,白亮,翁浚,等. 基于频域分离算子的 SINS抗晃动干扰初始对准算法[J]. 宇航学报,2011,32(7):1486-1490.
YAN Gong-min, BAI Liang, WENG Jun, et al. SINS anti-Rocking disturbance initial alignment based on frequency domain isolation operator[J]. Journal of Astronautics, 2011, 32(7): 1486-1490.
[11] Markley F L, Mortari D. Quaternion attitude estimation using vector measurements[J]. Journal of the Astronautical Sciences, 2000, 48(2): 359-380.
捷联惯导晃动基座四元数估计对准算法
高 薪1,卞鸿巍1,傅中泽2,张礼伟2
Alignment algorithm based on quaternion estimator for SINS on rocking base
GAO Xin1,BIAN Hong-wei1,FU Zhong-ze2,ZHANG Li-wei2
(1. College of Electricity Engineering, Naval University of engineering, Wuhan 430033, China;2. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China)
An alignment algorithm based on quaternion estimation (QUEST) is introduced to solve the alignment problem of SINS on rocking base. The solution of initial attitude matrix is transferred into a Wahba problem, i.e. determining the attitude from vector observations. The quaternion estimation algorithm is employed to estimate the optimized initial attitude-quaternion in the least-squares sense. The basic principle of quaternion estimation is given, and the solution of a quaternion estimation alignment algorithm for SINS on rocking base is presented. The results of vehicle tests show that the quaternion estimation algorithm can achieve faster convergence speed, compared with the alignment algorithm based on the double-vector attitude determination theory. Furthermore, the attitude accuracy is further improved, and the errors of horizontal attitude and the heading error are within 5″ and 1.3′ respectively in 120 s by using the quaternion estimation algorithm.
SINS; rocking base; initial alignment; Wahba problem; quaternion estimation algorithm
高薪(1982—),男,博士研究生,研究方向为导航、制导与控制。Email:xiaomaolv82@126.com
1005-6734(2014)06-0724-04
10.13695/j.cnki.12-1222/o3.2014.06.005
U666.1
A
2014-07-16;
2014-11-27
预研项目:航空科学基金资助项目(920120816001)
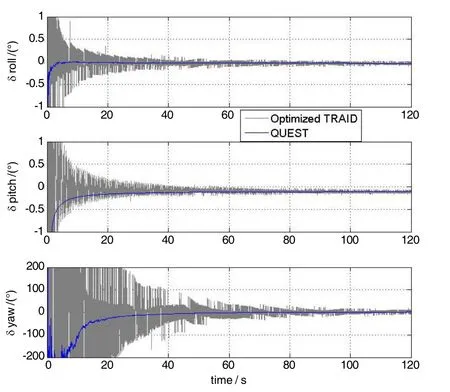
图4 两种对准算法姿态误差对比Fig.4 Comparison of attitude errors between the two alignment algorithms
