低成本车载MEMS惯导导航定位方法
2014-10-21清华大学自动化系北京100084
(清华大学 自动化系,北京 100084)
(清华大学 自动化系,北京 100084)
当GPS卫星信号受到遮挡,车载GPS无定位输出时,通过低成本MEMS惯导进行定位是车辆导航的一种弥补方法。然而低成本MEMS惯导测量误差大,定位误差会快速累积。针对此问题,研究了一种应用于MEMS惯导导航定位的Kalman滤波算法。通过分析车辆的运动特性,在已有的研究基础上,提出了向心加速度差值误差这一新型观测量,并推导了误差状态系统模型的状态转移矩阵和观测矩阵。200 s时长的实车实验表明,单纯MEMS惯导定位的误差率是75.27%,而所述新方法的定位误差率是3.86%,定位精度有了大幅度提高,取得了良好的效果。
MEMS惯导;车载导航;定位;Kalman滤波;向心加速度;观测量
GPS(Global Positioning System,全球定位系统)是目前在民用车辆上广泛使用的导航定位设备。GPS能够在地球表面绝大部分地区准确确定车辆的位置,为车辆提供路径导航等服务。GPS进行定位解算需要接收到至少4颗卫星的信号[1]。然而当车辆行驶到被树木或建筑物遮挡严重的道路、隧道、地下停车场等区域时,GPS不能接收到足够多的卫星信号来进行定位解算,这种情况下将没有定位输出,此时可以借助惯导设备进行推算定位。高精度惯导由于其价格高,难以应用于民用车辆。随着技术的快速发展,出现了低成本MEMS(Micro-Electro-Mechanical System,微机电)惯导产品,为民用车辆使用惯导设备创造了机会[2]。
MEMS惯导体积小、能耗低、价格低,但是其测量误差大[3]。一般来说,MEMS惯导设备价格越低,测量误差越大。使用低成本 MEMS惯导进行导航定位,其定位误差会随着时间增加而快速积累,在短时间内定位精度也较低,因而研究如何降低低成本MEMS惯导导航的定位误差,对于无GPS定位输出时的车辆导航定位具有积极意义。惯导导航定位降低误差的方法,通常是先建立适当的误差状态系统模型,再通过 Kalman等数据融合方法进行误差估计,最后根据误差估计对姿态、速度和位置进行校正[4-5]。当GPS没有位置和速度输出时,可用车辆坐标系横向和竖直方向的速度误差作为观测量[6]。然而仅通过此观测量进行状态估计后,定位精度仍有待提高。本文结合车辆的运动特性,提出了一种新的观测量,以进一步提高惯导导航定位时的定位精度。
1 定位算法
对于惯性导航系统,载体的姿态、速度和位置的变化率可以通过以下方程计算得到[7]:
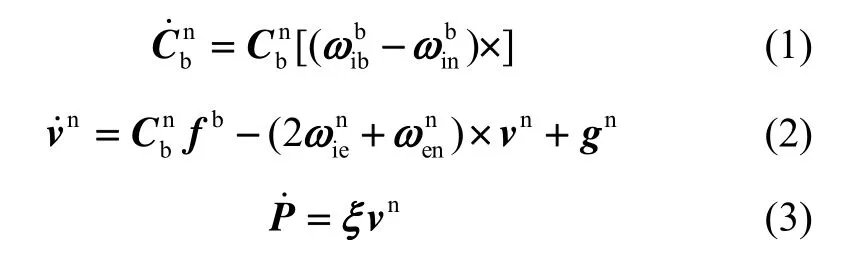
式中:v是速度矢量;P表示载体的位置矢量,P= [L λh]T,其中L、λ、h分别为纬度、经度和高度;f是比力矢量;g是重力加速度矢量;i、e、n、b分别是惯性系、地心地固坐标系、东北天导航坐标系和载体坐标系; ωie、 ωen、 ωib、 ωin分别表示坐标系e相对于i,n相对于e,b相对于i,n相对于i的旋转角速度矢量;上标n、b分别表示相应的值在坐标系n和b上的分解;是载体坐标系到导航坐标系的旋转矩阵,也称为姿态矩阵;表示的反对称矩阵;ξ是载体线速度到经纬度角速度的转换矩阵:
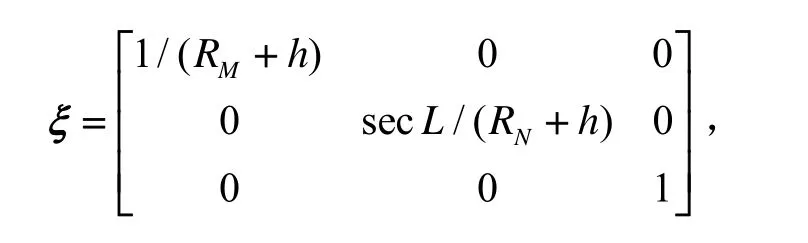
其中 RM、RN分别为当地子午圈和卯酉圈的曲率半径。
当初始导航参数已知,通过加速度计和陀螺仪可以获取 fb和,根据式(1)~(3)计算姿态、速度和位置的变化率后,再通过积分运算就可以计算得到载体的当前姿态、速度和位置。
2 误差传播
通过惯导输出的加速度和角速度数据来直接计算得到的姿态、速度和位置都含有误差[8]。计算值和真实值的关系如下:

在导航坐标系下惯导误差传播方程如下[8]:

式中, εg、 εa分别是陀螺仪和加速度计的测量误差,它们可以简化看作是一阶马尔科夫过程:

式中,τg、τa分别是 εg、εa的时间相关常数,wg、wa都是白噪声。
3 观测量
3.1 已有观测量
通常GPS/INS组合导航的观测量为GPS输出值和惯导计算值之间的差值,包括位置差和速度差。然而当GPS无有效输出,只通过惯导定位时,获取不了这些观测量。对于车辆运动,可以假设车辆不会发生侧滑,并且不会离开地面。设车辆载体坐标系如图1所示。
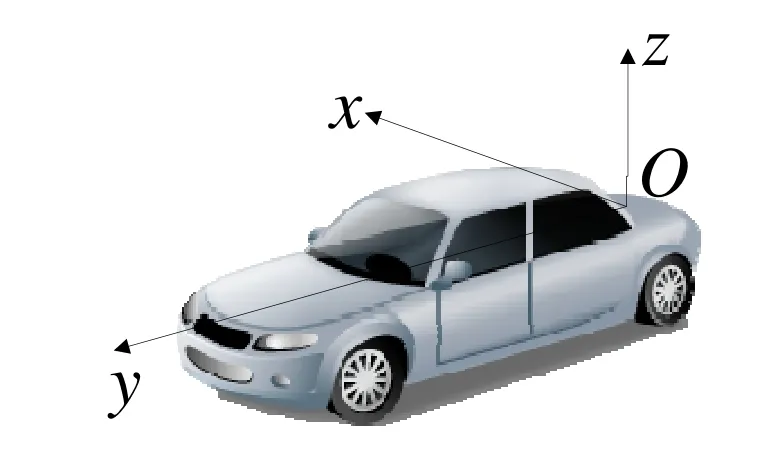
图1 车辆载体坐标系Fig.1 Vehicle body frame coordinates
载体坐标系的原点O位于车辆后轮轴中央上方一点,x轴平行于后轮轴指向车辆的右侧,y轴指向车辆前方,z轴垂直于x、y轴指向车辆上方。由于车辆不会发生侧滑,并且不会离开地面,则可以得到:车辆在载体坐标系x轴方向速度和z轴方向速度均为0,即

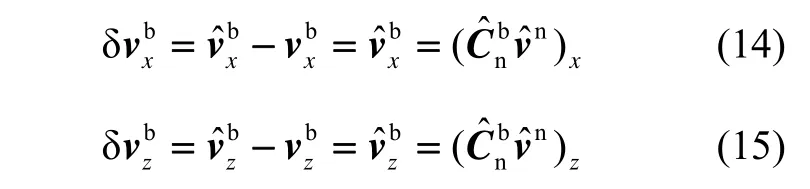
3.2 新观测量
大多数车辆的转向轮为前轮,当车辆转向行驶时,车辆的瞬时运动可以看作是围绕后轮轴线上一点为圆心的圆周运动[9]。当车辆直线行驶时,车辆运动也可以看作是曲率半径无限大的圆周运动。如图2所示,车辆载体坐标系原点O的速度方向与y轴平行,圆周运动的圆心P点在x轴轴线上。

图2 车辆圆周运动示意图Fig.2 Schematic diagram of vehicle circular motion
假设车辆在很短的时间dt内从A点移动到 A′点,移动的距离为dl,速度方向变化的角度为dφ,如图3所示。

图3 圆周运动细节分析Fig.3 Detail analysis of vehicle circular motion

根据圆周运动定律,可以推导得到向心加速度等于速度乘以角速度:

式中, ac为向心加速度。
设J为向心加速度差值,其通过下式计算:

根据方程(17)可得:



因为地球自转角速度和车辆线运动形成的相对于地球的旋转角速度相对较小,本文中将这两项角速度忽略,因而:
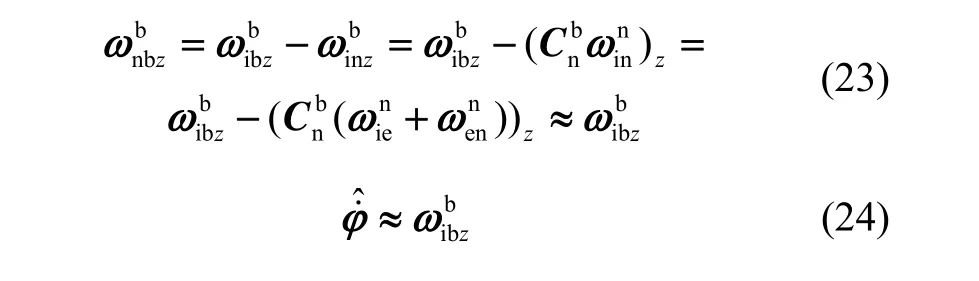


4 误差状态系统模型
通过扰动方程(18),可以得到J的误差方程:

式中, g0是当地重力加速度大小。
则可以建立误差状态系统模型,误差状态向量包含15个参数。系统误差向量X设为:

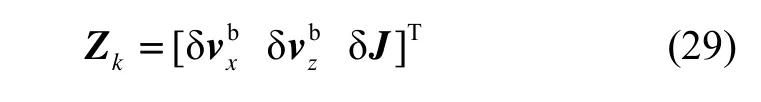
设离散化后的系统状态模型如下:
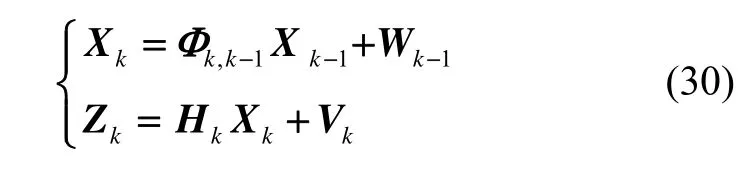
式中,Φk,k-1是15× 15维的系统状态转移矩阵; Hk是3× 15维的观测矩阵; Wk-1是过程噪声向量; Vk是观测噪声向量。设观测矩阵 Hk为:

矩阵 Φk,k-1、A的参数可参考文献[6][8]。根据误差方程(27),可以推导得到M矩阵,M中非零元素有:
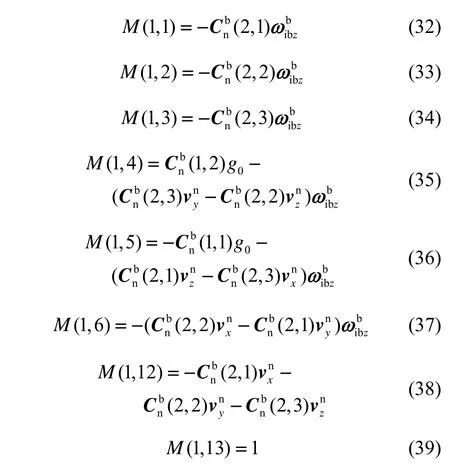
M矩阵的其余元素均为0。
建立好系统状态模型后,再根据 Kalman滤波的递推算法对状态进行估计。Kalman滤波递推算法可参考文献[11][12]。
5 实验验证
在清华大学内进行了实车实验。车辆上安装OxTS RT3100、MEMS惯导(Invensense mpu6050)以及bu353 GPS。RT3100是一款高精度GPS/IMU组合导航产品;mpu6050是低成本MEMS惯导,内置加速度计和陀螺仪,其价格约为3美元;bu353是一款低成本GPS,其价格约为30美元。RT3100和mpu6050的数据输出频率均设为20 Hz。各设备均安装于车辆后轮轴中间上方。RT3100输出的行车路线如图4所示。
RT3100内建高精度惯导,能够输出高精度位置、速度、姿态、加速度和角速度等数据。取一段RT3100的输出数据进行分析,该段数据采集时间为500 s,共有10 000个数据点。向心加速度的观测值及载体坐标系y轴速度与z轴角速度乘积的观测值如图5所示。
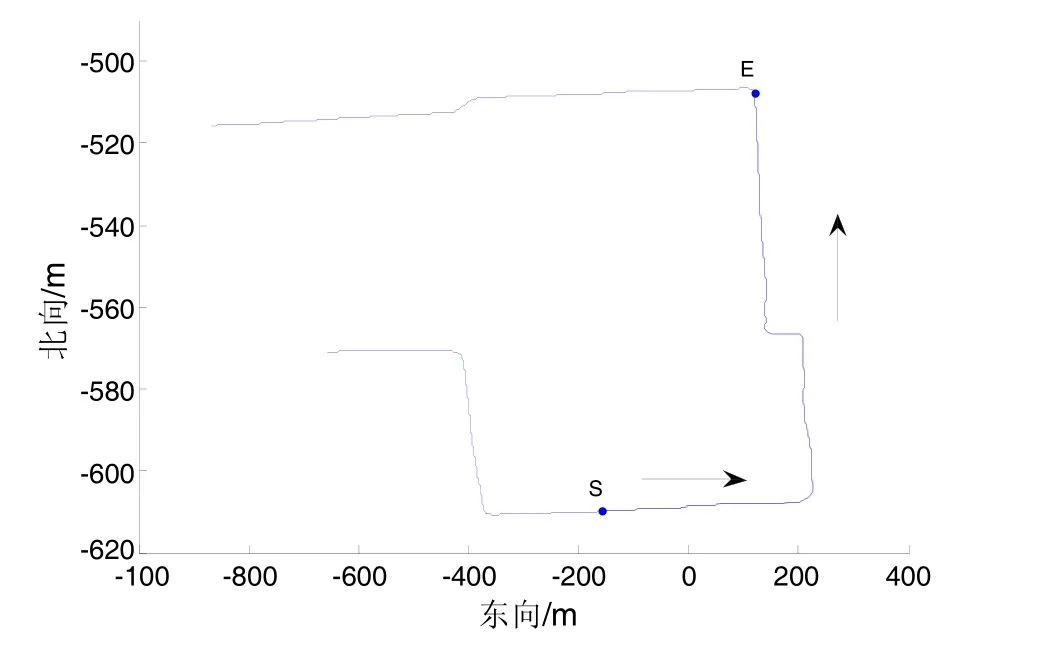
图4 车辆行驶路线Fig.4 Travel route of vehicle

图5 向心加速度观测值及载体坐标系y轴速度与z轴角速度乘积观测值Fig.5 Centripetal acceleration vs. y-axis velocity multiplied by z-axis angular velocity in body frame
从图4中S点位置时开始通过MEMS惯导导航定位,终点为E点。在车辆静止时测量得到mpu6050的各轴加速度和角速度零偏,以bu353在S点输出的位置和速度为初始值进行推算。通过以下3种计算方式进行定位:1)使用惯导数据直接推算;2)使用载体坐标系x轴、z轴方向上的速度误差作为观测量进行kalman滤波,称其为滤波 1;3)使用载体坐标系 x轴、z轴方向上的速度误差以及向心加速度差值的误差作为观测量进行Kalman滤波,称其为滤波2。
三种计算方式的定位结果如图 6。此间车辆行驶200 s,行驶总距离为1429.53 m,三种计算方式的最后定位误差如表1所示。
通过惯导输出数据直接推算定位在前10 s具有较好的准确度,然而由于低成本MEMS惯导测量误差较大,10 s之后出现了快速的发散,200 s时定位误差率达到75.46%。相对于直接推算,通过Kalman滤波进行定位的结果在200 s内准确性较好。滤波1的定位误差率为9.47%。增加了向心加速度差值的误差为观测量的滤波2定位误差率降为3.86%,定位精度有较大提高。

图6 3种计算方式的定位结果Fig.6 Positioning results of 3 kinds of calculations

表1 3种计算方式的最后定位误差Tab.1 Final positioning errors of 3 kinds of calculations
6 结 论
由于车辆行驶的区域可能被严重遮挡,车载GPS不能有效定位,此时通过惯导来进行车辆定位是一种较好的技术方法。从经济性方面考虑,低成本MEMS惯导可以普及应用于民用车辆。然而低成本MEMS惯导测量误差大,将其输出的原始数据直接用于导航定位,定位误差会随着时间增加而快速累加,难以直接用于车辆的定位导航。
针对此问题,本文研究了一种新式的MEMS惯导导航定位Kalman滤波算法。实车实验结果表明,使用本文所述方法后,定位精度有较大提高,取得了良好的效果。本文所提出的向心加速度差值误差这一观测量是通过惯导自身的输出计算得来,因而当惯导与GPS等其他定位方式组合用于对车辆导航时,其仍然可以作为观测量,将有助于进一步提高定位精度。
(References):
[1] 卡普兰,赫加蒂. GPS原理与应用(第二版) [M]. 寇艳红,译. 2版,北京:电子工业出版社,2007:39.
[2] Angrisano A, Petovello M, Pugliano G. Benefits of combined GPS/GLONASS with low-cost mEMS IMUs for vehicular urban navigation[J]. Sensors, 2012, 12(4): 5134-5158.
[3] Badri A E, Sinha J K, Albarbar A. A typical filter design to improve the measured signals from MEMS accelerometer [J]. Measurement, 2010, 43(10): 1425-1430.
[4] 谢钢. GPS原理与接收机设计[M]. 北京:电子工业出版社,2009:201-207.
[5] Noureldin A, El-Shafie A, Bayoumi M. GPS/INS integration utilizing dynamic neural networks for vehicular navigation[J]. Information Fusion, 2010, 12(1): 48-57.
[6] Sukkarieh S. Low cost, high integrity, aided inertial navigation systems for autonomous land vehicles[D]. Sydney:University of Sydney, 2000.
[7] 格里森,加布雷格齐亚布泽尔. GNSS应用与方法[M].杨东凯,樊江滨,张波,张敏,译. 北京:电子工业出版社,2011:108.
[8] 罗建军,马卫华,袁建平,岳晓奎. 组合导航原理与应用[M].西安:西北工业大学出版社,2012:68, 142.
[9] Bouron P, Crubille P, Meizel D. Data fusion of four ABS sensors and GPS for an enhanced localization of car-like vehicles[C]//2001 ICRA IEEE International Conference on Robotics and Automation. Seoul, Korea: 2001: 1597-1602.
[10] 米奇克,瓦伦托维兹. 汽车动力学[M]. 陈三荫,余强,译. 4版. 北京:清华大学出版社,2009:475.
[11] Simon D. Kalman filtering with state constraints: a survey of linear and nonlinear algorithms[J]. IET Control Theory & Applications, 2009, 4(8): 1303-1318
[12] 秦永元,张洪钺,汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安:西北工业大学出版社,2012:33-35.
低成本车载MEMS惯导导航定位方法
李博文,姚丹亚
Low-cost MEMS IMU navigation positioning method for land vehicle
LI Bo-wen, YAO Dan-ya
(Department of Automation, Tsinghua University, Beijing 100084, China)
When vehicle GPS has no positioning output due to GPS satellite signal’s being blocked, a positioning method based on low-cost MEMS IMU can be used to compensate the vehicle navigation. However, the measurement error of the low-cost MEMS IMU is large, and its positioning error would accumulate quickly. To solve this problem, a Kalman filtering algorithm for MEMS IMU navigation was studied. By analyzing the motion characteristics of vehicle, a new observation, i.e. the error of the centripetal acceleration difference, was presented. Then the state transition matrix and observation matrix of the error state system model were deduced. The real vehicle experiment for 200 s shows that the positioning error rate of autonomous MEMS IMU is 75.27%, and the positioning error rate by this new method is 3.86%, which show that the positioning accuracy has been significantly improved.
MEMS IMU; vehicle navigation; positioning; Kalman filter; centripetal acceleration; observation
1005-6734(2014)06-0719-05
10.13695/j.cnki.12-1222/o3.2014.06.004
TP23
A
2014-7-14;
2014-11-14
国家高技术研究发展计划(863计划)(2011AA110401)
李博文(1986—),男,博士研究生,研究方向智能交通系统。E-mail:libowen20@126.com
联 系 人:姚丹亚(1966—),男,教授,博士生导师。E-mail:yaody@tsinghua.edu.cn
