极点配置对SINS罗经对准性能影响

（1.西北工业大学 自动化学院，西安 710072；2. 航天科技集团 第16研究所，西安 710100）

（1.西北工业大学 自动化学院，西安 710072；2. 航天科技集团 第16研究所，西安 710100）

分析了罗经对准基本原理。基于常见的几种罗经极点配置方案及其对准性能与不足，将一个二阶振荡环节和一个临界阻尼环节相串联，把4个极点配置在同一个圆上，得到一种新的极点配置方案。该配置方法既保证了对准算法的快速跟踪性能，又兼顾对准精度。采用车载晃动对准数据和风扰条件下的车载导航数据，比较了不同极点配置的对准效果。试验说明，新的极点配置方案可以跟踪载体低频姿态角变化，在180 s内完成SINS对准过程；该方法能够克服大风扰动影响，提高SINS晃动基座对准精度。针对大失准角条件下的对准问题，通过相平面分析证明，罗经回路产生的非线性罗经驱动力矩同样可以将数学平台驱动到导航坐标系，实现大失准角条件下的快速对准。

捷联惯性导航系统；陀螺罗经；对准；极点配置；晃动基座

初始对准是捷联式惯导系统(strapdown inertial navigation system，SINS)应用中的一项关键技术。一般初始对准方法是根据地球的两个特征矢量——重力加速度g和地球自转角速度 ωie完成初始姿态的确定。但是在具体使用时，要考虑对准精度、对准时间、载体晃动情况等因素，采用不同的方法实现对准。文献[1]将基于参数估计的对准方法和Kalman滤波结合，把估计出来的速度误差作为观测量进行Kalman滤波，在载车发动机运转情况下，对准时间从原来的20 min缩短到8 min，精度与原来的Kalman对准算法相当；文献[2]和[3]讨论了非线性滤波在初始对准中的应用，取得较好效果，但是非线性滤波模型复杂，会导致计算量增加；文献[4]对陀螺和加速度计进行3级FIR滤波，虽然提高了惯性坐标系对准精度，但是滤波器造成的时间延迟达到 101 s，降低了动态适应性；文献[5][6]利用惯性坐标系作为过渡坐标系实现初始对准，但由于算法缺乏阻尼，只能通过对加速度积分或重积分的方法抑制干扰，对准精度受到限制。

与上述方法相比，罗经对准是最早出现的对准方法之一，同样可以很好地解决晃动基座的对准问题。国外学者对罗经对准进行了深入研究：文献[7]讨论了罗经对准在LINS中的应用，采用0.07 (°)/h (3σ)的激光陀螺在晃动基座上航向对准精度优于0.5°，对准时间20 min；文献[8]分析了纬度、惯性传感器误差、测量噪声、扰动特性等因素对定位精度 1 n mil/h的INS/GPS的罗经对准影响程度，并指出罗经对准作为惯性导航的核心技术，一直被众多科研机构和学者研究，但大多数公司将具体研究成果和技术细节作为内部报告不予公开。2000年后，随着激光和光纤陀螺精度不断提高，国内学者在 SINS罗经对准技术也投入了大量精力，但是从公开发表的文献中可以看出，国内学者对SINS的罗经对准性能的研究结论并不同一。例如：文献[9]认为大失准角条件下北向和东向回路存在较大耦合，罗经回路反馈量具有不确定性，该文在罗经回路中增加一个与航向角有关的系数，并通过一个开关在北向与东向通道之间切换罗经回路输入信号源，实现了大失准角条件下的罗经对准，仿真表明该改进算法可以不经过粗对准，直接进入精对准，对准时间300 s；文献[10]指出，SINS中的罗经方位对准时，不能在任意初始角度下实现对准，为了线性化方便,把方位角等分为四个象限，对准时根据方位角的区间范围确定不同的控制策略；文献[11][12]同样认为大失准角下不能对准，需要通过一定的改进措施才能使用；而文献[13]则认为罗经对准可以在任意大失准角条件下实现对准，不需要经过粗对准；文献[14]认为罗经对准时间很长，为了缩短对准时间，该文存储陀螺和加速度计的原始数据300 s，必须经过调平、粗对准、精对准等过程，重复使用这些数据4次才能完成罗经对准，这相当于需要1200 s对准时间。

以上研究结果表明，罗经对准在国内应用不是十分成熟，国内学者在其算法和性能方面还存在一定争议。本文从罗经对准基本原理出发，研究了不同极点配置的罗经对准性能，并提出一种新的极点配置方法。采用车载晃动基座对准数据，比较了不同极点配置的对准效果，给出了对准试验和跑车试验结果。试验说明，在晃动基座条件下，新的极点配置方法可以快速跟踪载体姿态变化，在180 s内实现SINS罗经对准，其对准精度可以达到理论对准极限精度。最后，针对大失准角条件下的对准问题进行了分析，指出罗经对准在大失准角条件下仍然可以实现对准，并给出了试验验证。

1 解析粗对准

SINS系统的对准一般包括两个阶段：解析粗对准和精对准。如果对准时间足够长，罗经对准完全可以不需要经过解析粗对准，直接进入精对准。如果希望在较短的时间内完成对准，减小罗经对准调节时间，则最好增加粗对准过程。

在解析粗对准阶段，SINS采集陀螺和加速度计的输出信息，通过解析计算，得到载体的粗略初始姿态矩阵。该姿态矩阵在一定的误差范围内，为下一步精对准做好准备。SINS静止时，加速度计的比力输出测量的是重力加速度矢量g在b系中的投影 -gb，陀螺角速度输出测量的是地球自转角速度矢量在b系中的投影。当对准地点的地理位置准确已知时，物理量g和 ωie在n系中的投影和也是已知的。由姿态矩阵可建立如下两个转换关系式：

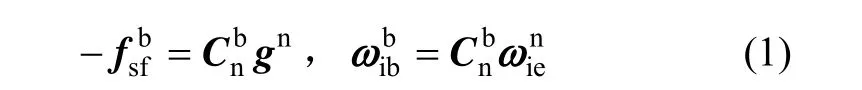
式中：gn=[0 0 -g]T，g为重力加速度大小；= [0 ωiecos LωiesinL]T，L为当地纬度，ωie为地球自转角速率。通过式(2)可求得初始对准姿态矩阵：

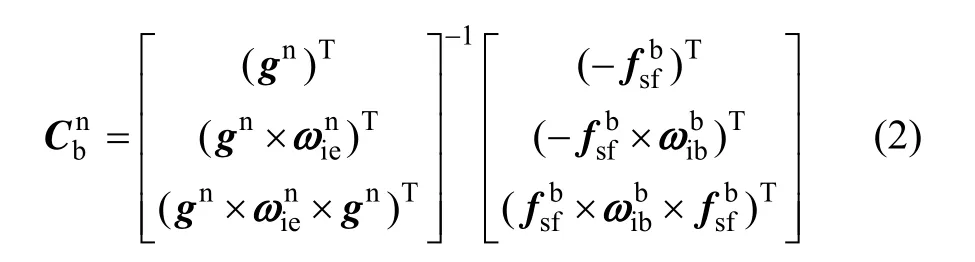
由于加速度计和陀螺测量存在噪声，通常采用一段时间内测量的均值和姿态矩阵最优正交化等方法提高对准精度。

2 SINS罗经对准

在罗经对准时，东向通道是独立的，完成北向水平对准，北向通道和天向通道耦合在一起，形成罗经回路，同时完成东向和天向对准，如图1所示。罗经通道通过对北向加速度计输出信号进行滤波处理，求得INS航向误差角的估计值，然后用这个估值经过加权形成指令信号，驱动物理平台（平台系统)或（捷联系统)转动到导航坐标系，从而完成精对准过程。

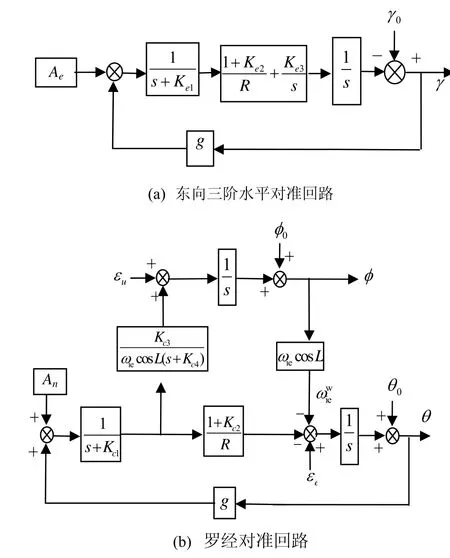
图1 罗经对准原理框图Fig.1 Gyrocompass principle

平台式 INS对准是通过电动机带动台体坐标系转动到导航坐标系并与之重合来实现的，罗经对准各个校正参数可以在理论上设计出来，但实际使用时必须考虑电源功率、电机最大输出力矩、摩擦力矩等因素影响，进行折中优化，这导致平台式INS罗经对准时间较长。而在SINS中，数学平台代替了物理平台，图1中的积分运算由姿态更新算法代替，对准框图转变为图2，图中Ke1、Ke2、Ke3、Kc1、Kc2、Kc3、Kc4是需要设计的校正参数。由于 SINS没有物理平台，而是通过姿态更新来实现数学平台的转动，设计参数时没有物理条件约束和摩擦力矩的限制，因此有可能通过优化参数设置，达到较好的对准效果。

罗经对准参数设计基本原则为：1）通过提高开环增益，增加系统刚度，降低稳态误差，提高对准回路的自然频率，从而保证在几分钟内，产生多次振荡调整；2）通过配置合理的极点位置，给对准回路提供适当阻尼，衰减振荡能量，尽快达到稳定状态。与其他控制系统校正问题一样，SINS罗经对准参数的选取也具有一定矛盾性：提高对准回路的自然频率意味着算法对准速度加快，带来的副作用是超调量也会增加；反过来，增大阻尼比会降低超调量，但会使调节时间增加。因此罗经对准参数设计时需要根据实际使用工况和指标要求进行调整，在精度和快速性质之间进行折中。国内学者针对罗经对准提出争议的根源在于不同的参数设计会导致对准性能大相径庭。在上述两条设计原则中，提高开环增益的目的明确，也容易理解，但试验表明，极点配置情况决定着罗经对准最终稳定时间，决定了罗经对准在晃动基座的对准精度。本文以下着重讨论罗经对准的极点配置方法。

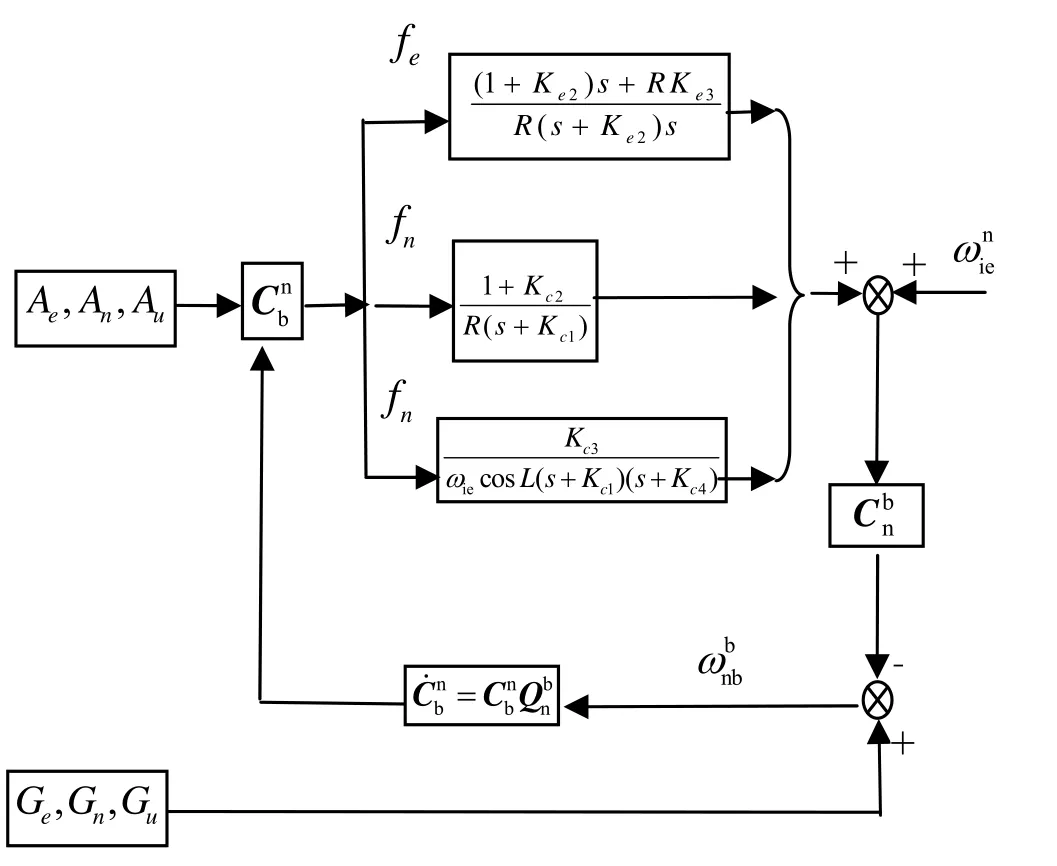
图2 SINS罗经对准信号流图Fig.2 Gyrocompass signal flowchart

3 罗经对准极点配置

根据图1(b)，由梅逊公式得到罗经回路的极点方程为：

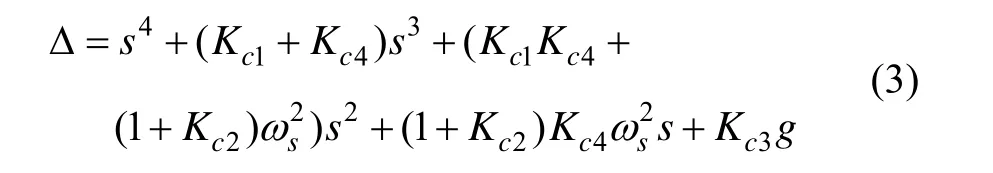
这是一个四阶系统，通常按照两个二阶系统串联来实现，常见的极点配置情况有三种情况：

1）双振荡环节串联

这是一种比较经典的设置方法[11]，假设罗经回路由两个相同的二阶振荡环节组成，极点分布图如图3(a)所示，则：

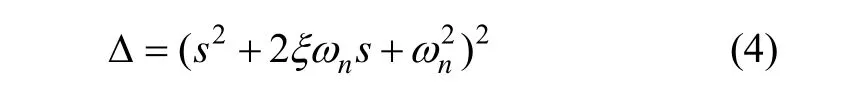
令式(4)与式(3)对应项相等得：

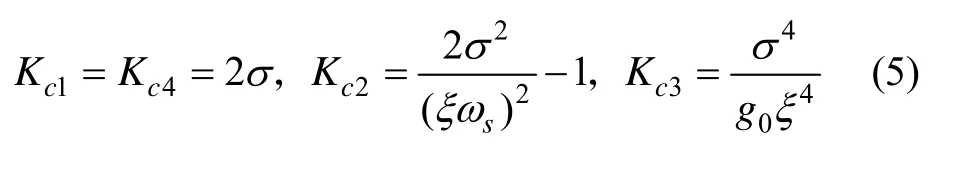
式中，σ为有阻尼振荡频率， ωs为舒拉角频率：

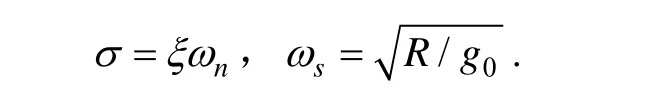
由于两个二阶系统都是振荡环节，在相同的阻尼比条件下，上升时间短，超调量大，稳态时对准结果波动性大，在晃动基座对准时会产生较大误差。

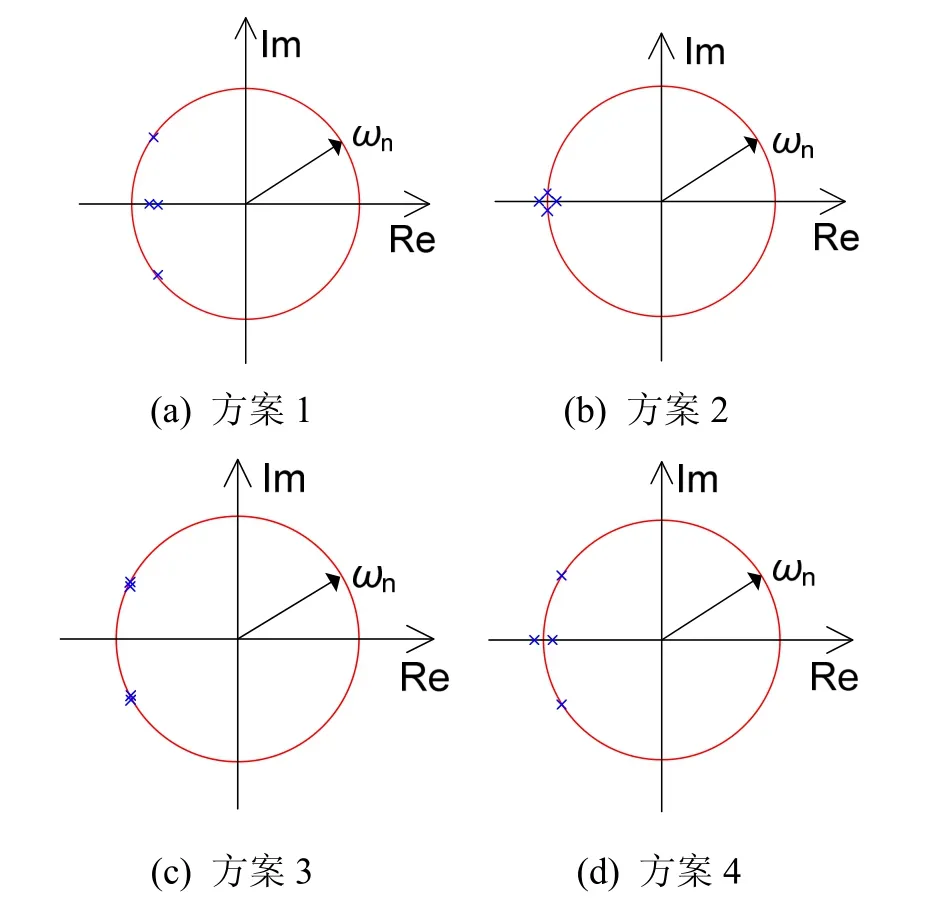
图3 不同极点配置方案Fig. 3 Different pole assignment schemes

2）双临界尼环节串联

假设罗经回路由两个相同的临界阻尼环节组成，极点分布图如图3(b)所示，则：

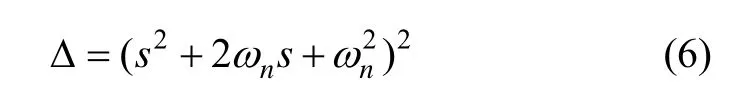
令式(6)与式(3)对应项相等得：

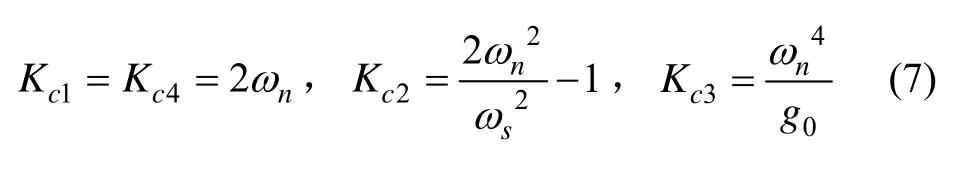
这种极点配置相当于第一种配置中 ξ=1的情况，阻尼比提高导致调节时间延长，跟踪载体姿态变化能力下降，稳态误差波动性下降，对准精度较高，适宜用于静基座对准，且对准时间有保证的情况。

3）一个过尼环节与一个振荡环节串联，四个极点拥有相同的实部

假设罗经回路由一个过阻尼环节与一个振荡环节串联组成，罗经回路的四个极点有相同的实部，过阻尼环节的极点在 ωn为半径的圆内部，极点分布图如图3(c)所示，则：

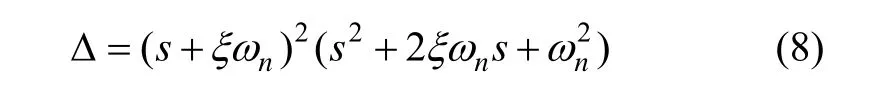
令式(8)与式(3)对应项相等得：

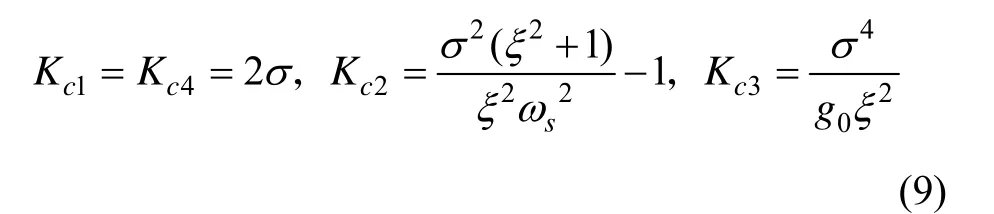
文献[12]采用了这种极点配置方法，引入过阻尼环节提高稳态精度，通过振荡环节提供较快的响应速度，在响应速度和稳态精度方面都有改进。

通过对极点配置的研究，作者提出了一种新的极点配置方法，其思路与第三种极点配置方法相同，仍然是一个过阻尼环节与一个振荡环节串联，但第三种配置方法中，负实轴上的两个极点在 ωn为半径的圆内部，而新的配置方法将两个实极点配置在以 ωn为半径的圆上，这样配置可以提供更大的跟踪能力，同时保证稳态阻尼，适合于晃动基座对准要求。设计结果如图3(d)所示。设：

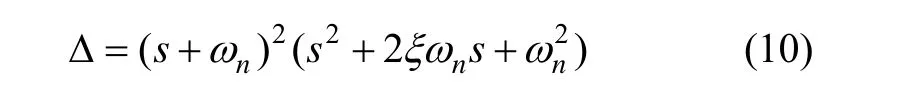
令式(6)与式(3)对应项相等得：

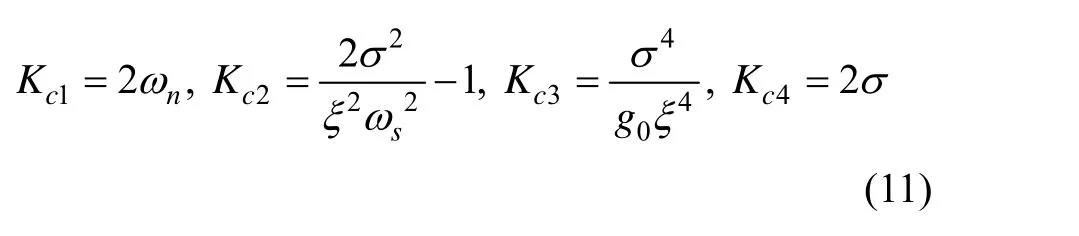
4 试验验证

4.1 不同极点配置晃动基座罗经对准试验结果

SINS在实际使用的初始对准过程中，载体往往不能完全静止，不论车载、舰载还是机载环境都会受到发动机转动、阵风、人员上下、装载货物等各种干扰因素的影响。大多对准算法都包含低通滤波环节，对这些扰动具有一定抑制作用，但由于算法不同，滤波参数不同，各种方法的滤波效果也不尽相同。为了提高对准精度，大量文献认为应该加强滤波，使用较低带宽的滤波器，将晃动引起的干扰尽可能的滤除。正是基于此观点，有学者对陀螺和加速度计原始数据设置额外的预滤波环节，为对准算法提供额外抑制扰动能力。例如文献[4]使用3级级联滤波器进行预滤波，将带宽压低到0.0125 Hz。这样尽量降低滤波器带宽的做法对 SINS初始对准一定好吗？答案是否定的。本文认为载体低频晃动时，姿态角的低频变化反应了载体真实运动，是一种有用信号，不应该把这些真实的低频信号滤除，否则数据虽然显得平滑，但已经不能反映载体的真实姿态角，反而造成对准误差。为了能让对准结果反应这种晃动，对准算法应跟踪载体这种低频运动，也就是说初始对准算法在数据处理时不应该过分滤波，而应保持算法对低频信号的敏感性。因此在罗经对准算法设计时，本文始终把极点配置对算法的跟踪响应速度作为一个重要指标，而不仅仅只考虑稳态精度问题。

本文采用一套激光捷联惯性导航系统(LINS)，陀螺漂移0.007 (°)/h，加速度计精度2×10-5g，进行了不同极点配置的车载对准试验。试验车为金杯商务车，试验条件分为：a）载车静止，2～3级微风情况；b）发动机开启，同时有5～6级风扰。做对准计算时，除极点配置不同，对准算法完全相同，其中阻尼比ξ取0.707，粗对准时间取2 s。

1）轻微扰动条件对准试验：图4和表1是第一种条件下的对准试验结果，对准时间300 s，对准时车头向北，横滚角和航向角通道构成罗经回路。尽管试验条件较好，但微弱的风扰也会使载车水平姿态角产生0.01°～0.02°左右的波动，这也说明水平姿态角对地面载体姿态扰动很敏感；不同极点配置对罗经回路的稳定时间有明显影响，极点配置方案1拥有最小的阻尼，上升时间最快，但在稳态时比其他三种配置方法波动大。方案2采用两个临界阻尼串联，曲线比方案1光滑，但跟踪能力差，不适合晃动基座对准。方案3和4的精度和跟踪载体姿态变化能力界于方案1与方案2之间，但方案4在跟踪速度上优于方案3，稳态精度与方案3相当。表1给出了最终对准结果，可见极点配置变化基本不影响两个水平对准结果。方案 2由于跟踪航向角变化速度慢，与阻尼最小的方案1相比，航向对准结果有0.024°的差异。方案3与方案4的对准结果比较接近，具有更高的可信度。从图2可以看出方案4在100 s左右即可进入稳定状态，因此采用这种极点配置，精对准过程可以在180 s内完成。

2）强烈扰动条件对准试验：试验选择在大风天气进行，风力5～6级，将试验车停放在公路旁边，测试数据时打开汽车发动机。由于公路上有大量汽车行驶，其速度约为 60 km/h，每当一辆汽车驶过，气流会对试验车造成冲击，车上试验人员可以感到车体明显晃动。

表2是最终对准结果，可见方案1和方案2的航向角最大误差为0.041°，大于试验(1)的0.024°，这与载体晃动幅度增加有关。图5是4种极点对准试验过程比较。在对准开始后15 s左右，有汽车驶过，导致横滚角和俯仰角分别产生0.02°和0.07°的摆动，同时气流冲击导致方案1和方案4的航向角产生0.07°的波动。方案3有0.03°的波动，而方案2的航向角基本没有因此产生波动，这进一步说明极点配置不同， 在动态对准时会有较大的精度差异。按照目前主流观点，方案2的波动最小，所以对准精度最高。然而事实并非如此，因为气流冲击的确导致车体姿态角发生了变化，这是一种有用信号，对准算法应该反应并跟踪这种变化而不是滤除。

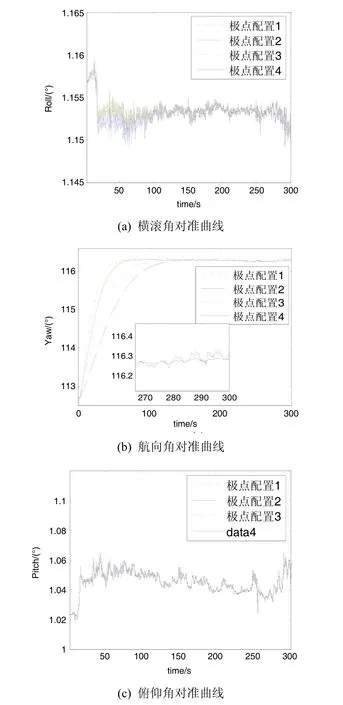
图4 轻微扰动条件下的对准过程曲线Fig.4 Alignment process in condition of slight disturbance

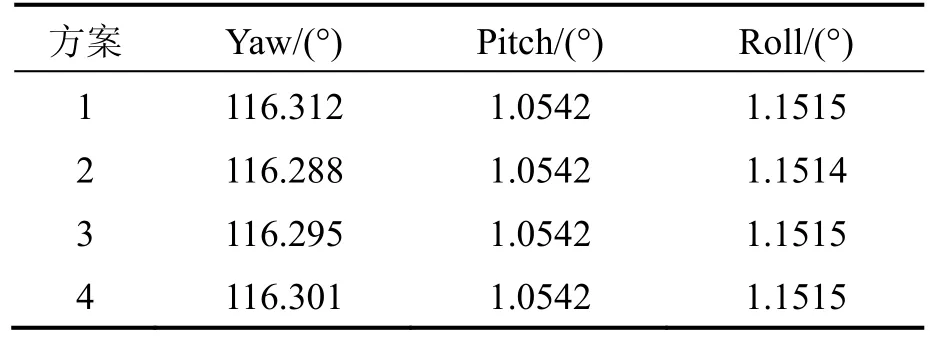
表1 轻微扰动条件下对准结果Tab.1 Alignment results when with slight disturbance

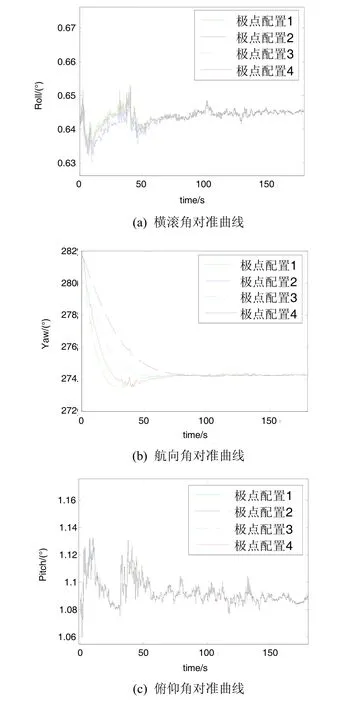
图5 强烈扰动条件下的对准过程曲线Fig.5 Alignment process in condition of strong disturbance

图6给出了四种方案对准后的导航结果，导航路线选择在西安市南郊附近一条“L”型路线上进行，试验路线的卫星地形照片见图6(a)。试验时在每一个标志点停车，记录GPS结果和LINS数据的时间标签，以便事后采用不同方法分析导航结果，跑车试验持续约5012 s，行驶里程62.5 km。

LINS 导航结果与随车携带的GPS导航结果比较见图6(b)，为了清楚起见，图中只在GPS和方案4对准后的导航结果上做出了标记点。从6(b)可以看出：初始阶段几种极点配置方法结果比较接近，随着时间增长，LINS定位误差逐渐增加。图6(c)和(d)给出了方案4对准后导航过程中载车的姿态和速度曲线。在每一个停车点，可以从图6(d)上看出车速为零。多次停车（特别是在试验后期的停车)引起的位置漂移增加明显，例如在4000 s左右停车时间约250 s，从图6(b)上看出，对应于该次停车，在倒数第3个标记点，LINS水平位置导航曲线出现一个“Z”字形拐点，导致位置误差漂移达到300 m以上。

表3则给出了不同极点配置方法对准后，水平导航定位误差。试验说明极点配置方案4的定位结果优于其他三种配置方法。

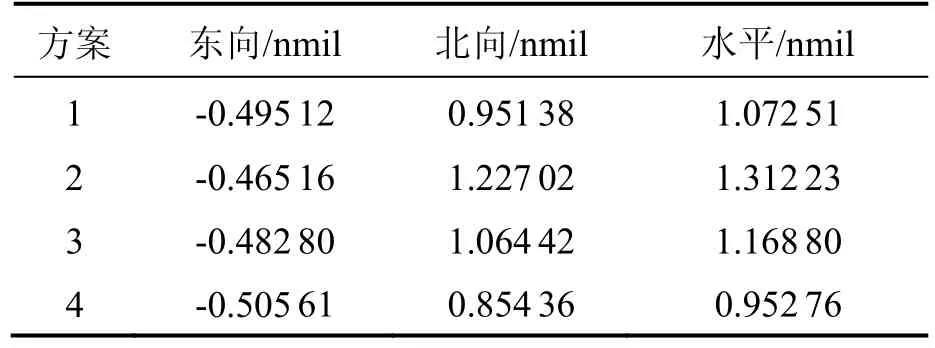
表3 不同极点配置对准跑车试验水平定位误差Tab.3 Level navigation errors of different pole assignment schemes

4.2 大失准角的罗经对准

罗经对准算法在大失准角条件下能否实现对准也是国内学者讨论的一个重要问题。文献[12]认为罗经对准是在小失准角条件下推导出来的，在大航向失准角的情况下，小角度的线性近似不成立。图1(b)中的罗经驱动力矩不再是= φωiecosL ，而是变成了=ωiesin φcosL ，因此无法实现大失准角对准。该文通过在罗经回路中增加非线性增益因子1/sinφ消除非线性，实现航向大失准角的对准。而本文认为罗经对准虽然在小角度下推导出来，但是同样适用于大失准角情况。因为罗经对准利用的是北向加速度计的漂移速率作为信号源，驱动物理平台的航向误差角φ向零逼近(平台系统)，或姿态矩阵向航向角真值逼近(捷联系统)。图 1(b)中，罗经回路只有一个稳定的能量极小值点——航向误差φ为零的平衡点。当φ为小角度时，这个驱动力矩近似为φ的线性函数；当φ不满足小角度条件时，这个驱动力矩是φ的非线性函数。与φ的相平面分析图见图 7，只要偏离这个平衡点，都会产生罗经驱动力矩。另外，在φ的定义域内的±180°也是平衡点，其罗经力矩也等于零，但这两个点是不稳定平衡点，微小的扰动即可使罗经回路偏离这两平衡点，一旦偏离这两个平衡点就会产生罗经力矩，进而驱动罗经回路最终回到φ=0的平衡点。因此，罗经对准可以不经改造地直接完成大失准角条件下的初始对准。只是由于大失准角条件下，罗经回路需要更多的调节时间，从而导致对准时间增加。

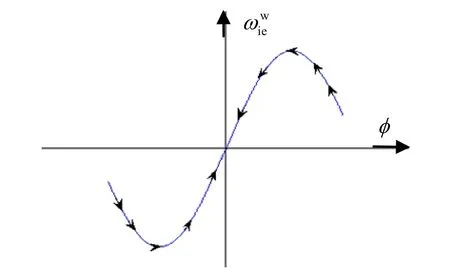
图7 大失准角罗经对准的相平面分析Fig.7 Gyrocompass alignment phase plane analysis under the condition of large azimuth misalignment

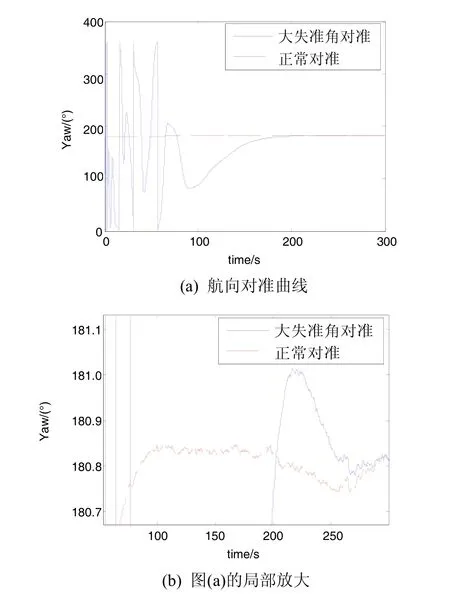
图8 大失准角条件下的罗经对准结果Fig.8 (Color online) Gyrocompass alignment results under the condition of large azimuth misalignment

为了验证本文观点，取一组车载晃动基座数据进行大失准角条件下的初始对准试验验证，结果如图 8所示。图8(a)中，红色虚线是正常对准条件下的（包含2 s粗对准）航向角收敛曲线，蓝色实线是将初始航向失准角置为 180°条件下的对准曲线，由图可见，经过几个周期的振荡，两条曲线基本重合。图8(b)是图8(a) 的局部放大，从图中可见：在200 s时，大失准角对准误差约为0.3°；在300 s时，两种对准曲线完全重合，对准结果仅有0.0019°的差异。因此，试验证明了本文观点的正确性。当然，为了减小大失准角条件下收敛较慢的问题，文献[11-12]提供了较好的思路，即采用变参数罗经对准算法，在对准前期提高对准速度，减小调节时间，在对准后期加强阻尼，降低稳态误差。

5 结 论

罗经对准方法具有算简单，不必事先建立数学模型，对准精度高等优点，在平台系统和捷联系统中大量应用。本文针总结了不同极点配置下的对罗经对准参数计算方法，综合考虑快速性和精度问题，提出了一种新的极点配置方案。车载晃动对准试验和跑车试验说明，使用该方案可以在180 s完成SINS的精对准；即便在大失准角条件下，罗经对准也可以不加修改地直接用于大失准角条件下，在300 s内完成对准。当然，在实际使用时，作者并不建议取消粗对准直接进入罗经对准，因为正如本文几组试验结果，即便通过2 s的粗对准，也会使罗经对准最终收敛时间大为缩短。

（

)：

[1] Li Qian, Ben Yueyang, Zhu Zhongjun, et al. A Ground fine alignement of strapdown INS under a vibrating base[J]. The Journal of Navigation, 2013, 66: 49-63.

[2] Acharya A, Sadhu S, Ghoshal T K. Improved selfalignment scheme for SINS using augmented measure- ment[J]. Aerospace science and technology, 2011, 15(2): 125-128.

[3] Zhou Zhanxin, Gao Yanan, Chen Jiabin. Unscented Kalman filter for SINS alignment[J]. Systems Engineering and Electronics, 2007, 18(2): 327-333.

[4] Lian Junxiang, Hu Dewen, Wu Yuanxin, et al. Research on SINS alignment algorithm based on FIR filters[J]. Journal of Beijing Institute of Technology, 2007, 16(4): 437-442.

[5] Verma V S, Sitara B, Kumar B R, et al. Novel method for coarse alignment of strapdown INS on oscillatory base[J]. Journal of Aerospace Sciences & Technologies, 2009, 61(1): 194-200.

[6] Li Wanli, Wu Wenqi, Wang Jinling, et al. A fast SINS initial alignment scheme for under water vehicle applica - tion[J]. The Journal of Navigation, 2013, 66: 181-198.

[7] Reddy N S, Murray J. Transfer obit stage gyrocompass alignment algorithm twist and sway environment for Mars observer mission on commercial Titan[J]. IEEE AES Magazine 1991(2): 3-7.

[8] Cuong Hua. Gyrocompass alignment with base motions: results for a 1 nmi/h INS/GPS system[J]. Navigation, 2000, 47(2): 65-74.

[9] 袁保伦，饶谷音. 惯导系统大方位失准角下的初始对准探讨[J]. 航天控制, 2009, 127(2):11-17.

YUAN Bao-lun, RAO Gu-yin. Study on the initial alignment of INS under large heading uncertainty[J]. Aerospace Control, 2009, 127(2): 11-17.

[10] 魏宗康，牛冰. 捷联惯性导航系统动基座全方位初始对准方法[C]//惯性技术发展动态发展方向研讨会文集.北京, 中国惯性技术学会, 2011, 196-203.

WEI Zong-kang, NIU Bing. SINS initial alignment on sway base for all-azimuth-angle[C]//Inertial Technology Development Prospects Proseminar. Chinese Society of Inertial Technology, Beijing, 2011: 196-203.

[11] 翁浚，严恭敏，秦永元. 基于大失准角时变参数罗经初始对准算法[J]. 中国惯性技术学报，2012，20(4)：425- 429.

WENG Jun, YAN Gong-min, QIN Yong-yuan. Variable parameter gyrocompass alignment algorithm based on large error angle model[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 425-429.

[12] 郝燕玲，张义，孙枫. 航向大失准角下的罗经法对准研究[J]. 仪器仪表学报，2011，32(7)：1478-1484.

HAO Yan-ling, ZHANG Yi, SUN Feng. Research of gyro-compassing alignment for large azimuth misalignment[J]. Chinese Journal of Scientific Instrument, 2011, 32(7): 1478-1484.

[13] 吕少麟，谢玲，陈家斌. 激光陀螺捷联导航系统初始对准方法研究[J]. 火炮发射与控制学报，2008(3)：15-18.

Lü Shao-lin, XIE Ling, CHEN Jia-bin. Research on Initial Alignment of RLG SINS[J]. Journal of Gun Launch & Control, 2008(3): 15-18.

[14] Li Sihai, Yan Gongmin, Yang Pengxiang. A rapid initial alignment alogrithm based on strapdown gyrocompass [C]//2nd Materials Science and Information Technology. Xi’an, China, 2012: 1563-1567.

极点配置对SINS罗经对准性能影响

李汉舟1，潘 泉1，邓 麟2，王小旭1，张娟妮2

Pole assignment’s influence on alignment performance of SINS gyrocompass

LI Han-zhou1, PAN Quan1, DENG Lin2, WANG Xiao-xu1, ZHANG Juan-ni2
(1. School of Automation, Northwestern Polytechnical University , Xi’an 710072, China; 2. 16th institute China Aerospace Science and Technology Corporation, Xi’an, 710100, China)

By analyzing the several common pole assignment schemes in gyrocompass alignment, this paper puts forward a new pole assignment scheme, which adopts a series connection structure for a second-order oscillation link and a critical damping link. The four poles are set on the same circle, which can guarantee the algorithm’s tracking performance and alignment’s high-accuracy. The comparison experiment results about the different pole assignment schemes in gyrocompass alignment were shown by using the data of the rocking base. It suggests that the new pole assignment method can track the attitude change of the car, and the whole alignment process of SINS can be finished within 180 s. The vehicle navigation tests were conducted in 6 levels of windy weather. The test results indicate that the new pole assignment scheme can overcome the interference of the wind, and improve the precision of the SINS alignment. Finally, the phase plane analysis is employed which suggests that the gyrocompass alignment can be used under the condition of large azimuth misalignment since the gyrocompass loop can also produce nonlinear driving torque to push the mathematical platform into navigation coordinate. ce nonlinear driving torque to push the mathematical platform into navigation coordinate.

SINS; gyrocompass; alignment; pole assignment; rocking base;

1005-6734(2014)06-0711-08

10.13695/j.cnki.12-1222/o3.2014.06.003

U666.1

A

2014-07-11；

2014-10-16

国家自然科学基金重点项目（61135001）；国家自然科学基金青年项目（61203234）

李汉舟（1973—），男，博士，研究员，从事高精度惯性导航系统、数字信号处理、机器视觉等研究。

Email：mr_lihanzhou@sina.com