牛顿迭代算法在声场定位中的应用

刘 霞，吴 崧

武汉工程大学电气信息学院，湖北武汉 430205

0 引言

声场定位技术是确定声源相对于传感器的距离和位置的新技术，涵盖了语言科学、声学、信号处理、电子学等学科，有着诸多方面的应用.根据声音探测方式的不同，声音定位分为主动声定位和被动声定位两种方式［1］.主动声定位有发射、接收装置，譬如雷达［2］，使用雷达向外发射信号，然后根据回波的性质判断待测目标的位置.被动声定位，只有接收装置，是利用目标上的辐射信号进行定位，与主动声定位相比较，具有隐蔽性强、安全性高等特点［3］，是现阶段声音定位技术研究的热点.

声场定位系统主要是利用各个传感器接收声音信号，经过信号滤波、放大等手段对信号进行处理，然后根据声音信号到达各个传感器的时间延时差TDOA(Time Difference of Arrival，以下简称:TDOA)计算出声源相对于传感器的位置［4］.利用时间延时差计算具体位置的算法有多种，最简单的就是勾股定律，根据直角三角形三边关系，计算出声源相对于传感器的位置.但是该方法求解方程非常困难，精度不高.牛顿迭代算法是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法，主要针对方程不存在求根公式的情况.牛顿迭代算法是求方程根的重要方法之一，其最大优点是在方程f(x)=0的单根附近具有平方收敛，经过多次迭代，即可计算出结果［5］.

1 系统总体设计

1.1 声场定位系统的功能设计

本系统在一个矩形区域的4个顶角A、B、C、D分别设置1个传感器，矩形区域内部设置1个可任意移动的扬声器，如图1所示.

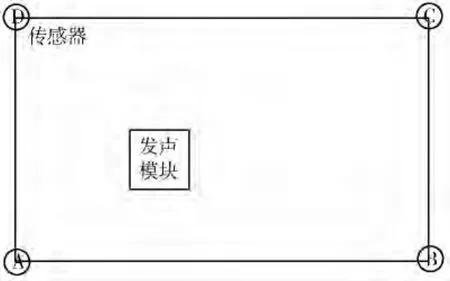
图1 系统结构图Fig.1 Structure diagram of system

发声模块发出特定频率的声音信号，传感器A、B、C、D接收到声音信号后进行信号滤波、放大等处理，单片机根据处理过的信号计算得到信号到达各点的时间差，再通过特定的算法，即可计算出声源在矩形区域中的具体位置.

1.2 系统基本原理

基于时间延时差的被动声音定位算法，其基本原理是在空间内，将4个传感器分别布置成一定的形状，来接收声源的声音信号，通过计算每相邻两个传感器之间所接收到的信号时间延时差，并结合所布置的声学阵列的几何关系，来计算得到声源位置坐标.如图2所示的示意图中，声源S的位置坐标为(x，y)，声源S到4个传感器之间的距离分别为 L1、L2、L3、L4.

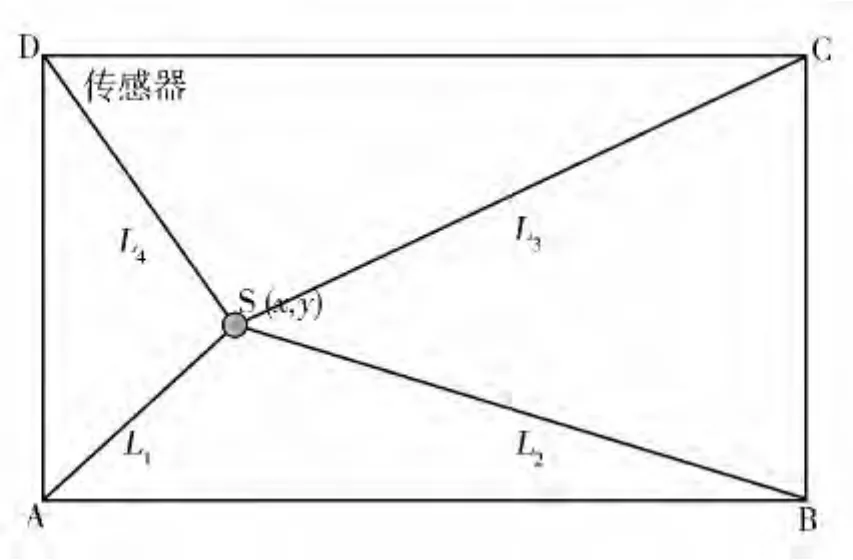
图2 系统坐标示意图Fig.2 Coordinate schematic diagram of system

2 算法设计

2.1 牛顿迭代算法

设xk是f(x)=0的一个近似根，把f(x)在xk处作泰勒展开可得:

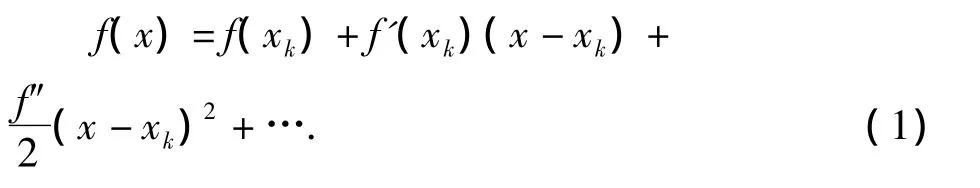
式(1)中若取前两项来近似代替f(x)，则得到近似线性方程:

利用上述方法，可以将牛顿迭代算法推广到二元函数，从而对系统的声源位置坐标求解.

2.2 声场定位中应用牛顿迭代法

当声源发声时，A、B、C、D点会根据声源S的具体位置按一定先后顺序接收到声音信号，例如点A先收到信号，则B和A之间的时间差为△T1，D和A之间的时间差为△T2.设A点为坐标原点，根据三角函数关系以及声音在空气中传播的时间与距离成正比的关系得到式(4)和式(5):

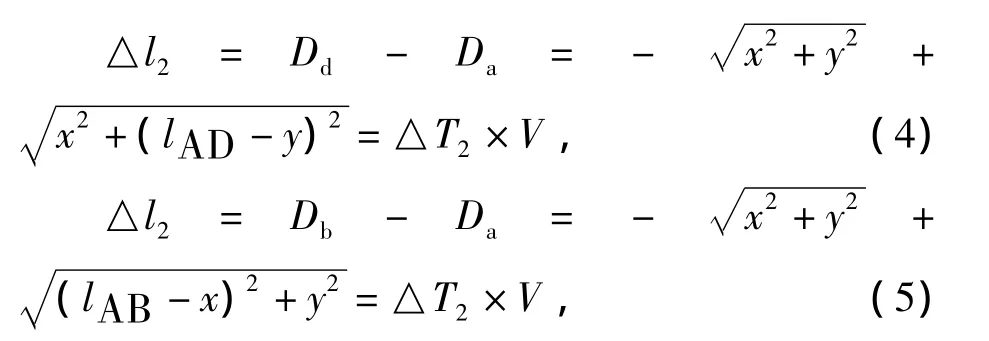
式(4)和式(5)中，V为声音在空气中传播的速度.设

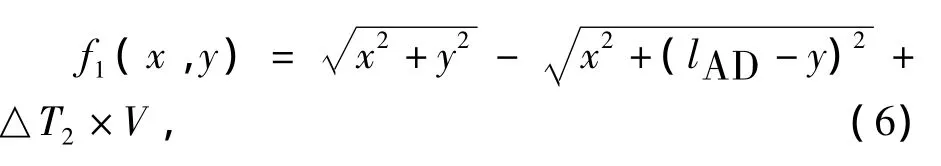
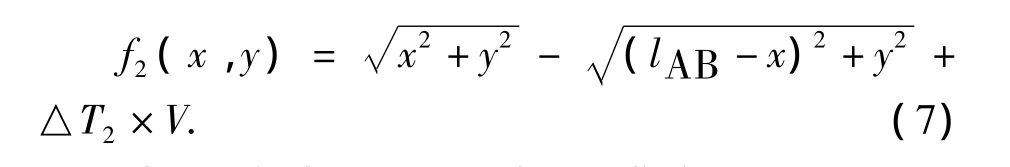
式(6)和式(7)分别对x，y求偏导数，得:

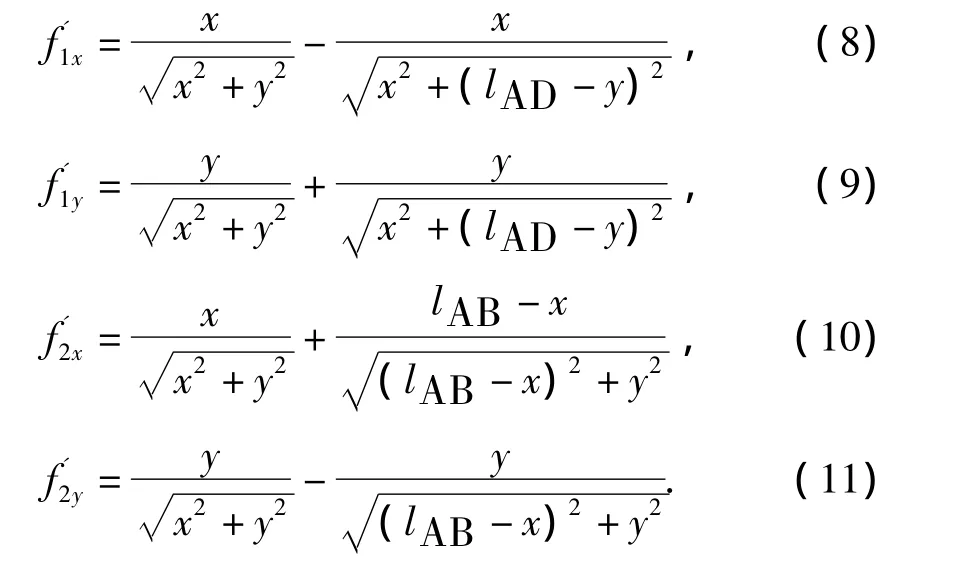
任取一点(x0，y0)，将式(6)和式(7)分别在该点处做泰勒展开，并取其一阶导数来近似代替f(x，y)，即 f(x，y)的线性化，得近似线性方程:

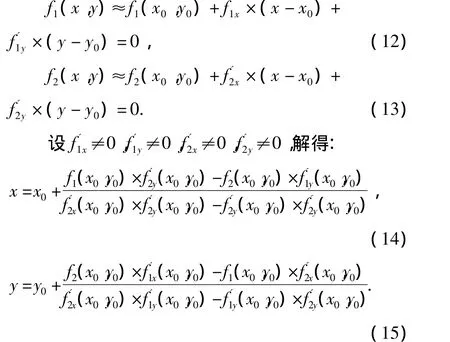
式(14)和式(15)，就是求解坐标的迭代公式.在求解过程中，(x0，y0)已知，可以计算出(x，y)的值，再将其带入以上两个方程，经过多次迭代运算，即可得到精确的位置坐标.

3 测试与分析

3.1 上位机测试

利用上位机软件可以很方便的测试牛顿迭代算法的可行性和精确性.编写的上位机软件界面如图3所示.

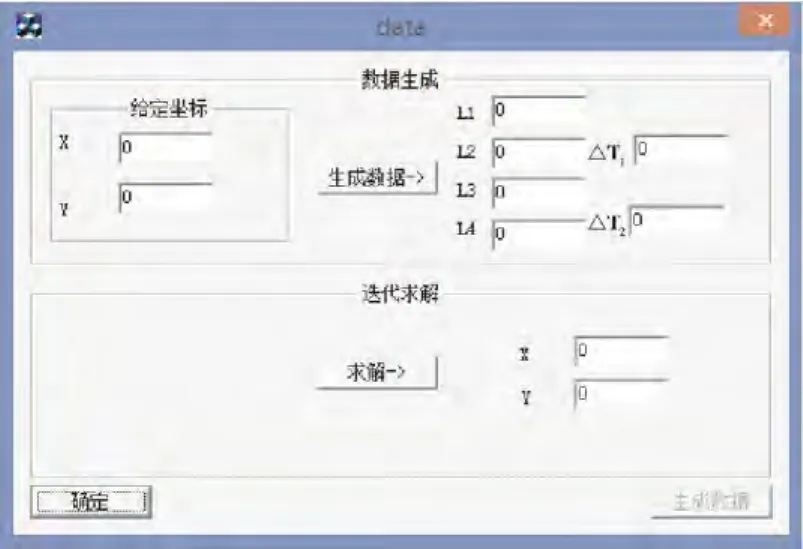
图3 上位机界面Fig.3 PC interface

由于是在上位机中进行模拟测试，所以需要设定S点到A、B、C、D点的距离数据和时间延时差△T1，△T2用于算法的测试.实验中，给定待测坐标为(30，80)，生成测试所需的数据为L1=85.44，L2=476.76，L3=542.033，L4=271.662，△T1=1.150 94，△T1=0.547 1.点击“求解”按钮进行迭代运算，位置坐标结果见表1.

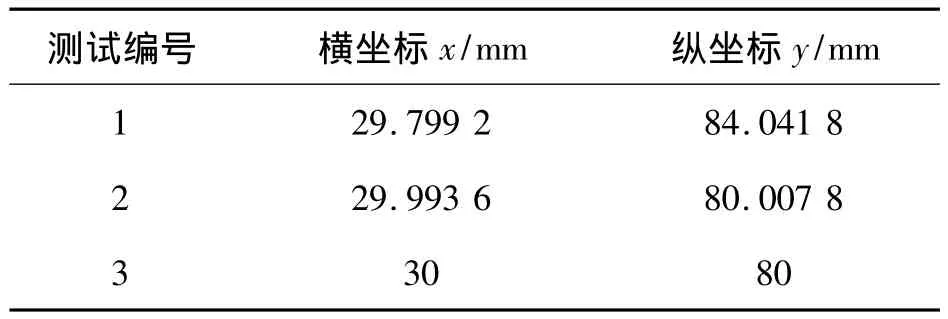
表1 上位机测试数据Table1 Test data of computer

从表1可以看出，只需经过3次迭代运算，即能精确得到待求的位置坐标，并且在第1次迭代运算时，得到的数据就已经非常接近实际值.

3.2 实物测试

在350 mm×500 mm的坐标纸上进行测试，传感器位于矩形区域的4个顶角，声源模块位于矩形区域内，让声源发出1 s左右的声音信号，单片机接收信号并进行运算.编写单片机程序用于实物测试，图4为系统软件流程图.

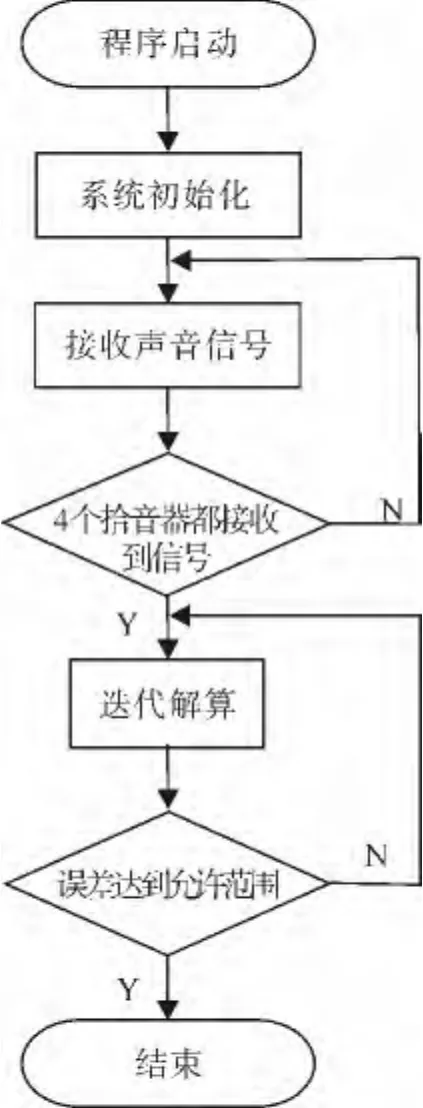
图4 程序流程图Fig.4 Diagram of program flow

经过多次试验所得结果如表2所示.

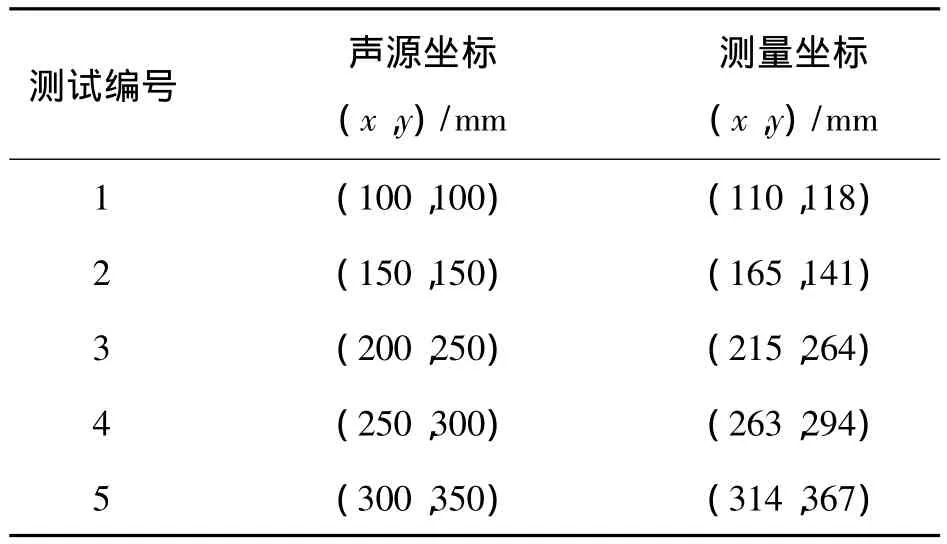
表2 实物测试数据Table 2 Test data

试验表明，系统能够可靠的实现坐标定位，但是略有误差.这种误差大多来源于传感器后级的信号处理，若4个信号处理部分不能完全一致，则时间延时差就不能准确测量，从而导致误差的存在.但是定位精度仍能达到±15 mm，可见定位性能稳定可靠.

4 结语

笔者提出了一套被动定位方式的声场定位系统，利用声音到达的时间延时差进行处理对声源进行精确定位.由于声音频率的局限性以及室内具体因素的影响，目前只能用在声音干扰小的环境且声源声音频率单一的情况.但系统采用的牛顿迭代算法，具有非常强的实用性.利用牛顿迭代算法的快速收敛性，在迭代过程中，只需要迭代几次就可以快速、精确计算得到声源坐标.上位机模拟测试和实物测试表明，牛顿迭代算法在声场定位中有着重要的应用价值.

［1］吴晓，靳世久，李一博.基于麦克风阵列声音信号定位方法的研究［J］.传感器技术学报，2010，5(23):682-684.WU Xiao，JIN Shi-jiu，LI Yi-bo.Sound source localiza-tion based on microphone arrays［J］.Chinese Journal of Sensors and Actuators，2010，5(23):682-684.(in Chinese)

［2］ADAMY D.Radar warning receivers:the digital revolution［J］.Electronics Defense，2000(6):45-49.

［3］肖峰，李惠昌.声，武器和测量［M］.北京:国防工业出版社，2002.XIAO Feng，LI Hui-chang.Sound，weapons and measurement［M］.Beijing:National Defence Industry Press，2002.(in Chinese)

［4］陈益如，王博，邬杨波.基于声音导引的声源定位系统设计［J］.工业控制计算机，2010，23(10):101-104.CHENG Yi-ru，WANG Bo，WU Yang-bo.Design of sound source localization system based on voice guidance ［J］.The Industrial Control Computer，2010，23(10):101-104.

［5］徐瑞民.二元非线性方程组求根的牛顿迭代法［J］.山东轻工业学院学报，2009，23(4):80-91.XU Rui-min.Newton’s method fourth-nonlinear function of two independent variables［J］.Journal of Shandong Institute of Light Industry，2009，23(4):80-91.(in Chinese)