基于全变差的超分辨率图像重建

王艳琴，吴爱弟，王 静

（天津职业技术师范大学理学院，天津 300222）

超分辨率图像重建技术是指利用已知的低分辨率图像信息采用软件方法来重建高分辨率的图像。根据已知低分辨率的信息，图像的重建方法可分为单帧图像的重建和多帧图像的重建。图像重建的好坏在于在提高分辨率的同时能否有效地保持图像的边缘及重要的纹理信息。图像超分辨率重建技术已被广泛应用于视频监控、地震勘探、卫星遥感遥测、医学成像、图像处理等领域中[1-4]。

在超分辨率图像重建算法中，最常用的也是最容易实现的是基于插值的算法，如最近邻域插值法、双线性插值法、双三次插值法等等。插值算法的优点是简单直观，且计算复杂度较低，但是本质上没有增加图像的信息，效果不是很理想。因此，经常与其他方法结合使用，如与小波变换方法一起使用[4]。文献[5]提出了一种基于小波变换的超分辨率图像的重建方法，先对低分辨率图像进行小波变换，然后在小波域上使用插值方法，再应用小波逆变换得到重建的超分辨率图像。

从数学角度理解，高分辨率数字图像的重建问题是一个代数反问题，由于已知条件不足该问题是个病态问题，直接求解效果不好，习惯采用正则化优化方法，将病态问题转化为良态问题，然后再进行求解。最常用的正则化方法是Tikhonov正则化法，重建的超分辨率图像的质量取决于正则化算子的设计及正则化算子的选择[6]。基于总变差的正则化函数可以很好地保持图像的边缘和细节信息[7-8]，较好地刻画图像空间，因此成为超分辨率图像重建方面研究的热点。本文根据低分辨率图像生成的矩阵模型，首先应用广义逆矩阵理论，得到高分辨率图像所在的解空间，然后把最小总体变差作为目标函数，应用最速下降方法求解，得到重建的高分辨率图像。

1 问题描述与数学建模

图像分辨率变低的原因主要是由光的扩散导致的运动模糊及物体在运动过程中的几何变形和受硬件条件的影响导致采样不足。将图像矩阵按列排列成一个向量，应用矩阵变换来模拟图像的生成过程，则被观测到的低分辨率图像可以用下列方程描述：

式中：y为已知的低分辨率图像；x为待求的高分辨率图像；F是几何变换矩阵；H是运动模糊矩阵；D是采样矩阵；n为随机噪音，可以假定它为高斯噪声。超高分辨率重建的目的是利用方程（1），从已知的低分辨率图像y估计出未知的高分辨率图像x。

一般地，方程（1）是病态的，故在求解方程（1）时，常做正则化处理，引入的正则化，约束求解空间，用于消除不适定性，将问题变为一个最优化问题，其数学模型为：

式中：第一项为数据保真项，表征了待估计图像与真实高分辨率图像之间的拟合程度；J（x）为正则化项，提供图像先验信息；λ为正则化参数，用于权衡两项之间的比重。

2 基于全变差的重建方法

先不考虑噪声影响，模型（1）可以写为：

式中：y为低分辨率图像；x为待求的高分辨率图像；A=DHF为已知。根据广义逆矩阵理论，方程（3）的通解为：

其中：z为任意向量。希望从这解集中找出所需的高分辨率图像。

根据文献[9]，可取A为一循环矩阵。由于式（2）中第一项已经为0，因此只要优化第二项即可。取z作为自变量，x由式（4）确定为z的函数，令

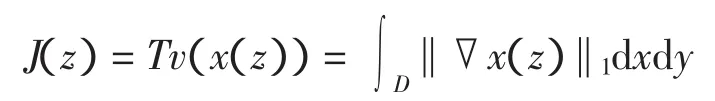
为图像x的总体变差，将解集中总体变差最小的解作为理想高分辨率图像。

对数字向量x，有

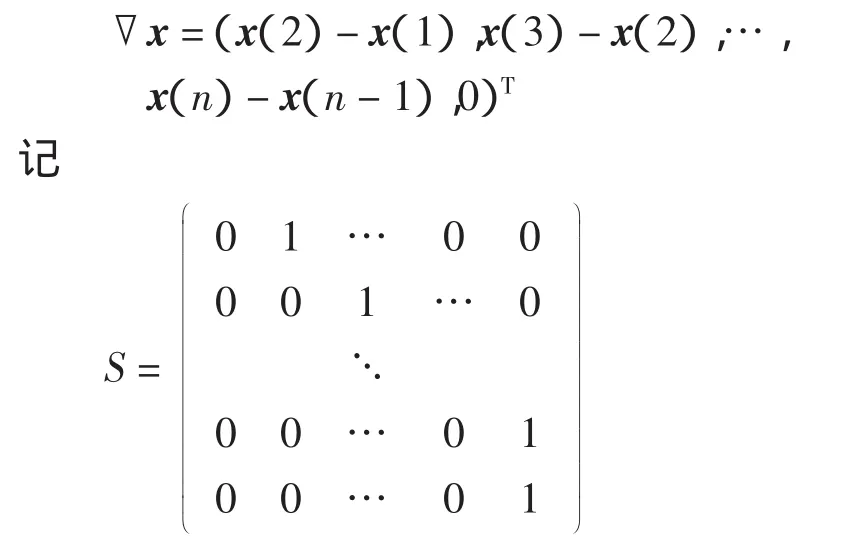
则▽x=Sx-x，将式（4）代入得

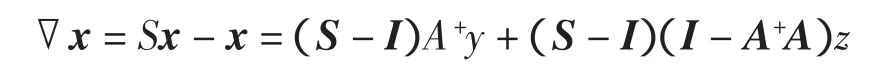
于是对一维的离散向量x，可取J（z）=‖▽x‖1，从而

算法1 优化问题J（z）=min，利用最速下降法迭代求解，其步骤为：

任选初值z0，对n=1，2，…

① 计算x=A+y+（I-A+A）zn；

③ 计算zn+1=zn- α▽J（zn）；

如果对图像x不写成向量形式，用矩阵方式进行处理。对x行列向量进行模糊下采样，则可以写成形式AxB=y，根据广义逆矩阵理论，其通解为：

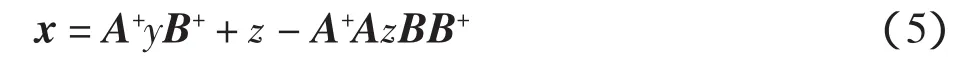
现选择z使得图像的总体有界变差J（z）=Tv（x）达最小，其对应的x即为重建的高分辨率图像。

引理1设f（x）=‖AxB‖1为矩阵函数，则

算法2 优化问题J（z）=min，利用最速下降法迭代求解，其步骤如下：

任选初值z0，一般选取零作为初值。

对n=1，2，…

①计算x=A+yB++z-A+AzBB+；

③ 计算zn+1=zn- α▽J（zn）；

3 数值实验

采用图像的峰值信噪比（PSNR）作为重建图像质量的指标。峰值信噪比越高，表示重建图像的质量越好。PSNR定义为：

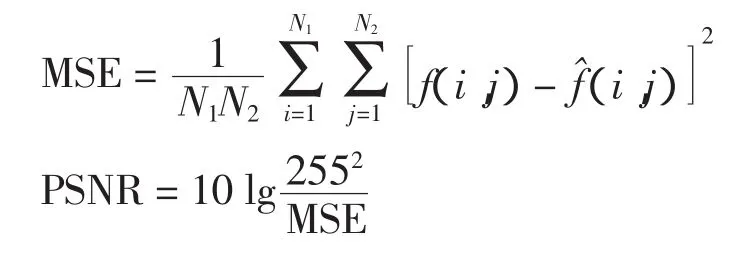
式中：f（x，y）和f^（x，y）分别表示原始图像和重建图像；N1和N2为图像的维数；MSE表示均方误差值。

对一元函数

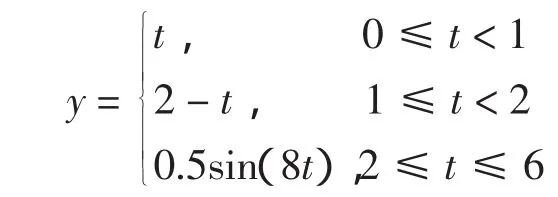
如图1（a），用平均值滤波加下采样生成低分辨率图形；图1（b），应用算法1得到重建的高分辨率图形；图1（c），均方误差为0.05。从图1可以看出，其线性部分的高频信息得到比较好的恢复，其周期部分也得到了不同程度的恢复。

图1 算法1的实验结果

对二维数字图像，采用Lena图像和Barbara作为测试图像，大小为512×512，用平均值滤波加下采样生成低分辨率图像，对有噪声的图像先应用小波阈值进行去噪处理[10]，然后应用插值方法和本文方法算法2重建高分辨率图像，其结果如图2、图3和表1所示。

图2 重建图像结果比较（无噪声情形）

图3 重建图像结果比较（有噪声情形）

表1 图像重建的峰值信噪比

由于采用最小变差作为优化目标，得到的高分辨率图像能较好地保留图像的边缘信息，重建的效果优于插值方法。

4 结束语

本文应用广义逆矩阵和总体变差思想，提出一种基于广义逆矩阵和变差的高分辨图像重建算法。首先利用广义逆矩阵理论得到高分辨率图像所在的解空间，然后把总体变差作为目标函数进行优化，采用最速下降算法进行求解，得到高分辨率图像。数值实验表明，该方法能较好地保留图像的边缘信息，重建图像的效果优于插值方法。

[1]MILANFAR P.Super-resolution Imaging[M].New York：CRC Press，2010.

[2]PARK S C，PARK M K，KANG M G.Super-resolution image reconstruction：A technical overview[J].IEEE Signal Processing Magazine，2003，20（3）：21-36.

[3]苏秉华，金伟其，牛丽红，等.超分辨率图像复原及其进展[J].光学技术，2001，27（1）：6-9.

[4]BOSE N K，LERTRATTANAPANICH S，CHAPPALLI M B.Super-resolution with second generation wavelets[J].Signal Processing：Image Communication，2004，19（5）：387-391.

[5]HONGJIU T，XINJIAN T，JIAN L，et al.Super-resolutionremote sensing image processing algorithm based on wavelet transform and interpolation[J].Proceedings of SPIE，2003，24（8）：259-263.

[6]路庆春.正则化超分辨率图像重建算法研究[D].合肥：中国科学技术大学，2010.

[7]占美全，邓志良.基于L1范数的总变分正则化超分辨率图像重建[J].科学技术与工程，2010，10（28）：6903－6906.

[8]朱高，王培康，宋慧慧.基于变差正则化的超分辨率图像重建[J].计算机工程，2012，38（17）：235-238.

[9]CHAN R，CHAN T，SHEN L，et al.Wavelet deblurring algorithms for spatially varying blur from high-resolution image reconstruction[J].Linear Algebra Appl，2003，366：139-155.

[10]DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory，1995，41（3）：613-627.