阳城电厂送出线路电压异常波动原因分析
2014-10-20隋佳音梁志峰
隋佳音,梁志峰
(1.国网电科院北京国电通公司,北京 100070;2.国家电力调度通信中心,北京 100031)
0 引言
随着全国互联电网的发展,电网稳定破坏、电压崩溃和低频振荡等问题日趋复杂,传统能量管理系统(EMS)已不能满足现代大电网动态监控的需要,迫切需要丰富监控手段,同步相量测量装置(PMU)是实现交流大电网相量分析的重要工具[1-2],特别是在实时监测系统运行状态和电网故障分析等方面表现突出。调度在实时监盘中发现,阳城电厂送出系统电压存在0.3~1.5 Hz的低频等幅振荡,采取提升母线电压或降低机端出力等措施对该振荡没有任何抑制作用。
1 问题描述
阳城电厂共8台机组,通过阳东(阳城电厂-东明站)3回线和东三(东明站-三堡站)3回线并入华东主网,上网功率为3000 MW。阳城电厂、东明站、三堡站母线电压分别为540,530,522 kV。
1.1 振荡情况统计
从电网动态监视中抽取现有历史数据进行统计分析。随机抽取2011年7—11月若干时间段的电压振幅、功率振幅并估测振荡频率,具体数据见表1(以阳东I线为例)。
1.2 各分量振荡曲线Prony分析
以2011年11月23日阳东I线的电压、有功功率、无功功率等振荡曲线为例,对阳东I线正序电压、各相电压、有功功率及无功功率进行Prony分析。统计信息见表2,其中阳东I线A相电压振荡曲线及其Prony分析如图1所示。
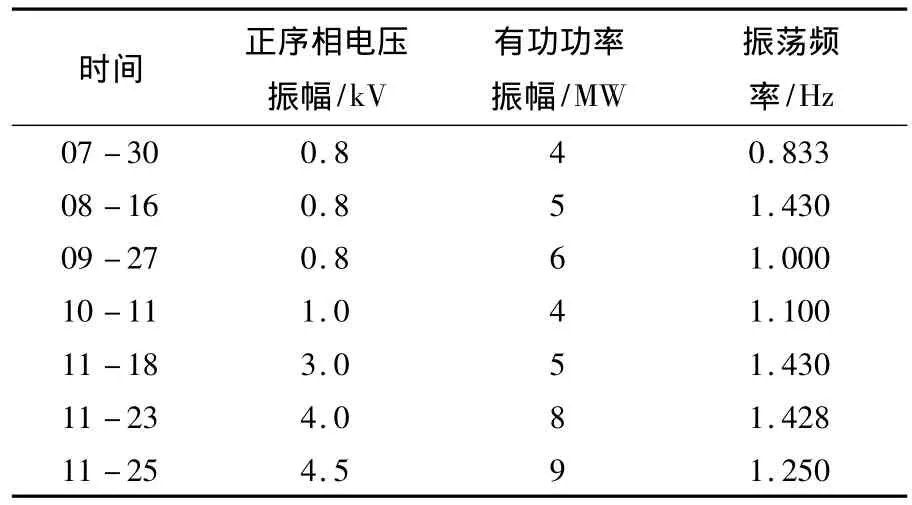
表1 2011年7—11月线路电压振荡统计
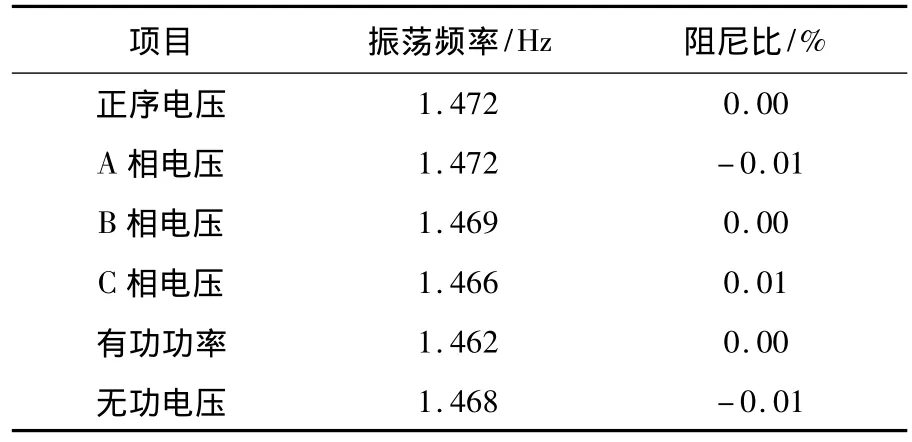
表2 各相量振荡曲线的Prony分析
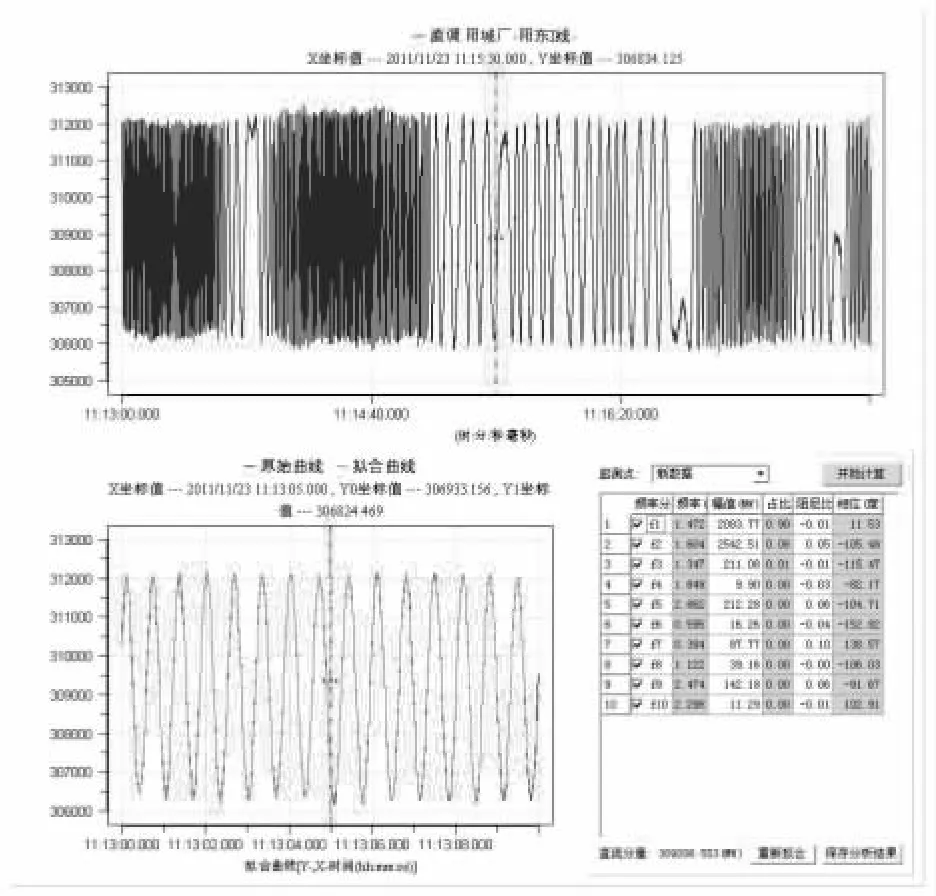
图1 阳东I线A相电压振荡曲线及Prony分析
1.3 各电气量振荡情况的主要特征
(1)线路正序电压振荡呈逐渐增大趋势。从表1可以看出,正序相电压振幅逐渐增大,从0.8kV增加到 4.5 kV。
(2)线路三相电压幅值、相角振荡特征不一致。线路A,B相电压振幅达6.0 kV,线路C相电压振幅仅有 0.6 kV;线路 B,C 相相角的振幅为 0.50°~0.60°,A 相相角的振幅为 0.20°~0.25°,二者相差不大。
(3)电压幅值振荡频率集中在0.3~1.5 Hz,以1.47 Hz为主。
(4)有功功率波动幅值及占比较小。有功功率波动不明显,基本在10 MW以内。
(5)线路有功功率、无功功率、电压振荡均为等幅振荡。对阳东I线正序电压、有功功率、无功功率、A相电压、B相电压、C相电压进行Prony分析表明:阳东I线上述6个量的振荡均为零阻尼等幅振荡或负阻尼。
1.4 线路电压谐波分量统计
对现场PMU进行检查并利用标准源进行检测,在使用50 Hz标准源的情况下,没有出现电压幅值波动情况。为了客观分析,采用CAAP 2008跨平台电力故障录波分析软件对现场故障录波器手动触发录取的暂态波形进行谐波分析(故障录波器最初数据采样率为10000点/s)。可以得出,阳东I线的A,B,C三相电压谐波分量之间的差别主要是:
(1)A相47次谐波含有率较低,仅为0.01%,49次谐波含有率达到0.49%;
(2)B相47次谐波含有率达0.31%,49次谐波含有率为0.26%;
(3)C相47次谐波含有率为0.04%,49次谐波含有率为0.03%;
(4)A,B相相对于C相来说,49次谐波及其周边的频谱含有率明显较高。
阳东II线、阳东III线的三相电压与阳东I线的三相电压在谐波含有率方面具有一样的规律。
2 理论推导与仿真分析
2.1 频率混叠和采样定理
采样定理又称抽样定理,是由Nyquist和Shannon C.E.分别于1928年和1949年提出来的,所以又称Nyquist抽样定理或Shannon抽样定理。在对连续信号作抽样时,首先要了解信号的最高截止频率fc,以确定应选取的抽样频率fs。当信号不是有限带宽时,在抽样前应对信号做模拟滤波,滤掉大于fc的高频成分。抽样频率fs又称“Nyquist频率”,使频谱不发生混叠的最小抽样频率fsmin=2fc。
模拟信号经过A/D变换转换为数字信号的过程称之为采样,信号采样后其频谱产生了周期延拓,每隔1个采样频率重复出现1次。当采样频率小于最小抽样频率时,就会发生频混现象,又称为频谱混叠效应,它是由于采样信号频谱发生变化,高、低频成分混淆的一种现象,会导致在信号复原时丢失原始信号中的部分信息。图2为发生频混现象的时域信号波形。图2a为采样频率正确的情况,以及其复原信号;图2b为采样频率过低的情况,复原的是一个虚假的低频信号。
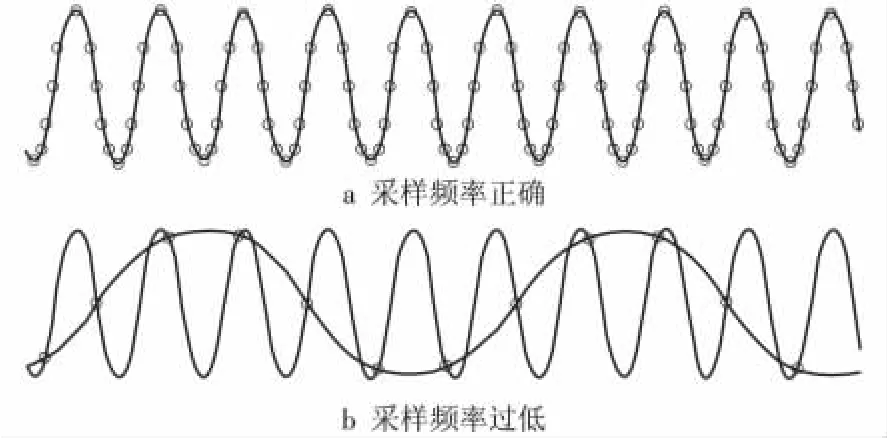
图2 发生频混现象的时域信号波形
2.2 PMU算法基本原理
PMU与常规测控装置的最大区别为:它以GPS秒脉冲作为采样基准进行等间隔的采样,对采样获取的离散采样点进行相应的数学变换,从而获取相应的相量信息,除了和常规测控装置一样的幅值信息外,还包括绝对角度信息。目前大部分PMU厂家以离散傅立叶变换(DFT)作为算法基础。
输入信号采样序列为
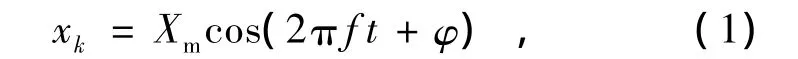
式中:Xm为幅值;φ为相角;f为频率;t为时间。
DFT公式为
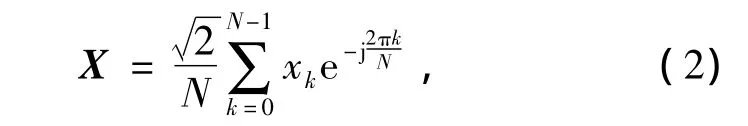
式中:X为所求相量;N为1个周波内的采样点数。对连续采样序列xk取一定长度的数据窗进行DFT求得相量。
电力系统实际运行中,20次以上的谐波含量通常都极低。DL/T 280—2012《电力系统同步相量测量装置通用技术条件》中规定:叠加20%的13次及以下的谐波电压,基波电压幅值和相位测量误差改变量应不大于100%。对13次以上的谐波影响未做要求。
PMU算法为了减少计算量,降低采集单元的CPU负荷,虽然暂态录波部分采用4800点/s的数据采样率,但实际内部采用的是每2点抽1点的方法,即采用2400点/s的采样率进行计算。正常情况下,采样率4800点/s和2400点/s的测量精度差异极小。
根据采样定理,PMU也应该设计一个抗混叠的低通滤波电路,但由于PMU对相位精度的要求极高,如果低通滤波电路的截止频率设计得较低,相应的滤波电容值需选取得较大,当长期运行及老化等原因导致电容值发生变化时,会对相位测量精度产生影响。PMU A/D采样的前置滤波电路的滤波截止频率选得比较高,为1 MHz,当以2400点/s的采样率工作时,如果A/D采样中混有24次以上的谐波分量,会在相量计算中引入1个低频信号,导致相量计算失真。
2.3 高次谐波信号对相量影响的理论仿真
根据PMU算法原理,假定真实信号为一个标准的50 Hz正弦信号,在该正弦信号上叠加0.5%的高次谐波噪声。利用 Matlab仿真[3]发现:在叠加47次和49次谐波分量时,以2400点/s和4800点/s 2种不同的采样率进行计算带来的误差比较明显,分别如图3和图4所示。
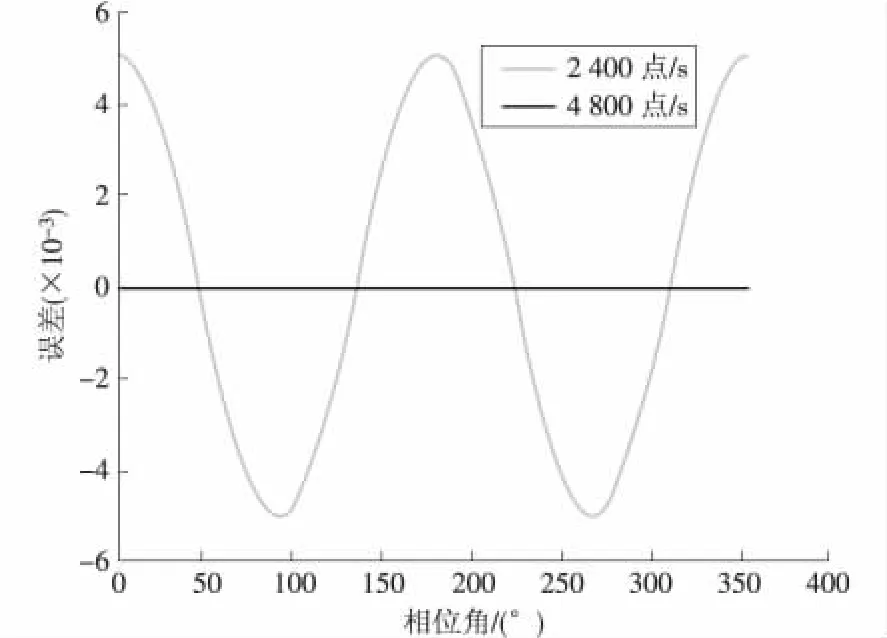
图3 47次0.5%谐波含有率采样误差对比
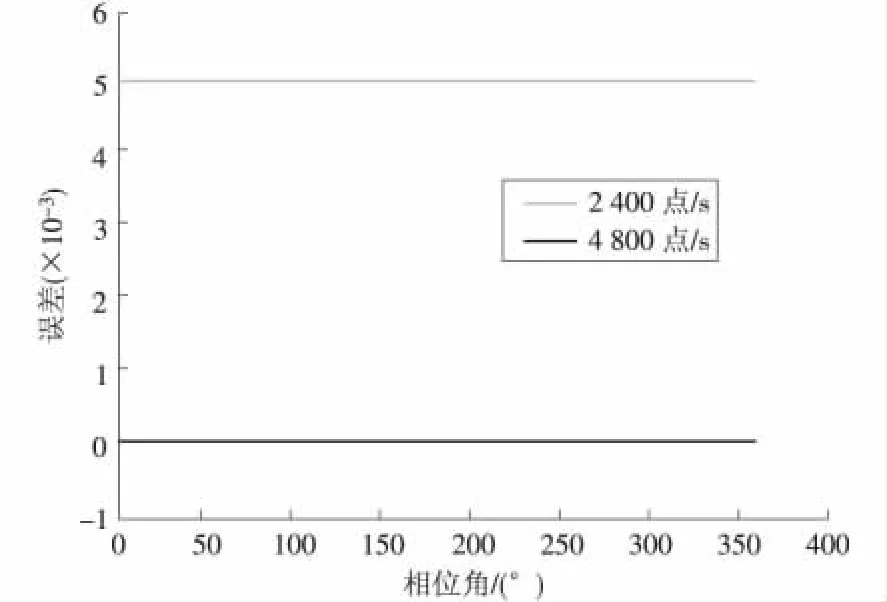
图4 49次0.5%谐波含有率采样误差对比
而在叠加其他高整次谐波分量时,2种不同的采样率下,相量幅值计算的误差都比较小,如图5所示。通过仿真可以看出:49次以上的高次谐波对PMU的测量精度影响很小。
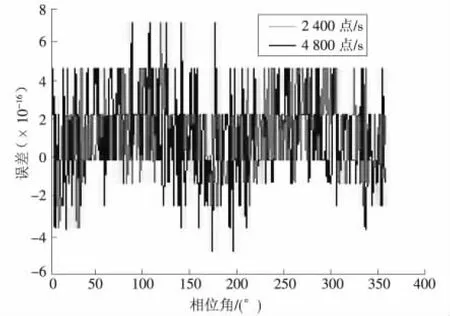
图5 49次以上高整次0.5%谐波含有率采样误差对比
2.4 异常波动仿真再现
根据理论仿真可知,47~49次整次谐波以及45~49次非整次谐波都会对以2400点/s采样率的PMU幅值测量带来误差。在实验室内以继电保护测试仪和信号发生器作为测试设备,在PMU的交流电压A通道上加入叠加了0.5%谐波分量的电压信号,通过动态文件查看A相通道幅值测量精度变化情况。
在57 V基波电压上叠加了0.276 V的47次谐波时,其对应的PMU形成的动态数据文件如图6所示。从图中可以明显看到:在2400点/s采样率下,叠加了47次谐波的A相电压幅值有异常摆动,摆动幅度达到2.7 kV,而无谐波叠加的B相电压动态数据非常平稳。

图6 叠加47次谐波的和无谐波的PMU暂态波形对比
3 软件升级前、后线路电压对比
从PMU电压幅值的摆动情况以及现场故障录波器的录波数据可以看出,谐波含量是时变和不确定的,但从定性和趋势方面来说A,B两相电压的47次谐波、49次谐波(尤其是49次谐波)含量明显高于C相电压。对阳城电厂PMU内部程序进行升级,即应用4800点/s采样率进行PMU的计算。从实际运行情况看,线路电压幅值一直处于合理范围内。软件升级前、后电压波形如图7、图8所示。
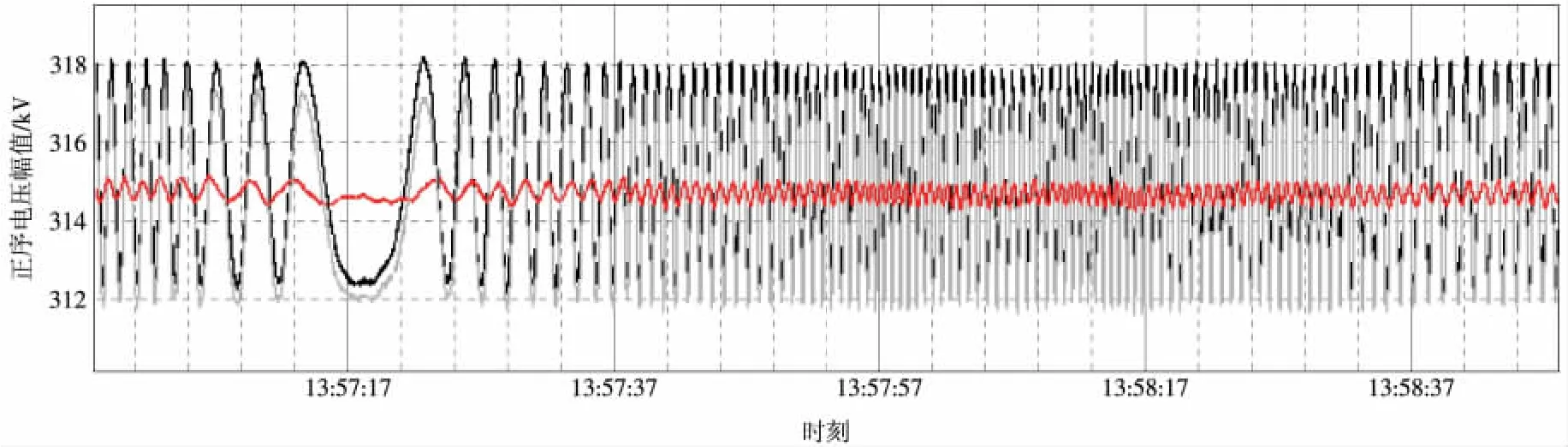
图7 软件升级前PMU展示的电压波形
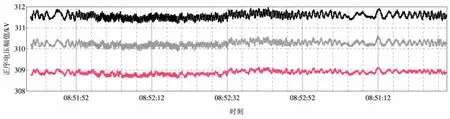
图8 软件升级后PMU展示的电压波形
4 结束语
本文从理论仿真和装置实际应用方面证实了47次、49次谐波分量在2400点/s采样率下对PMU电压幅值测量精度的影响。将分析成果应用于阳城电厂发输电系统,消除了线路电压幅值异常波动的问题,可为实际电力系统运行与监视、PMU电压曲线异常波动分析等提供参考。
[1]刘振亚.特高压电网[M].北京:中国经济出版社,2005:114-116.
[2]Phadke AG.Synchronized phasor measurements in power systems[J].IEEE Computer Applications in Power,1993,6(2):10-15.
[3]张森.MATLAB 6.0程序设计与实例应用[M].北京:中国铁道出版社,2001:50-55.
