房地产业生产效率及技术进步研究

杨茜淋

（北京大学 光华管理学院，北京 100084）

1 房地产业生产函数及全要素生产率的估计

全要素生产率（TFP）是指产出中投入要素解释不了的那部分产出。TFP的水平是由生产中投入要素如何被有效地、集约地利用来决定的。测算全要素生产率的传统方法是索洛余值法，其关键假设是所有生产者都能实现最优的生产效率，从而产出的增长扣除要素投入增长之外的增长都是来自于技术进步。索洛余值是参数法估计的一种，需要设定生产函数的形式，优点是比较直观的阐明了全要素生产率的意义。索洛余值被定义为GY-α∗GK-(1-α)∗GL，其中 GY表示总产出的增长率，GK表示总资本存量的增长率，GL表示总劳动投入的增长率，α表示资本的产出弹性，（1-α）表示劳动的产出弹性。利用索罗余值方法估计房地产业全要素生产率的生产函数模型为柯布道格拉斯生产函数：Yit=Ait，其中，i表示地区，t表示时间。Yit表示产出，Kit表示固定资本存量，Lit表示就业，α表示资本的产出弹性，β表示劳动的产出弹性。

本文估计房地产业生产函数及全要素生产率是基于2002～2011年房地产业24个省、自治区和直辖市的增加值、固定资产投资及就业的面板数据。而固定资本存量数据是通过永续盘存法计算得到的。用永续盘存法来计算固定资本存量就是用基年的固定资本存量减去折旧加上当年的固定资产投资。用公式表示如下：

其中，K代表资本存量，I代表固定资产投资，δ代表折旧率，t代表时间。

2002年房地产的固定资本存量为27561.72亿元，同年增加值为5377.61亿元，固定资本存量约为增加值的5.12倍，所以我们确定各个地区基期固定资本存量数据的方法是用当年房地产增加值乘以5.12来得到固定资本存量，这里，我们需要假设各个地区固定资本存量与增加值的比等于全社会房地产业固定资本存量与增加值的比。

1.1 面板数据单位根检验

面板数据模型进行回归分析之前，需要对数据进行单位根检验，这是避免出现伪回归的前提条件。面板数据的平稳性检验方法与时间序列的平稳性检验是不同的。近年来研究较为成熟的检验方法主要有LLC检验、Breitung检验、Hadrid检验，IPS检验，Fisher-ADF检验。其中LLC检验，Breitung检验、IPS检验的原假设是含有单位根；Hadrid检验的原假设为不含单位根。这里我们选择多种检验方法来进行面板数据的平稳性检验。如果不存在单位根，则数据是平稳的，不会产生伪回归问题；如果存在单位根，还要继续检验是否是同阶单整，如果同阶单整并且存在协整关系，也可以进行回归，不会产生伪回归问题。单位根检验结果见表1。

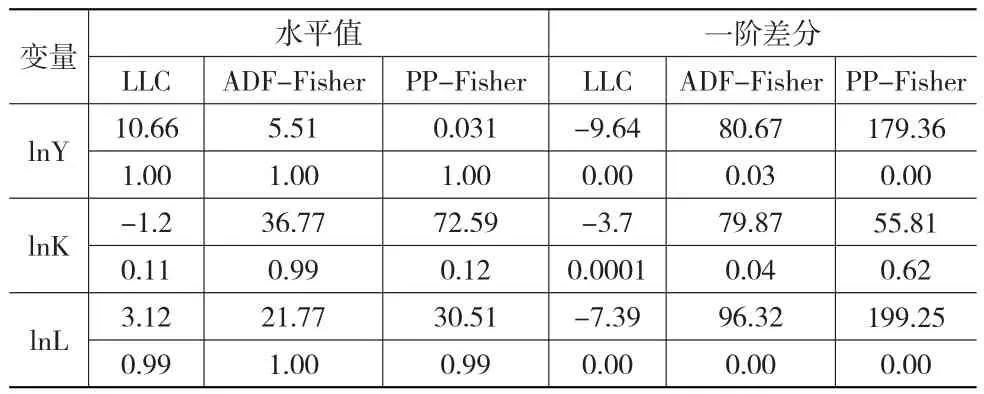
表1 房地产业面板数据单位根检验结果

单位根的检验结果表明，lnY、lnK和lnL在5%显著性水平下为非平稳序列，存在单位根，但是三者都为一阶差分平稳序列，即为一阶单整序列，符合面板协整检验的前提。

1.2 面板数据协整检验

本文主要应用Pedroni构造的7个检验面板变量协整关系的统计量，即4个用联合组内维度描述的Panel v、Panel rho、Panel PP和PanelADF统计量和3个组间维度描述的Group rho、Group PP和Group ADF以及Kao统计量来判断变量间是否存在协整关系。检验结果如表2所示。

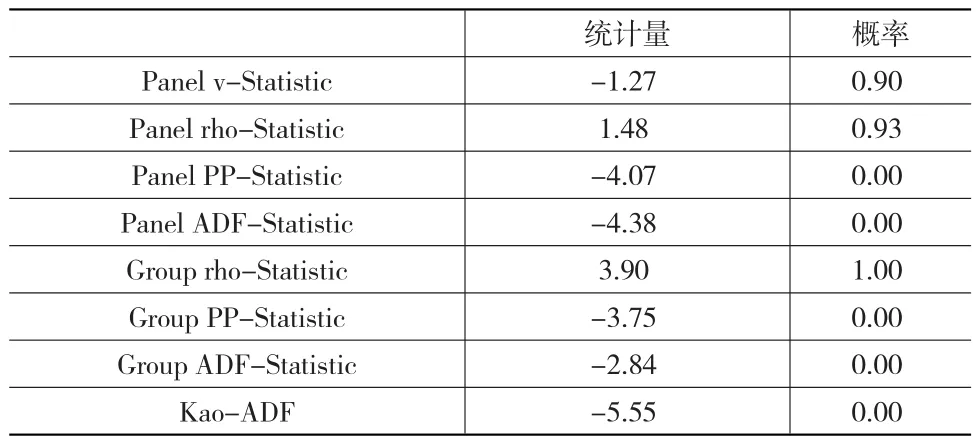
表2 协整检验结果

从表中可以看出，Panel PP-Statistic、Panel ADF-Statisti、Group PP-Statistic、Group ADF-Statistic 和Kao-ADF都拒绝不存在协整关系的原假设，即lnY、lnK和lnL存在协整关系，可以进行回归，不会造成伪回归的后果。

1.3 面板数据模型的选择

面板数据模型的选择通常有三种形式：一种是混合估计模型。如果从时间上看，不同个体之间不存在显著性差异；从截面上看，不同截面之间也不存在显著性差异，那么就可以直接把面板数据混合在一起用普通最小二乘法（OLS）估计参数。一种是固定效应模型。如果对于不同的截面或不同的时间序列，模型的截距不同，则可以采用在模型中添加虚拟变量的方法估计回归参数。一种是随机效应模型。如果固定效应模型中的截距项包括了截面随机误差项和时间随机误差项的平均效应，并且这两个随机误差项都服从正态分布，则固定效应模型就变成了随机效应模型。

在面板数据模型形式的选择方法上，我们经常采用F检验决定选用混合模型还是固定效应模型，然后用Hausman检验确定应该建立随机效应模型还是固定效应模型。

在回归的时候，权数可以选择按截面加权的方式，对于横截面个数大于时序个数的情况更应如此，表示允许不同的截面存在异方差现象。估计方法采用PCSE（Panel Corrected Standard Errors，面板校正标准误）方法。Beck和Katz(1995)引入的PCSE估计方法是面板数据模型估计方法的一个创新，可以有效的处理复杂的面板误差结构，如同步相关，异方差，序列相关等，在样本量不够大时尤为有用。

通过检验，房地产业面板数据适合固定效应模型，估计结果为：

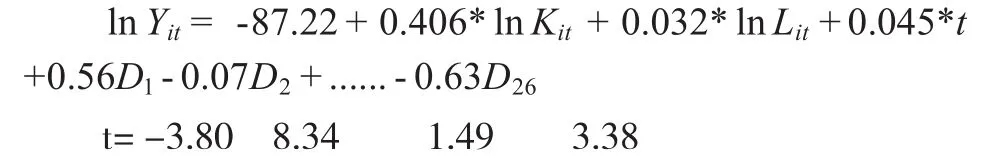
其中，虚拟变量D1,D2,....,D26定义为：

虚拟变量的回归系数结果说明，东部地区的房地产业在基期的全要素生产率的水平较高，中部地区次之，而西部地区的虚拟变量回归系数都比较小，这说明西部地区房地产业在基期的全要素生产率水平较东、中部地区都低。从生产函数的变量系数回归结果可以看出，资本的产出弹性为0.4，而劳动的产出弹性只为0.032，劳动的产出弹性如此之小，是在其他行业回归中从未见过的。相比劳动，资本在房地产业起到了更大的作用。资本存量增加1%，产出就会增加0.4%。

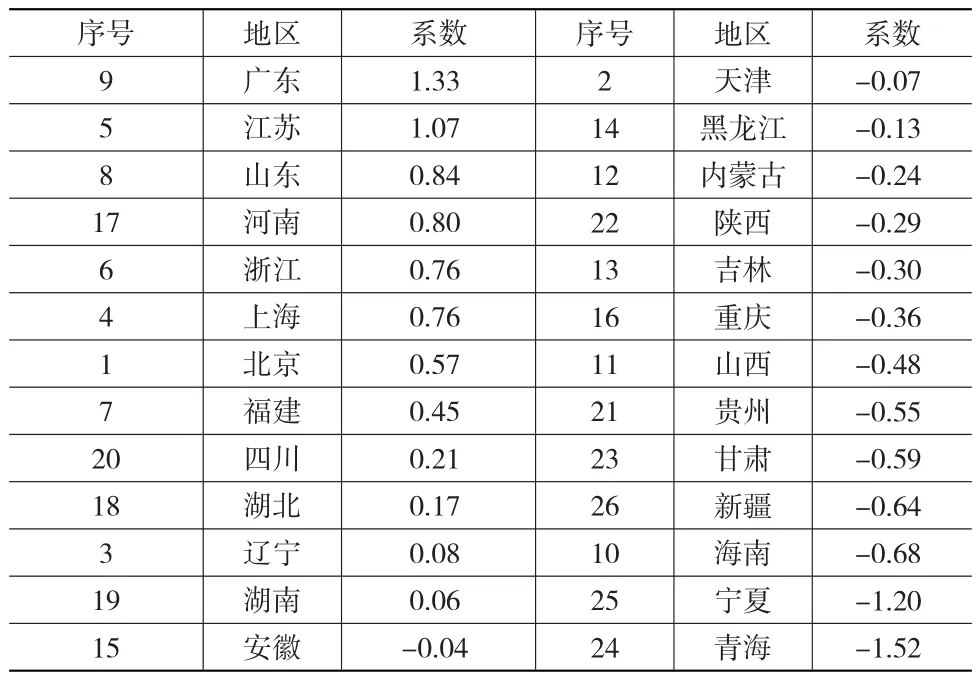
表3 虚拟变量估计结果

2 数据包络分析法（DEA）对房地产业生产效率及技术进步的估计

估计生产效率的方法主要分为两种，一种是数据包络分析法，该方法属于非参数方法，不需要给出具体的生产函数，并且允许多投入和多产出，一般使用软件DEAP 2.1来进行分析。DEA方法的特点是将有效的生产单位连接起来，用分段超平面的组合也就是生产前沿面来紧紧包络全部观测点，是一种确定性前沿方法，没有考虑随机因素对生产率和效率的影响。另一种是随机前沿分析法，该方法属于参数分析方法，即需要先给出生产函数，再来估计该生产函数模型下的技术效率，一般使用软件Frontier 4.1来进行分析，随机前沿生产函数在确定性生产函数的基础上提出了具有复合扰动项的随机边界模型，主要思想是假设随机扰动项由随机误差项和技术损失误差项组成。DEA方法和SFA方法的具体特点及利弊，李双杰等已给出详尽的说明。利用DEA估计我国各地区房地产业的全要素生产率结果与索洛余值方法估计的各地区房地产业的全要素生产率如图1所示。

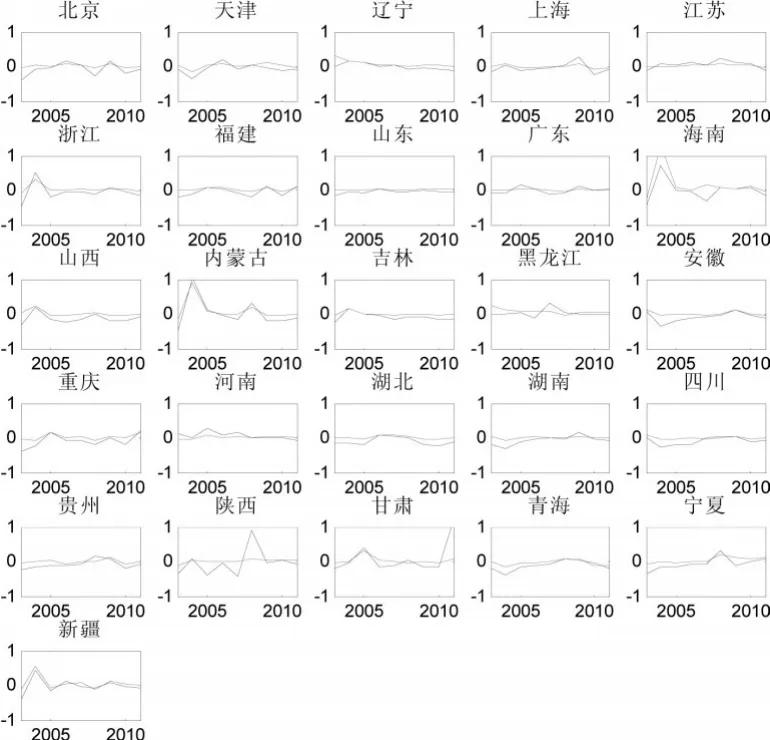
图1 索罗余值法与DEA方法估计的TFP在增长率趋势图

图1绿色曲线表示索洛余值方法估计的结果，蓝色曲线表示DEA方法估计的结果。结果表明，两种方法估计的各地区房地产业全要素生产率基本上具有相同的变化趋势。

图2显示了全要素生产率及其两个组成部分，生产效率与技术进步在各个地区之间的变化趋势，各个地区之间的技术进步变化率的差异并不大，而生产效率在各个地区之间的差异较大，这就导致各地区TFP的不同。各个地区的技术进步基本在1附近，即各个地区技术进步年平均增长率差别不大，而表示各个地区生产效率的曲线波动幅度相对较大且基本为负，说明各地的房地产业的生产效率出现下降的趋势。

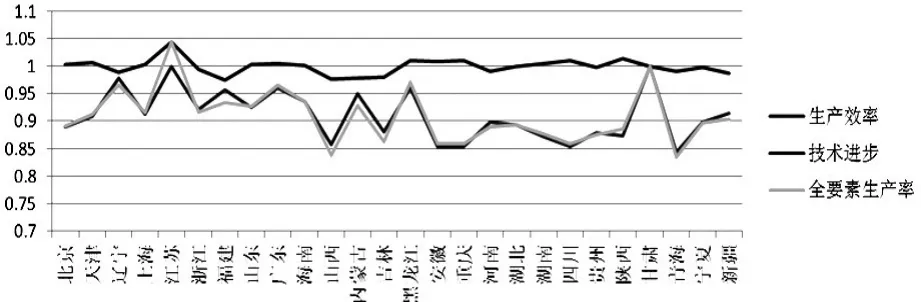
图2 各地区房地产业全要素生产率及生产效率、技术进步年平均增长情况

纵向看，从2003～2011年，房地产业历年生产效率一直下降，而技术进步只有2009年与2011年为负增长，其他年份都为正增长，所以技术进步总体呈现上升趋势。

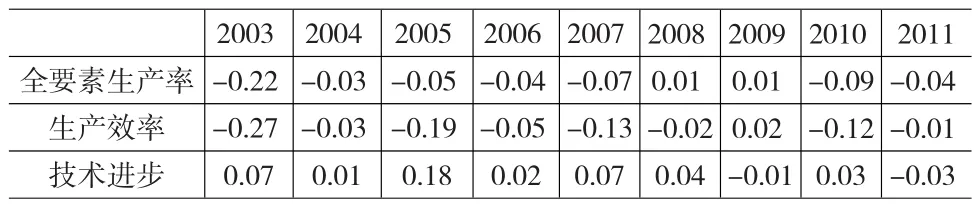
表4 历年房地产业TFP及生产效率、技术进步

3 随机前沿理论及估计结果

3.1 随机前沿理论

首先，我们用图3来说明全要素生产率、技术进步和生产效率之间的关系，以一种要素投入的生产函数为例，曲线1和曲线2分别表示不同技术水平下的生产前沿，所谓生产前沿，是指一定的要素投入量与这种要素投入量能达到的最大产出二者形成的轨迹。当技术进步发生时，生产前沿面就会出现变化，以图3为例，前沿面就是从曲线1变为曲线2。然而现实经济中的生产很少会发生在前沿面上，比如当生产前沿为曲线1时，B点和C点都位于前沿面上，说明技术效率达到最高，为1。而A点位于前沿面一下，即存在技术效率要比1小，即相同要素投入情况下，A点的产出要小于其对应的前沿面上的产出。所以，衡量生产效率，就要看实际产出与潜在产出之间的距离，距离越大，技术效率越低，距离越小，技术效率越高。而全要素生产率的变化，是指图中从原点出发的射线斜率的变化。所以全要素生产率的变化是技术进步和生产效率共同作用的结果。

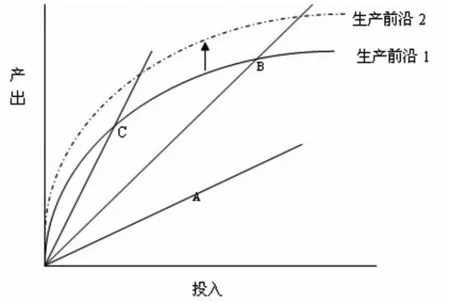
图3 技术进步、生产效率与全要素生产率

测算全要素生产率的传统方法是索洛余值法，其关键假设是所有生产者都能实现最优的生产效率，从而产出的增长扣除要素投入增长之外的增长都是来自于技术进步。索洛余值法把全要素生产率的变化全部归因于技术进步，而忽略了技术效率的作用。然而在现实经济中，大部分生产者并不能达到最优的生产效率，即投入—产出关系的技术边界（Farrell,1957）。所以研究技术效率变的更为重要，基于这种情况，Aigner和Chu(1968)提出了前沿生产函数模型，由于考虑到生产活动中存在随机现象，Aigner,ovell,Schmidt(ALS)和 Meeusen,van den Broeck(MB)同时于1977年提出了随机前沿生产函数。利用对随机前沿生产函数的估计，我们可以通过要素投入数据和产出数据的回归，得到技术效率变化的情况。以下介绍了随机前沿生产函数的具体形式：

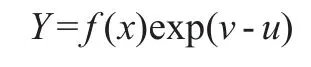
其中v代表影响生产活动的随机因素，一般假设它是独立同分布的正态随机变量，具有零均值和同方差；Y=f(X)exp代表随机前沿生产函数；u代表生产效率，一般假设它为独立同分布的半正态随机变量或指数随机变量，独立于v。

假设生产函数形式为柯布道格拉斯生产函数：

lnY=β0+∑nβnlnXn+v-u其中，Xn代表投入要素

进而技术效率表示为TE=exp(-u)。

本文选取的生产函数为超越对数生产函数，超越对数生产函数是一种包容性很强的变弹性生产函数，它能够很好的反映生产函数中各种要素投入的相互影响及各种投入技术进步的差异等。本文的要素投入包括资本和劳动，其超越对数生产函数的具体形式为：

lnYt=β0+β1lnKt+β2lnLt+β3lnKtlnLt+β4（lnKt）2+β5(lnLt)2+β6tlnLt+β7tlnKt+β8t+β9t2+νt+ut

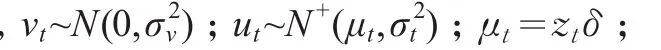
3.2 实证结果

根据随机前沿理论，利用超越对数生产函数，对房地产业进行生产函数及无效率项的回归，回归过程中，由于lnK*lnL与t*lnL项的系数显著为0，所以在生产函数中去除这两项。回归结果如表5所示。

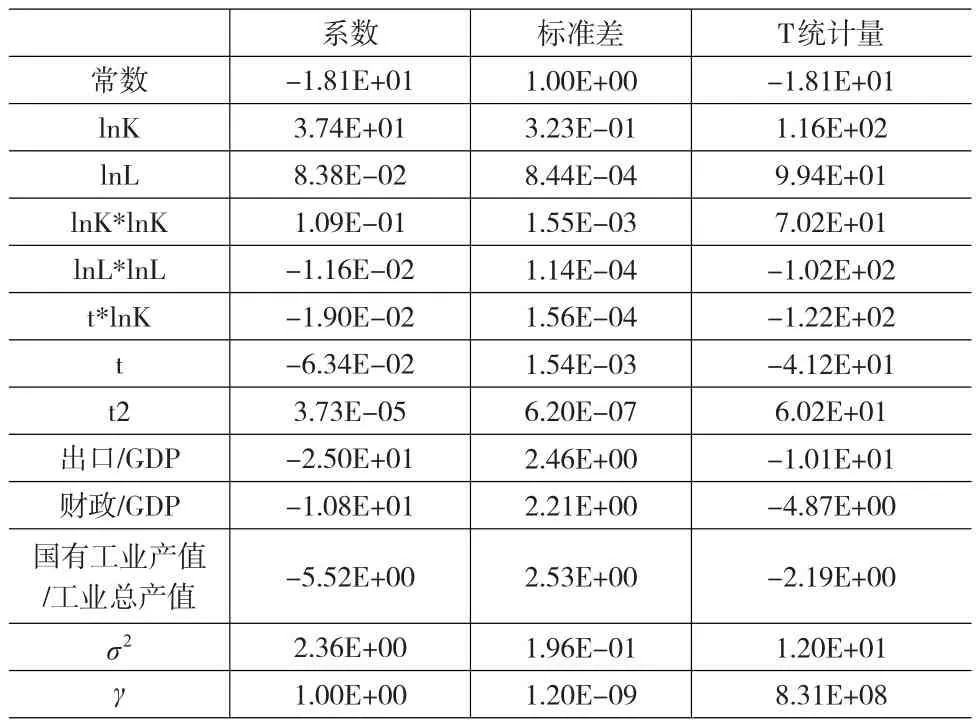
表5 SFA估计结果

利用随机前沿理论估计房地产业的超越对数生产函数的系数回归结果表明，各项变量显著不为零。且γ几乎为1，说明生产的无效率都是有生产无效率引起的，与随机因素几乎没有关系。无效率方程的回归系数表明，国家的开放程度、政府行为及国有化程度对房地产业的生产效率具有促进作用。

3.3 各地区房地产业生产效率趋势

通过SFA方法，我们估计出了各个地区的房地产业2002年至2011年的生产效率变化趋势，把各个地区按照我国东、中、西部来划分，得到图4。

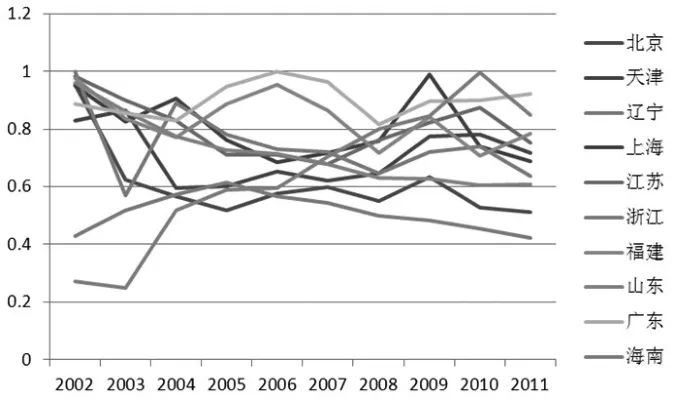
图4 东部地区房地产业生产效率趋势图

东部地区，房地产业生产效率逐年攀升的只有海南省；广东省、福建省和辽宁省的生产效率呈现先上升后下降的趋势，山东省和浙江省的生产效率整体上呈现持续下降的趋势。

除内蒙古、湖北省和黑龙江省以外的其他中部地区房地产业生产效率总体呈现持续下降的趋势。

图5 中部地区房地产业生产效率趋势图

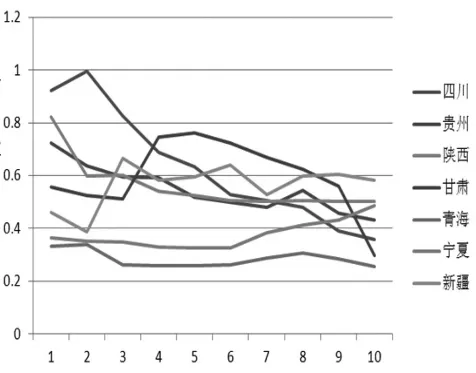
图6 中部地区房地产业生产效率趋势图

宁夏与青海的房地产年平均生产效率最低，宁夏房地产生产效率有上升的趋势，青海房地产生产效率几乎维持不变。西部各地区房地产业的生产效率存在趋同的态势，生产效率较低的地区生产效率有所增长，生产效率较高的地区生产效率有所下降，到2011年，西部各个地区房地产生产效率都落在了0.2～0.6的区间内。

通过对面板数据的回归研究，发现我国房地产业总体生产效率出现下滑趋势，而技术进步是增长的。在生产效率与技术进步共同的作用下，我国从2003～2011年，房地产业的全要素生产率只有2008～2009年是正增长，其余年份都为负增长。研究还发现，中部地区房地产业年平均生产效率的下降要比东部和西部地区房地产业的年平均生产效率下降幅度大。房地产业高的固定资产投入带来了高的产出回报，但并未带来生产效率的提高。而依靠资产投入拉动的房地产业的发展必然是有限的，为了保障房地产业能够在未来持续健康发展，我们需要从提高生产效率上入手，通过提高房地产业的生产效率与技术进步来提高房地产业的全要素生产率。

[1]李双杰，范超.随机前沿分析与数据包络分析方法的评析与比较[J].统计与决策，2009，（7）.

[2]王志刚，龚六堂，陈玉宇.地区间生产效率与全要素生产率增长率分解（1978～2003）[J].中国社会科学，2006,（2）.

[3]张军，章元.对中国资本存量K的再估计[J].经济研究,2003,（7）.

[4]贺菊煌.我国资产的估计[J].数量经济技术经济研究，1992,（8）.

[5]何枫，陈荣，何林.我国资本存量的估计及其相关分析[J].经济学家，2003,（5）.

[6]吴方卫.我国农业资本存量的估计[J].农业技术经济，1999,（6）.

[7]王志刚，龚六堂，陈玉宇.地区间生产效率与全要素生产率增长率分解（1978～2003）[J].中国社会科学，2006,（2）.

[8]葛新元，陈清华，袁强，方福康.中国经济6部门资本产出比分析[J].北京师范大学学报，2000,（4）.

[9]张军，吴桂英，张吉鹏.中国省际物质资本存量估计：1952～2000[J].经济研究，2004,（10）.