我国26个省(区)农村信用社支农效率评价实证研究

仲 深 高 巍 田 立

(哈尔滨商业大学金融学院，黑龙江哈尔滨150028)

一、引言

农村信用合作社是由中国人民银行批准设立、由社员入股组成、实行民主管理、主要为社员提供金融服务的农村合作金融机构。农村信用社为我国农村经济发展提供了重要的金融支持。在发挥重要支农作用的同时，农村信用社也暴露出其自身存在的一些问题，如历史债务包袱沉重、产权不清、经营管理不善、内部人控制现象严重和监督管理体制不合理等。2012年中央发布《关于加快推进农业科技创新持续增强农产品供给保障能力的若干意见》中明确提出“健全地区金融机构考核评价办法”和“深化农村信用社改革”的要求。由此可以看出，对农村信用社支农效率的研究非常必要。基于此，在构建我国农村信用社支农效率评价的网络DEA模型的基础上，运用相关数据，对我国26个省(区)农村信用社支农效率情况进行测度，期望对我国农村信用社的发展提供一定的理论支持。

二、网络DEA模型

1978年Charnes，Cooper和Rhodes提出数据包络分析(Date Envelope Analysis，DEA)模型，用于测度多投入、多产出的系统效率。随着对复杂系统实践研究的不断深入，传统DEA方法考虑从投入到产出的中间过程和数据，从“黑箱”中直接得出效率值已经无法满足管理与政策发展的需要。在此背景下，网络DEA(Network DEA)得到了快速发展。网络DEA模型是指整个评价体系由包含两个或两个以上的子系统构成，子系统间由中间变量进行链接的多投入、多产出的系统效率评价模型。

如果将农村信用社支农看作一个系统，可以将这个系统分为两个子系统，第一个子系统是农村信用社自身运营阶段，可以通过投入资本和劳动力进行经营，产出可以看作是存款和贷款;第二个子系统是农村信用社利用资金支持“三农”的阶段，投入变量是贷款和额外投入的土地资源，产出变量则是农业产值和农民收入。由此得出农村信用社支农效率网络DEA评价模型流程示意图，见图1。

图1 农村信用社支农效率网络DEA评价模型流程

下面具体给出投入型网络DEA效率模型的CRS(规模报酬不变)和VRS(规模报酬可变)线性结构(具体内容可见Holod和Lewis(2011)的论述)。其中，I表示投入变量，O表示产出变量，Z表示中间变量，ε和k分别代表支农相对效率和近似反效率。

1.投入型网络DEA的CRS结构

2.投入型网络DEA的VRS结构

三、我国农村信用社效率测定及分析

1.指标选择和数据来源

通过上述构建模型，可以选择相应的指标变量，其中初始投入指标包括地区每万人营业网点数和地区每万人从业人员数，代表前期的资本和劳动力投入;中间指标包括存款总额和贷款总额，其中贷款总额还要作为第二阶段的投入，另外，将地区土地面积作为新中间投入变量;最终产出变量则包括农村人均收入和第一产业总产值。

由于北京、天津、上海、重庆没有农村信用社机构，西藏地区相关数据缺失，故排除以上5个地区。所用指标数据来源于中国银行业监督管理委员会公布的《中国银行业农村金融服务分布图集》和《2012年中国县(市)社会经济统计年鉴》。变量指标的统计性描述见表1。

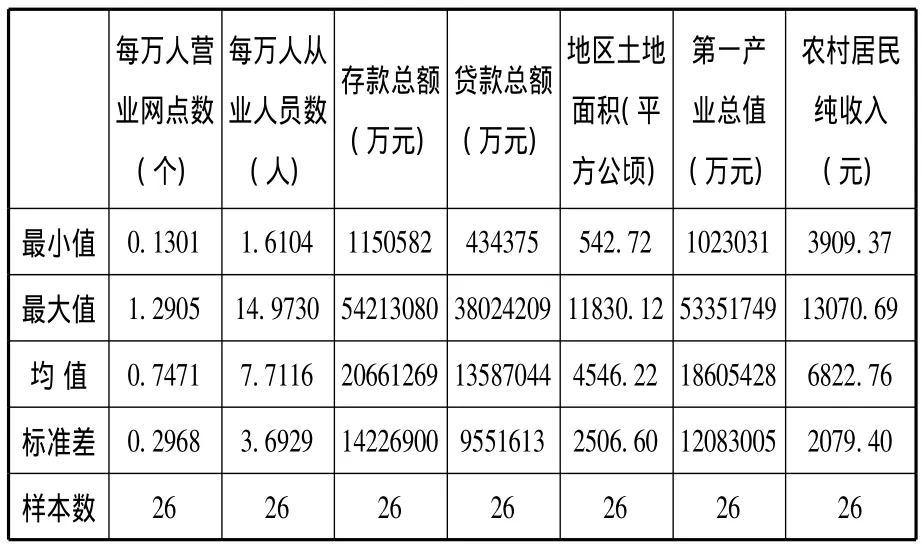
表1 各变量指标的统计性描述

2.实证分析

根据上述构建的我国地区农村信用社支农效率评价网络DEA模型，选择每万人营业网点数和每万人从业人员数为投入指标，存款总额和贷款总额为中间变量，各地区耕地面积为中间投入变量，农村居民纯收入和第一产业总产值为产出变量，运用MaxDEA 6.3软件进行求解，具体结果见表2。

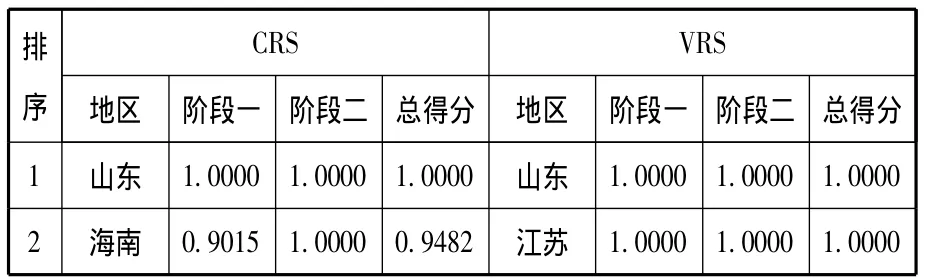
表2 我国26个省(区)农村信用社支农效率评价结果

3 江苏 0.8983 1.0000 0.9464 海南 1.0000 1.0000 1.0000 4 浙江 0.8326 1.0000 0.9087 湖南 1.0000 1.0000 1.0000 5 河南 0.8294 0.8436 0.8364 浙江 0.8963 1.0000 0.9453 6 河北 0.8701 0.6335 0.7332 河南 0.8435 0.8633 0.8533 7 广东 0.7786 0.6546 0.7113 广东 0.8310 0.8275 0.8294 8 湖南 0.5256 0.9519 0.6772 河北 1.0000 0.6437 0.8025 9 安徽 0.6669 0.5145 0.5808 安徽 0.7482 0.5275 0.6271 10 辽宁 0.4474 0.6049 0.5144 福建 0.4097 0.7723 0.5354 11 福建 0.4421 0.6083 0.5120 广西 0.8278 0.3295 0.5308 12 广西 0.7792 0.3038 0.4372 江西 0.5169 0.5080 0.5129 13 湖北 0.4072 0.4673 0.4352 辽宁 0.3473 0.8820 0.5098 14 江西 0.5138 0.3539 0.4191 山西 0.4023 0.5936 0.4927 15 山西 0.9509 0.2529 0.3995 湖北 0.4253 0.5068 0.4558 16 陕西 0.4567 0.2580 0.3297 陕西 0.5531 0.2959 0.4136 17 吉林 0.1621 0.7541 0.2668 云南 0.8546 0.1514 0.4019 18 贵州 0.3677 0.1968 0.2564 四川 0.6989 0.0253 0.3738 19 宁夏 0.1310 1.0000 0.2316 贵州 0.3334 0.3517 0.3414 20 云南 0.8304 0.1247 0.2233 吉林 0.1980 0.6672 0.2879 21 四川 0.6957 0.0214 0.1675 宁夏 0.1540 0.7813 0.2573 22 黑龙江 0.1463 0.1629 0.1542 黑龙江 0.2108 0.2805 0.2269 23 新疆 0.2536 0.0694 0.1090 甘肃 0.2994 0.1082 0.2136 24 甘肃 0.2928 0.0641 0.1052 新疆 0.2661 0.0604 0.2058 25 内蒙古 0.1376 0.0491 0.0724 内蒙古 0.1841 0.0933 0.1606 26 青海 0.0275 0.0521 0.0360 青海 0.0278 0.0483 0.0290

从实证结果来看，VRS条件下的得分比CRS的得分总体要高出少许，但整体排序和结果没有明显变化，由此可以证明两个模型结果的有效性。

在CRS(规模报酬不变)条件下，农村信用社自身运营阶段的效率平均值为0.5517，其中，排在前三位的是山东、山西、河南，得分分别为 1、0.9509、0.9015;排在最后三位的是青海、宁夏、内蒙古，得分分别为 0.0275、0.1310、0.1379。农村信用社贷款支农阶段的效率平均值为0.4978，其中，山东、河南、江苏、浙江、宁夏的效率值均为1;排在最后三位的是四川、内蒙古、青海，得分分别为0.0214、0.0491、0.0521，得分不足0.1的有5个地区，两极分化比较严重。农村信用社支农效率总得分平均值为0.4620，其中，排名前三位的是山东、河南、江苏，得分分别为1、0.9482、0.9464;排名最后三位的是青海、内蒙古、甘肃，得分分别为 0.0360、0.0724、0.1052。

在VRS(规模报酬可变)条件下，农村信用社自身运营阶段的效率平均值为0.5780，其中，山东、江苏、海南、湖南、河北的效率值均为1;排名在最后三位的是青海、宁夏、内蒙古，得分分别为 0.0278、0.1540、0.1841。农村信用社贷款支农阶段的效率平均值为0.5507，其中，山东、江苏、海南、湖南、浙江的效率值均为1;排名在最后三位的是四川、青海、新疆，得分分别为0.0253、0.0483、0.0604。农村信用社支农效率得分平均值为0.5387，其中，山东、江苏、海南、湖南的效率值均为1，排在最后三位的是青海、内蒙古、新疆，得分分别为 0.0290、0.1606、0.2058。

四、结论

第一，我国农村信用社自身运营效率相对较高。农村信用社在我国农村覆盖范围极广，被广东农村居民认为是首选的金融机构。再者，我国居民一直都存在过度储蓄的习惯，使得农村信用社吸纳存款和发放贷款业务可以很好的展开。

第二，我国农村信用社发放贷款支农效率相对较低。我国农村信用社发放贷款的效率较高，但是贷款支农的效率较低，这说明贷款资金很可能没有发放到“三农”方面。近些年农村信用社一直面临着诸多问题，其中一个就是控股股东和内部职工滥用权利套取资金的问题，所以，我国农村信用社必须进一步加强监督管理，深化改革。

第三，我国各地区农村信用社支农效率差异极大。通过实证结果可以很容易看出，各省农村信用社支农效率值差异极大，有的省份，如山东，得分非常高，而有的省份得分却极低。不难看出，东部各省效率值整体较高，而西部各省的效率值则整体偏低，这应该与当地经济发展和金融发展水平相匹配。

第四，我国农村信用社支农效率还有比较大的提升空间。随着农村经济和社会的不断发展，对农村金融体系提出了更高的要求。根据测度效率值可以看出，很多地区还具有比较大的提升空间，而这种提升应该以深化农村信用社改革为基石。

［1] 魏权龄.评价相对有效性的数据包络分析模型——DEA和网络DEA［M] .北京：中国人民大学出版社，2012：333 －336.

［2] Holod D.，Lewis H.Resolving the Deposit Dilemma：A New Bank Efficiency Model［J] .Journal of Banking and Finance，2011，35(11)：2801 －2810.