大多普勒条件下伪码快捕技术

梁保卫，涂海洋

(1.中国电子科技集团公司第五十四研究所，河北石家庄 050081;2.空军驻石家庄地区军事代表室，河北石家庄 050081)

0 引言

直接序列扩频以独特的抗干扰、抗截获能力，在移动通信、卫星通信和军事通信等领域得到了广泛的应用。特别是无人机通信领域，上行遥控链路广泛采用直接序列扩频技术体制，当无人机高速飞行时，接收信号中的载波多普勒高达几十kHz，因此大多普勒条件下的长码捕获是目前亟待解决的问题。随着无人机技术的进步，具有较高飞行速度的无人机越来越多地投入使用，给通信系统带来了新的挑战。相对于普通低速无人机，高速无人机具有更高的径向速度和加速度，使得接收信号中的载波多普勒高达几十kHz，为了抗截获的需要，高速无人机通常采用扩频增益高的上行链路;因此高速无人机中大多普勒条件下的长码捕获是目前亟待解决的问题。

伪码的捕获有多种，主要分为串行捕获方法和并行捕获方法［1－3］，串行捕获方法实现简单，捕获速度慢，主要应用于伪码周期短对捕获时间要求不高的情况下;并行捕获方法速度快实现结构复杂，主要应用于低信噪比、大动态及对捕获时间要求高的情况下。在实际中综合捕获性能和硬件实现复杂度，通常采用串并组合的捕获方法，比如基于FFT频域分析的载波并行、伪码串行的捕获方法［4］，基于FFT/IFFT分析的伪码并行、载波串行的捕获方法。这些算法都是采用了串并组合的捕获策略，不管是载波串行捕获还是伪码串行捕获，只要有一方面是串行捕获就不可避免地延长高速无人机的信息获取时间。文章在基于FFT的部分相关伪码捕获算法基础上，提出了一种基于FFT的分段匹配滤波的快捕算法，即利用匹配滤波器的快速相关能力，将伪码并行捕获和载波并行捕获应用在一种算法，以分段匹配滤波器(SMF)代替滑动相关器，FFT频域分析载波频偏，在保证捕获性能的情况下，显著缩短了捕获时间。

1 基于FFT的部分相关快捕算法

基于FFT的部分相关捕获算法是在传统的滑动相关法的基础上结合了FFT频谱分析技术对码相位和载波多普勒组成的二维平面采用载波并行伪码串行的搜索策略。在搜索一个码相位单元同时对整个多普勒变化的范围进行估计，二维的搜索变成在码相位方向的一维搜索，搜索时间仅为无多普勒时采用一维搜索的时间［5，6］。

基于FFT的部分相关捕获原理框图如图1所示，输入信号经过下变频器及低通滤波后进入解扩部分，FFT频偏估计过程如下:本地长度为N的扩频码序列每滑动一次，对一个符合周期内的数据进行部分相关得到D个数据点，利用这D点数据做M(M≥D)点的FFT运算，M是2的整次幂，如果D＜M，用0补齐。滑动N次后，从N次FFT的数据中找到估算出的系统多普勒，并找到PN码相位对准的位置，在实现伪码捕获的同时，将估算出的频偏值补偿给载波环。相关器相关之后，如果未对准，信噪比极低，FFT的输出为噪声;对准之后，系统信噪比提高，从FFT数据中找到最大值的点，实现多普勒的估计。

图1 基于FFT的伪码捕获原理

2 基于FFT的分段匹配滤波快捕算法

2.1 基本原理

改进的基于FFT的分段匹配滤波捕获算法利用SMF的快速相关和FFT的频谱分析能力，对码相位和载波多普勒组成的二维平面采用一种新的搜索策略，该策略在一个码周期内搜索N个伪码相位，并在每个伪码相位内对载波多普勒进行并行搜索，完成整个码相位和载波多普勒的搜索只需N个码周期。

改进的基于FFT的分段匹配滤波捕获原理框图如图2所示。输入信号经过下变频器及低通滤波后进入解扩部分，在这种结构下，本地长度为N的扩频码序列被分成D段，每段长度为P(N=PD)，第1段存储到第1个匹配滤波器，第2段存储到第2个匹配滤波器，以此类推，直到最后一段码序列存储到第D个匹配滤波器。当接收数据依次进入这D个匹配滤波器后，得到D个不同相位的部分相关值，对其D个数据作M点的FFT运算，并判断峰值是否超过门限。若超过门限，说明码相位捕获成功，并根据FFT峰值的位置估算出系统多普勒，将估算出的频偏值补偿给载波环。

图2 基于FFT的分段匹配滤波快捕原理

2.2 SMF参数选取

量化比特数是SMF设计中一个非常重要的参数，量化比特数越高，SMF的性能越好，但硬件代价也越大。在实际中量化比特数总是有限的;文献［7］表明当量化比特数为6时，系统的误码率曲线几乎与模拟相关时的曲线一致;当量化比特数为3时，系统损失＜2 dB。考虑到长码扩频需要的SMF长度较长，避免硬件资源太大，采用5 bit量化方案。

取样间隔是SMF设计中另一个非常重要的参数，取样间隔越多，SMF的性能越好，但需要的SMF的长度越长，硬件代价也越大，特别是在高增益直扩系统中甚至难以实现，设计时必须根据系统要求折中处理。按照采样定理要求，确保信号无失真的最小采样倍数为2倍采样，若每个码元2倍取样后送入SMF电路，SMF在每个PN码周期内将会有2个相关峰输出，使得相关峰变得模糊，导致同步电路性能变差。文献［8］提出在2倍抽样率时，通过在SMF前边增加前端处理电路，可使系统误码率与10倍取样间隔的效果一致，前端处理算法如下:

前端处理算法等效于低通滤波器，使得在2倍采样时2个相关峰变成一个更加尖锐的相关峰，利于信号的捕获和时钟同步。

2.3 性能分析及参数的选取

2.3.1 常规相关器的频响

设相干积分时间T为一个伪码周期，伪码码片宽度为 Tc，N为一个周期内的码片个数，N=T/Tc，fp为本地载波频率与发送频率的频率偏移值。

频率偏移对相干积分后的能量峰值的影响可以用η(fp)表示:

式中，当fpT=1时，η(fp)=0，即相关峰为0，无法实现相关峰捕获;此时，fp=1/T。

2.3.2 基于FFT的分段匹配滤波的频响

设每个SMF的长度为P，则D个分段匹配滤波器的共同累计时间T为一个伪码周期。D个长为P的分段匹配滤波器进行M点FFT运算后的幅值Z(k)为:

频率偏移对FFT第k点的能量峰值的影响可以用 G(fd)［9］表示:

式中，当PfdTc=1时，G1(fd)=0，即相关峰为0，无法实现相关峰捕获;此时，fd=1/PTc=D/NTc=D/T;

因此由式(2)和式(6)的结论可知，基于FFT的分段匹配滤波捕获算法频率搜索范围比传统算法扩大了D倍。

由于FFT存在扇贝损失，FFT估算频率的误差由频率分辨率决定，FFT点数M的确定取决于两个因素，首先必须大于D，其次根据系统需要的频率估计精度来确定M的上限，在FFT处理中，频率分辨率为fs/M，其中fs为采样率，当采样率固定时，增加分析点数M可以提高频率估计精度。但在实际工程中，提高FFT的点数是以增加硬件的复杂度为代价的，如果FFT的点数太大对于机载设备这是不能容忍的;要进一步缩小载波估算频差，以满足载波跟踪环的捕获的要求，这里采用对FFT分析的数据再进行谱线估计用于进一步提高估算精度。

2.4 两谱线比值法

两谱线比值校正法主要利用主瓣峰顶附近两条谱线的窗谱函数的比值，建立一个以校正频率为变量的方程，解出校正频率，再进行幅值和相位修正。谱线比值法中应用最多的是Grandke法，当信号频率不是FFT的频率分辨率的整数倍时，由于FFT的扇贝效应引起频谱泄漏，此时信号的实际频率位于FFT主瓣内2条最大谱线之间，可以利用最大的3根谱线的比值估计信号的实际频率在2条谱线之间的精确位置。设x(t)的M点FFT记为X(m)，并记X(m)幅值最大处的谱线序号为m，与m谱线相邻的两谱线序号记为m－1和m+1，故这3条谱线的复数值记为Xm－1、Xm和Xm+1。

频率校正fr如下:

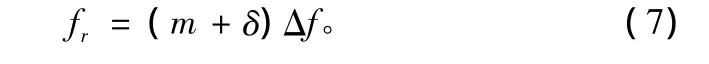
式中，Δf为FFT的频率分辨率;δ为无量纲频率偏移量，简称频偏如下［10］:

3 仿真测试及结果分析

以某直扩系统为例，输入中频为140 MHz，PN码速率为8.192 Mbps，数据速率为4 kbps，信号经中频采样，数字下变频低通滤波后，得到PN码速率的基带信号，经过内插抽取后，送给SMF为2倍采样的信息，PN码为2048位GOLD序列，SMF的总长度为4096位，多普勒频移为±50 kHz。

在伪码载波二维串行法中，设检测为单次驻留，平均捕获时如下［11］:

式中，Pd为检测概率;Pfa为虚警概率;K为虚警因子;m为待搜索的频点数量;q伪码码元数量;τd为单次驻留积分时间决定。

基于FFT的部分相关捕获算法中，检测为单次驻留，平均捕获时间如下:

式中，TN为FFT处理时间。

基于FFT的分段匹配滤波器捕获算法中，检测为单次驻留，平均捕获时间如下:

在虚警概率Pfa=10－3，检测概率Pd=90%时，3种方法的平均捕获时间如表1所示，由表1可知，基于FFT的分段匹配滤波器法比基于FFT的部分相关捕获法捕获时间提高了大约2000倍。

表1 捕获时间对比表

表2为频率分辨率对比表，要满足多普勒频移为±50 kHz的要求，选择分段匹配滤波器的个数D=32，再采用补零法做 M分别为32、64和128点FFT，由表2可知，增加FFT的点数不能满足载波跟踪环几百Hz的捕获带要求，对32点FFT数据进行谱线比值法后频率分辨率提高了一个数量级，通过谱线比值法后估算的频差最大为80 Hz，满足载波跟踪环几百Hz的捕获带要求。

表2 频率分辨率对比表

在实际工程中，对采用该算法的调制解调器进行误码性能测试，误码率曲线如图3所示，从图3可以看出，该算法解扩解调损失 ＜2 dB，满足工程要求。

4 结束语

改进的基于FFT的分段匹配滤波捕获算法可以解决长码和大多普勒条件下高速无人机的快速捕获问题［12］，FFT的频谱分析使得频率搜索可以并行实现，SMF结构使得伪码捕获也可以并行实现，将二者巧妙结合，同时可以实现伪码和大多普勒的并行捕获，捕获时间显著缩短;针对FFT分析存在的扇贝效应，采用谱线比值法对FFT输出数据进行处理，可进一步提高频率分辨率，以满足载波跟踪环的捕获带要求。对此方法的理论分析和工程实测结果表明，该算法捕获时间快，误码性能优良，且工程实现简单，具有较高的理论意义和工程实用价值，可有助于解决大多普勒环境下长码捕获时间长这一关键技术难题。 ■

［1］许 斌，崔 永，王传鑫.基于FFT的高动态直扩信号快捕改进方法研究［J］.理论与方法，2009，28(8):17－20.

［2］王西夺，孙晓峰.一种GPS信号的快速捕获方法［J］.遥感与导航定位，2012，42(3):34 －37.

［3］班华福，王世练，朱 江.大多普勒下基于FFT伪码捕获技术研究［J］.通信技术，2011，44(8):36 －39.

［4］陈 培，王 云，陈 杰，等.短时相关和 FFT相结合的伪码快速捕获算法［J］.电子科技大学学报2009，38(1):59－62.

［5］LIU Yun-fei，CHEN Zhi-jun，GUO Su-li.Implement and Performance Analysis of PN Code Acquisition Based on FFT［C］∥Proceeding of the 5th World Congress on Intelligent Control and Automation Hangzhou，2004.

［6］SPANGENBERG S M，SCOTT L.An FFT-Base Approach for Fast Acquisiton in spread Spectrum Communication Systems［J］.Wireless Personal Communications，2001(13):27－56.

［7］胡捍英，邬江兴，樊昌信，等.1bit量化相关接收DS/CDMA通信方式及性能［J］.西安电子科技大学学报，2002，29(4):439 －443.

［8］曾兴雯，贺彦国，李 栋，等.DS_CDMA多比特量化相关接收性能分析［J］.西安电子科技大学学报，2002，29(4):439－443.

［9］郭素丽，刘云飞.一种基于FFT的伪码快捕方法［J］.无线电通信技术，2003，29(1):11 －13.

［10］柏 林，董鹏飞，六小峰，等.比值法的频率估计精度分析［J］.重庆大学学报，2010，33(11):7 －12.

［11］王西夺，孙晓峰.一种GPS信号的快速捕获方法［J］.遥感与导航定位，2012，42(3):34 －37.

［12］冯永新，刘 芳.直接序列扩频信号同步新机理［M］.北京:国防工业出版社，2011:82－90.