遗传算法动态修正核素大气扩散模型的适应度函数研究

吉志龙 马元巍 王德忠

（上海交通大学 核科学与工程学院 上海 200240）

核事故应急支持系统中，核素扩散模型为应急处理提供技术支持，其准确性影响到应急决策是否及时有效。扩散模型中，传统的扩散系数通常采用基于大量扩散实验得到的经验参数。由于事故状态下的风场、大气湍流、地表等与实验条件存在差异，导致经验扩散参数难以准确反映实际的扩散过程。以IAEA和USNRC推荐的Pasquill-Gifford (PG)扩散系数为例，其基于Prairie-Grass-Field (PGF)实验得到[1−2]，适用于多植被地形，摩擦层高度为3cm，近地释放源的情形，通常用于保守预测，如应用于核事故后果评价，其准确性有待提高[3]。

例如在2002年福建惠安核电厂的示踪实验中，根据PG系数得到的扩散参数要明显高于根据实际扩散结果拟合得到的扩散参数[4]。如果核电厂进行了大气扩散实验则以在地的扩散参数为准，但是该扩散参数忽略了大气湍流强度以及温度梯度变化等时序上的变化。

为了使经验扩散参数能更好地反映实际扩散过程，一个可行的办法是以经验参数作为先验值，使用观测数据对其进行动态修正，使得扩散模型计算值与观测值尽可能相近，将经过修正的扩散参数代入原扩散模型后，可以更准确地预测下一阶段核素的扩散浓度分布，这类技术称为源项反演或参数修正。Haupt等[5]首次提出使用遗传算法耦合扩散模型和受体模型，进行源项反演，以达到增强污染物扩散模拟准确度的目的；Jeong等[6]使用类似的技术对核电厂泄露物的扩散进行了分析；Allen等[7]提出了动态修正风场信息，以提高源项反演精确度的技术；Qin等[8]使用源项反演技术分析了英国Dundee地区的空气污染源，对污染物扩散过程进行了模拟。研究表明，源项反演和参数动态修正是增强扩散模型准确性的有效方法，但对于适应度函数和观测误差等影响算法性能的重要方面还缺少进一步研究。本文将通过数值模拟的方法研究适应度函数对参数修正的影响，找出更适合PG参数修正的适应度函数。然后，使用最优适应度函数结合 Kincaid实验数据对扩散模型进行修正，研究修正后的扩散模型预测能力的变化。

1 研究方法

1.1 拉格朗日烟团模型

研究大气扩散模型的参数估计问题，需要扩散模型具有能够模拟变动流场，计算效率高等特点。相对于高斯烟羽模型和蒙特卡洛模型[9−10]，拉格朗日烟团模型更符合此要求[11]，本文采用其作为核素扩散模型。其基本思想为将连续释放的气态流出物简化为连续释放的烟团，每个烟团内的污染物浓度分布符合高斯分布，环境内某点的污染物浓度则为各个烟团在该点浓度分布值的叠加。单个烟团内的浓度分布公式为：

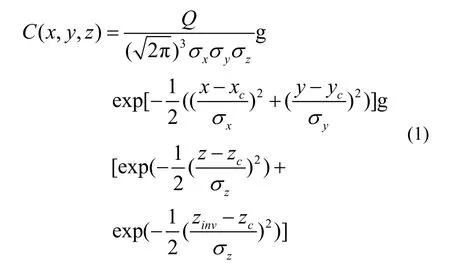
式中，Q为该烟团内放射性物质总活度，Bq·m−3；xc、yc、zc为烟团中心的坐标，m；zinv为逆温层顶的高，m；x、y、z为空间任一点的坐标，m；σx、σy、σz分别为烟团的水平和垂直扩散参数，m。存在多种根据大气稳定度和下风向距离计算这些扩散参数的经验公式，其中最常用的是PG扩散曲线[7]：

式中，x为烟团中心距离释放源的下风向距离，m；py、qy、pz、qz为PG扩散系数，由当时的风速、风向、大气稳定度等信息决定。模型中假设两个水平方向符合相同的浓度分布规律。

1.2 PG参数修正

扩散参数σ是扩散模型中的重要参数，而常用的PG扩散曲线是基于Parairie Grass场地实验数据推导而来的，其使用条件存在一定局限性，当实际情况与PG场地实验条件相差较大时，模型误差较大[8]。为了使扩散模型更好地反映实际扩散情况，可以将原始的PG系数作为先验值，结合观测数据，对原PG系数做修正：

1.3 使用遗传算法修正PG系数

大气扩散模型具有非线性化程度高，参数多等特点，近年来，在基于大气扩散模型的源项反演研究中，使用遗传算法作为最优化过程求解的方法已经取得了一些进展[5−8,12]。

遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，它借鉴了达尔文的进化论和孟德尔的遗传学说，由 Holland教授[13]于1975年首先提出。其本质是一种高效、并行、全局搜索的方法。典型的遗传算法执行流程如图1所示。

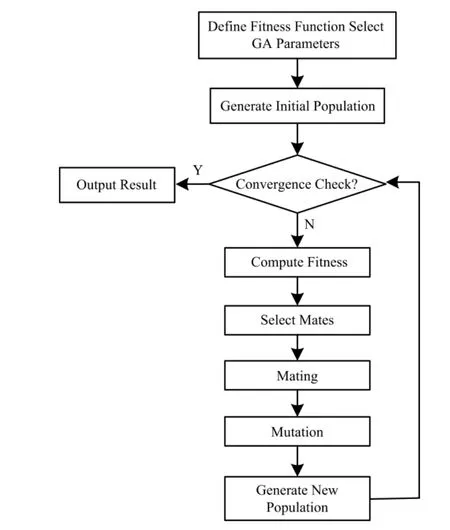
图1 遗传算法流程图Fig.1 Flow chart of genetic algorithm.

图1中遗传算法参数是指种群规模、交叉率、突变率等，其影响了算法的资源消耗率和稳定性。“选择”、“交叉”、“变异”对应于进化论与遗传学说中的自然选择、交配、突变等概念。

2 适应度函数选择

适应度函数对模型计算值和实际观测值之间的差距给出度量标准，是遗传算法修正扩散系数的核心问题。

2.1 可选适应度函数分析

作为模型计算结果与实际测量结果差距的度量，适应度函数值越小则说明两者越接近；另外，不同的观测点，由于所处位置和探测条件等不同，所提供的观测信息的可信度不同，所以适应度函数应符合以下两个原则：

(1) 对于任一监测站i，当│Ci−Qi│增大，即观测值与计算值差距增大时，适应度函数值应增大。

(2) 适应度函数中，不同监测站点的贡献值所占权重可能不同，观测数据越可信，所占权重越大。

对于原则(2)，如果引起监测站探测信息置信度变化的仅为仪器误差，且各站所用仪器的精度一致，则观测值越小，相对误差越大，探测信息的可信度越小。所以原则(2)可简化为对探测值越小的站点，应在适应度函数中给予更小的权重，探测值越大，说明站点越接近扩散流中心，更能反映扩散的趋势，应在适应度函数中给予更大的权重。极端情况下，对于探测数据为零的点，在适应度函数中应不予考虑，因为这样的读数跟离释放源无穷远的点的读数是一致的，该点读数不能为修正PG系数提供有效信息。

基于以上两点，本文在最小二乘法基础上构造并尝试了使用以下4种遗传算法的适应度函数来对PG系数进行修正：

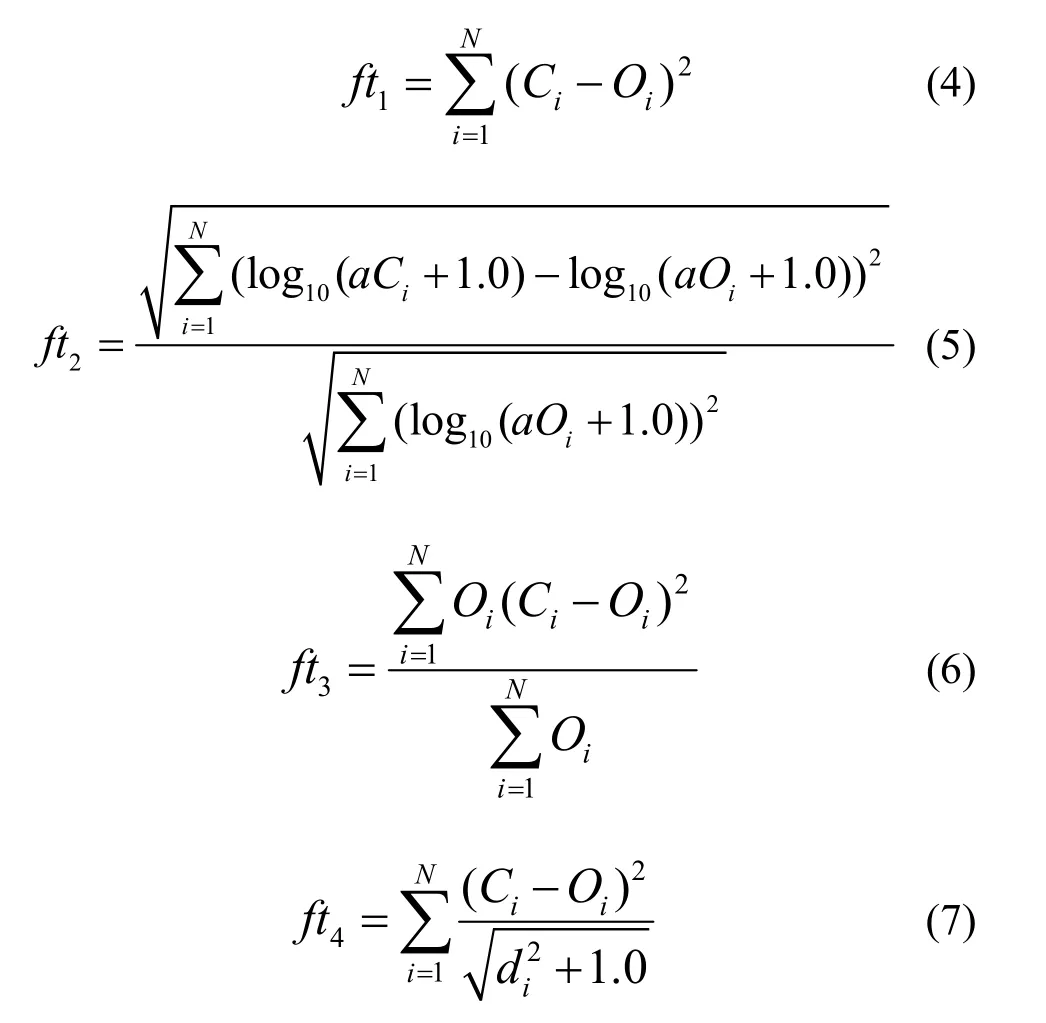
式中，N表示观测点总数；i表示第i个观测点；Ci为扩散模型在第i点的浓度计算值；Oi为第i点的实际测量值；di为观测点i到释放源的距离。ft2中α为常数，用于保证αCi和αOi均大于1。

在这4种适应度函数中，ft1方法简单，对各站点信息进行平权处理，没有考虑观测点误差的影响。ft2由于对浓度进行了对数运算，所以ft2对浓度的指数级变化更敏感。ft3和ft4是对ft1的修正，通常探测浓度越小，或者离释放源越远，则意味着该观测点离释放流的中心距离更远，对于校正模型所提供的信息也越小，故在适应度函数中给予更小的比重。

2.2 数值模拟

本文将采用数值模拟的方法比较4种使用适应度函数对PG系数进行修正的效果，通过设置扩散模型参数，使用扩散模型生成浓度场，并在该浓度场上加入一定噪声以模拟真实测量值，使用“测量值”反演设定的模型参数。

2.2.1 扩散模型参数设置

为简化计算，本文将释放源简化为位于坐标(0,0)的单点源，其距离地表高度为187 m，以9.4 g·s−1的速度释放示踪气体，风场稳定，风向为300°，风速为 3 km·h−1，PG 系数设置为 PGorig：

使用拉格朗日扩散模型计算示踪气体持续释放1 h后的地表浓度分布，结果如图2所示。

图2 扩散1 h后的地表浓度分布Fig.2 Concentrationdistributionsimulated after one hour’s dispersion.

2.2.2 观测点设定

由图2，1 h后由于风向原因，扩散区域主要集中在释放源的东南方向。从该区域均匀抽取24个点作为“观测点”，对这些点上的浓度加入噪声，得到信噪比(signal-to-noise ratio, SNR)分别为无限大（无噪声）、50、5、2.5、0.25 的“观测数据”，分别对应无噪声、小噪声、噪声与信号数量级一致、噪声大于信号情形。信噪比越小，说明监测站的观测误差越大。SNR无限大表示没有加入噪声。

2.2.3 PG系数修正

针对以上得到的“观测值”，使用遗传算法配合不同的适应度函数对PG参数进行修正，为模拟真实情况，对PGorig加入扰动，作为PG参数的先验值PGpre：

针对PGpre，使用遗传算法计算得到使得各适应度函数值最小的最优PG修正系数，将这些修正系数乘以原PG系数后，得到修正后的PG系数PGcorr。比较修正结果 PGcorr与本文设定的 PGorig之间的差异，差异越小，则说明修正效果越好。

2.3 结果分析

通过数值模拟，得到对应于4种适应度函数的4组PQ扩散参数，各自的修正误差由式(10)得到：

由于q在PG参数公式中处于下风向距离x的幂的位置，对扩散参数生成的影响更大，故在式(10)中对p进行取对数处理。理论上，系数修正效果越好，则式(10)的值越小。

4组数值模拟的结果图3所示。由图3，当观测误差很小时，4种适应度函数修正 PG参数的效果相近，随着观测误差增大，ft3和ft4要明显好于前两者，使用ft2的修正效果最差。

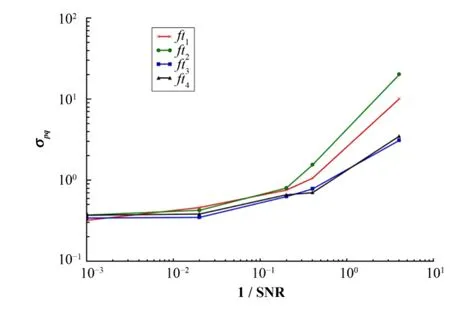
图3 不同适应度函数修正效果随观测误差的变化Fig.3 Correction result of different fitness functions.

结果表明：

(1) 当某个观测点的计算浓度值与观测值差距增大时，4个适应度函数的值都增大，所以当观测条件为理想状态，即观测数据都绝对准确时，它们的修正效果基本一致。

(2)ft1对各监测站数据作平权处理，即假设各站监测数据的可信度是相等的。这只有在测量仪器和测量条件在理想状况下时才能满足。

(3)ft2的关键部分是 log10(aCi+1.0)−log10(aOi+1.0)=log10[(aCi+1.0)/(aOi+1.0)，模型计算误差一定时，Oi越小，适应度函数越大，这违反了原则二，所以当观测误差较大时，ft2的修正效果最差。

(4)ft3和ft4是对ft1的修正，ft3中使用探测值大小做加权，是原则(2)的直观体现。ft4中以观测站到释放源的距离倒数做加权，也体现了原则(2)的思想，因为一般离释放源越远，则扩散浓度值越小。所以当观测误差增大时，这两个适应度函数的表现要好于ft1。

3 示踪实验验证

从数值模拟的结果中可知，使用遗传算法和考虑了观测误差的适应度函数，可以有效地对PG系数进行修正，使其更符合真实的扩散情况。这有助于使用扩散模型预测气载核素的下一步扩散过程，为核应急预警提供信息。本文将使用 Kincaid实验数据来验证PG系数修正对拉格朗日烟团模型预测能力的影响。

3.1 Kincaid实验数据

Kincaid实验是于 1980−1981年在美国伊利诺斯州 Kincaid电厂开展的一项大气扩散实验。实验以六氟化硫为示踪气体，共进行了23组释放实验，每次释放实验持续 3−9 h，分布在距离释放点不同距离段上的监测站在实验中实时记录探测到的六氟化硫浓度[14]。

3.2 验证方法

以1981年5月28日的Kincaid实验结果为例，这组实验共持续了9 h，一共有101个观测站，每个观测站都记录了每个小时末探测到的六氟化硫浓度，同时EPRI 空气质量数据中心提供了实验时详尽的气象数据，本文通过如下方法来验证PG参数校正对模型预测能力的影响：

(1) 对1−8 h内每阶段得到的监测数据，使用标准PG参数作为先验值，ft3或ft4作为适应度函数，经遗传算法对各阶段的 PG参数进行修正，得到 8组修正后的PG参数值。

(2) 将前面得到的8组PG参数修正值做平均，代入拉格朗日扩散模型，计算第9个小时各观测站的浓度值。

(3) 将标准PG参数代入拉格朗日扩散模型，计算第9个小时各观测站的浓度值。

(4) 将第(2)、(3)步中计算得到的第9个小时后各观测站的浓度值与 Kincaid实验记录值做比较。观察使用修正后的PG参数和未经修正的PG参数的扩散模型计算值与真实测量值之间的差异。这里使用统计学量 FA2、BIAS、FB等表征计算值与观测值的相近程度。

3.3 结果分析

通过对Kincaid实验中的20组实验数据作上述验证，将每组实验的统计结果作平均后得到的结果如表1所示。

表1 PG参数修正对模型预测值的影响Table 1 Influence of PG correction on dispersion model’s forecast ability.

FA2的统计意义为 0.5≤C/O≤2，即扩散模型预测值与观测值相差在两倍以内的站点在总站点数中的比例，FA5、FA10类似，这些统计数字越大，则说明模型预测值与观测值更接近；BIAS为平均偏差，其定义为即模型计算平均值与真实测量平均值之差，该值绝对值越小，则说明预测更准确；是平化偏差(Flatted Bias)，其绝对值越小，则预测更准。从表1中可以看出，与直接使用PG扩散参数相比，在拉格朗日扩散模型中使用经遗传算法修正后的PG参数，模型的计算结果与实测结果更相符，模型预测的准确性得到了提高。

4 结语

本文提出了使用遗传算法，利用实时观测数据对放射性核素大气扩散模型中的经验扩散参数进行实时修正，以增强扩散模型准确性的方法。通过数值模拟，对比分析了使用遗传算法对拉格朗日大气扩散模型中的 Pasquill-Gifford扩散系数进行修正时，4种适应度函数的修正效果。结果表明，使用考虑了观测误差和观测站距离等影响的适应度函数

ft3和ft4对PG系数修正的结果更接近于真实值。将在数值模拟中表现占优的ft3和ft4应用到Kincaid实验数据集发现，使用遗传算法对PG系数进行修正后，扩散模型的预测能力得到了提高。

1 IAEA. Atmospheric dispersion model for application in relation to radionuclide release[M]. Austria: International Atomic Energy Agency, 1986

2 USNRC. Methods for estimating atmospheric transport and dispersion of gaseous effluents in routine release from light water cooled reactor[M]. Washington: Nuclear Regulatory Commision, 1977

3 Venkatram Akula. An examination of the Pasquill-Giffrd-Turner dispersion scheme[J]. Atmospheric Environment, 1996, 30(8): 1283−1290

4 胡二邦, 幸存田, 宣仁义, 等. 福建惠安核电厂址 SF6示踪实验研究[J]. 环境科学学报, 2004, 24(2): 320−325 HU Erbang, XING Cuntian, XUAN Renyi,et al. The SF6 tracer study in the Fujian Huian nuclear plant[J]. Acta Scientiae Circumstantiae, 2004, 24(2): 320−325

5 Haupt S E, Young G S, Allen G T. Validation of a receptor-dispersion model coupled with a genetic algorithm using synthetic data[J]. Journal of Applied Meteorology and Climatology, 2006, 45(3): 476−490

6 Jeong H J, Kim E H, Suh K S,et al. Determination of the source rate released into the environment from a nuclear power plant[J]. Radiation Protection Dosimetry, 2005,113(3): 308−313

7 Allen C T, Young G S, Haupt S E. Improving pollutant source characterization by better estimating wind direction with a genetic algorithm[J]. Atmospheric Environment,2007, 41(11): 2283−2289

8 Qin Y, Oduyemi K. Atmospheric aerosol source identification and estimates of source contributions to air pollutions in Dundee, UK[J]. Atmospheric Environment,2003, 37(13): 1799−1809

9 闫政, 吴信民, 邓磊, 等. 使用蒙特卡罗方法模拟核事故气载放射性污染物大气扩散[J]. 核技术, 2011, 34(3):193−198 YAN Zheng, WU Xinmin, DENG Lei,et al. An M-C model to simulate airborne radioactive material dispersion in nuclear accident[J]. Nuclear Techniques, 2011, 34(3):193−198

10 Turner D B. Workbook of atmospheric dispersion estimates: an introduction to dispersion modelling[M].Florida: Lewis Publishers, Boca Raton, 1994

11 Raza S, Avila R, Cervantes J. A 3D Lagrangian particle model for the atmospheric dispersion of toxic pollutants[J].International Journal of Energy Research, 2002, 26(2):94−95

12 宁莎莎, 蒯琳萍. 混合遗传算法在核事故源项反演中的应用[J]. 原子能科学技术, 2012, 46(z1): 469−472 NING Shasha, KUAI Linping. Back-calculation of source terms by hybrid genetic algorithm in nuclear power plant accident[J]. Atomic Energy Science and Technology, 2012,46(zl): 469−472

13 Haupt R L, Sue Ellen Haupt. Practical genetic algorithms[M]. New Jersey: John Wiley & Sons, Inc, 2004:23−24

14 Olesen H R. User’s guide to the model validation kit[M].Denmark: National Research Institute, 2005: 18−26