关于矩阵特征值应用的探索

邓亮章

(福建信息职业技术学院基础教学部，福建福州350003)

1 引言

简单地进行矩阵的特征值的求解是一件非常容易的问题，然而，将矩阵的特征值应用到其它的领域之中就变得不再是那么容易了。矩阵的特征值在众多的领域中都存在着非常广泛的应用，能够解决众多的实际问题。因此，矩阵的特征值的应用具有非常重要的意义。文章将首先简单地概述矩阵的特征值的相关概念;然后，在此基础上，深入地探索矩阵特征值在数学建模问题方面的应用，通过具体的例子来详细地阐述矩阵特征值的应用。

2 矩阵的特征值的相关概念

定义1 假设Ψ是数域P上线性空间V的一个线性变换，倘若对于数域P中的一个数λ0，存在一个非零向量ξ，使得

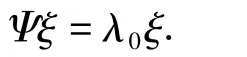
那么，λ0称为Ψ的一个特征值，而ξ称为Ψ的属于特征值λ0的一个特征向量。

定义2 假设A是数域P上的一个n级矩阵，λ是一个数，矩阵λE-A的行列式

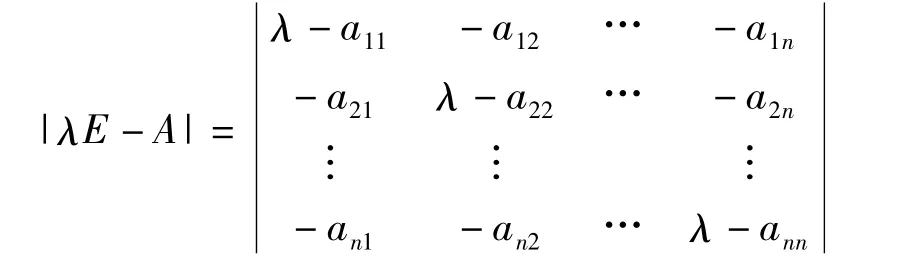
称为矩阵A的特征多项式，其中矩阵A的特征多项式的根就是矩阵A的特征值。

3 矩阵的特征值的应用

在数学建模问题中，会涉及到非常复杂的高次计算，而矩阵的高次计算对于数学建模问题的解决会造成一定的困难，在这种情况下，就应该借助于矩阵的特征值及其特征值向量，来非常科学有效地进行解决，将看上去复杂的矩阵转变成简单的对角阵，保证运算变得更简单。

Fibonacci数列是非常经典的。在1202年，斐波那契在一本书中提出一个问题:如果一对兔子出生一个月后开始繁殖，每个月生出一对后代，现有一对新生兔子，假定兔子只繁殖，没有死亡，问第K月月初会有多少兔子?

以”对”为单位，每月兔子组队数构成一个数列，这便是著名的 Fibonacci数列{Fk}:0，1，2，3，5，…，函数数列能够符合条件

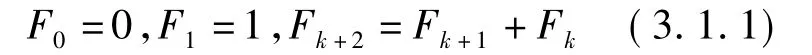
请经过计算得到通项Fk.

解:由Fibonacci数列能够符合(3.1.1)式，假设

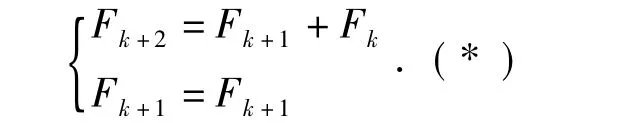
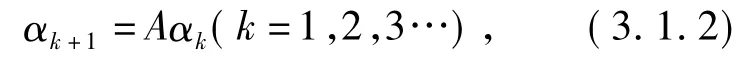
由(3.1.2)式进行递归能够得到:

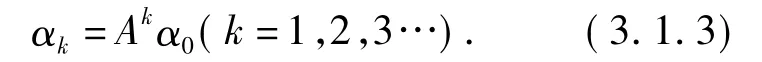
因此，计算Fk的问题就转化成计算αk，也就是说，计算Ak的问题.由

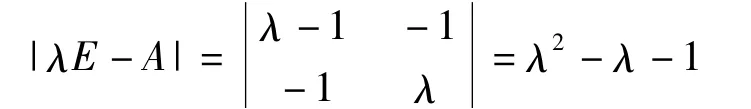
得A的特征值

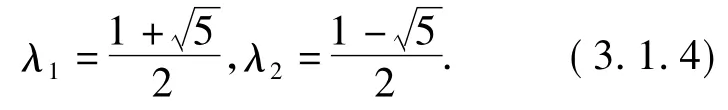
对应于λ1，λ2的特征向量各自是:

因此，可以得到:

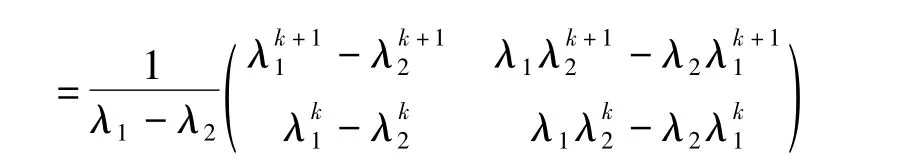
因此，可以得到:

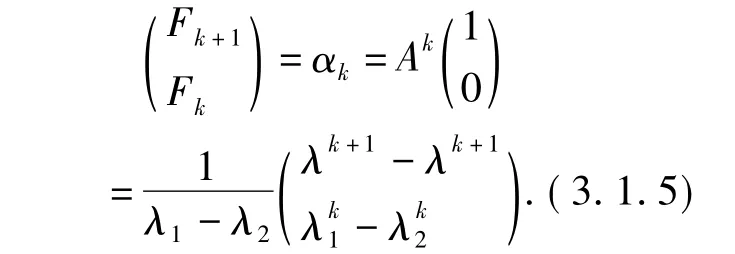
将(3.1.4)式代入(3.1.5)式，可以得到:

4 结语

综上所述，矩阵的特征值问题是一类非常重要的高等数学问题，在众多的领域中都取得了非常广泛的应用，文章结合具体的实例深入地研究了矩阵特征值在数学建模问题以及一阶线性常系数微分方程组方面的应用。通过研究能够发现，其主要作用是将矩阵对角化，通过这种方式，进一步就能够对矩阵进行高次运算，在此基础上，可以简化计算的复杂度，与此同时，由于矩阵的特征值这一特性，也促使矩阵的特征值在工程设计、动力学等方面都取得了非常广泛的应用.

［1］田应福.Schur余阵的一个不等式及其应用［J］.安顺师专学报，1999，(2).

［2］李修清.关于矩阵展形的新估计及其应用［J］.四川师范学院学报(自然科学版)，1996，(4).

［3］李修清.矩阵秩的下界估计［J］.青海师范大学学报(自然科学版)，1993，(2).

［4］王其申.关于正矩阵的最大特征值的包含定理及其应用［J］.高等学校计算数学学报，2000，(2).