一类无序细胞结构模型的研究与实现
2014-10-13左常玲傅廷亮郭丁云孙志峰
左常玲,傅廷亮,郭丁云,孙志峰
(安徽三联学院, 合肥 230601)
1 引 言
在无序细胞结构类计算机仿真中常常使用Voronoi结构做为初始模型,图1所示的二维Voronoi图的定义是: 在平面上随机地撒下n个点,这n个原始点将是n个多边形的中心(在仿真时也常称为细胞核).选定某一点作为参考点,以该点为起点做与其它n-1个点的连线,再作这n-1根连线的垂直平分线,这些垂直平分线必然相交,只有那些围绕参考点的垂直平分线围成所需要的多边形,即这个多边形内只有唯一的一个参考点做为中心点.重复以上过程,依次用其它n-1个点形成n-1个多边形,从而构成一个含有n个多边形的二维随机结构模型[1][2].
目前Voronoi结构得到了广泛应用,例如在自然界中各种各样的生物细胞结构、各种液体泡沫和化工材料等领域都有应用.Zachariase提出另一类模型做为玻璃材料的模型,该模型与voronoi模型相似,它以小三角形顺时针螺旋形围绕而形成各个多边形,而由这些多边形构成了另一类网格模型.图2是该类模型的一个例子[3-4].

图2 一个Zachariase模型
2 Zachariase模型算法
从图2可看出玻璃结构模型与Voronoi多边形结构相似,不同之处是所有多边形的边长都相等,各边长等于小三角形的边长.同样也要分析其面积和边的分布函数,以及它们之间的相关性,由图2可见,这些多边形的边数大多取4至8条边中的某个值.普通的Voronoi图可以用细胞生长法或几何法等方法生成,并且以离散的点为初始生成元.在这里,我们借鉴Voronoi图的形成方法,但不是先形成各多边形的中心点,而是将初始生成元设为大小固定的正三角形,并且使用几何法生成[5-6].
使用正三角形形成上述模型有一些优点,使得它可以方便地应用于玻璃结构的模拟.1873年,Plateau根据能量最小化原则提出有关肥皂泡几何形状Plateau定律,其中,在二维情况下,一个顶点只能有三条边相交,它们相互间的夹角相等,必为120°.在玻璃模型结构中,Voronoi图的生成元正好可以从随机顶点异化为正三角形.只不过,它仍然有一些不等于120°的顶角,而且边的分布也比较窄.
为了区别于通常Voronoi方法,我们通过一个迭代过程方法生成二维玻璃模型.当然,迭代过程同样必须保证充分的随机性,从而达到与平面撒点的几何法一样的效果,并获得算法的简化和性能的改善.
最初,Zachariasen提出如下的玻璃模型:在平面上放置一系列的等边三角形,这些三角形顶点互连但不重叠,它们以顺时针旋转的方式围绕着平面上随机种子点首尾相接形成一个多边行环.图3是小三角形重叠的例子.

图3 小三角形重叠不能形成可用的模型
之后,Shackelford又提出了一种扩展模型,这种模型给出一个更窄的边数分布,它允许把直线当做正三角形一样参与多边行环的构成.由于篇幅限制,本文不讨论这种扩展模型.
为了实现Zachariasen以三角形为基本单位进行环绕生成邻居多边形的算法,本文实现的算法是以多边形为基本环绕单位,在此基础上形成图2所示的多边形网络,其基本流程是:
1)初始化.
2)随机添加一个安全的多边形(所谓“安全”,即满足图2模型,不出现三角形叠加,并且符合细胞结构的边数和拓扑结构要求).(见图4(a))
3)以多边形各边为基础,每边都补上三角形.(见图4(b))
4)随机选取下一个添加多边形的位置,继续环绕补足下一个多边形,转(2)(见图4(c))直到生成的细胞数目满足要求时,算法终止.
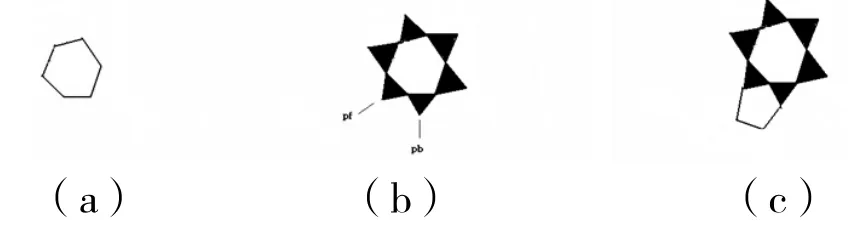
图4 形成一个多边形的示意图
每一步我们都随机地在数字4至8中选择一个数作为多边行环的边数.如果边数小于4,容易导致系统崩溃;边数大于8,对于建模来说,并不增加太多的额外负担,但模拟结果就会使得各“细胞”边数和面积差异变大,不符合Zachariase模型的要求.采用顺时针方向作为模型构建的主方向,多边形的生成,三角形的生成以及整个图的生成过程都沿顺时针方向进行,由此引入向前边函数检查和向后边函数检查,以确保添加的边或三角形是安全的.
3 Zachariase模型的程序实现
如果要形成有n条边的多边形,按顺时针方向形成n-2条边的未封闭凸环后,还缺少构成封闭凸环的最后两条边.由于模型中多边形边数只能是4~8边,在已调用sides_random()函数产生了两条边后(本节后面介绍sides_random()函数),则再添加的边数为以下四种情况之一.
case 2: 随机sides_random()产生:(环端距poledis/△ 边长edgelength+1+2~5)
如果结果是:
case 3:检查poldis=edgelength,是,则连上第3边;不是,出错
case 4:别无选择,只能组成菱形
case 5:关键是随机edge_random()产生第3边的选择,第4、5边别无选择,只能取中垂线作图
case 3:随 机 random()产 生 :(poledis/edgelength+1+3~6)
如果结果是:
case 4:检查poldis=edgelength,是,则连上第4边;不是,出错
case 5:别无选择,只能取中垂线作图
case 6:关键是随机edge_random()产生第4边的选择,第5、6边别无选择,只能取中垂线作图
case 4:随机random()产生:(poledis/edgelength+1+4~7)
如果结果是:
case 5:检查poldis=edgelength,是,则连上第5边;不是,出错
case 6:别无选择,只能取中垂线作图
case 7:关键是随机edge_random()产生第5边的选择,第6、7边别无选择,只能取中垂线作图
case 5:随机random()产生:(poledis/edgelength+1+5~8)
如果结果是:
case 6:检查poldis=edgelength,是,则连上第6边;不是,出错
case 7:别无选择,只能取中垂线作图
case 8:关键是随机edge_random()产生第6边的选择,第7、8边别无选择,只能取中垂线作图
程序中两个典型的数据结构是小三角形的数据结构和多边形的数据结构.小三角形的数据结构:
class triangle
{
属性:(private)
double x[4];//其中x[0],y[0]为小三角形的中心坐标,其余为三个顶点坐标
double y[4];
bool edgestate[3];//三边各自状态,是否已经配对
int neibour[9];//neibour[0/1/2]表示邻居多边形及与构成该多边形的两个邻居小三角形的数组下标,neibour[3/4/5]和neibour[6/7/8]类似于neibour[0/1/2]的描述
}triangle[800];
多边形的数据结构:
class polygon
{
int sides;//边数
int neibourtri[8];//(至多8个)邻居小三角形的数组下标
}polygon[200]
edge_random()函数是一个关键的函数,它必须考虑每随机扩展一条边(一个小三角形),都有可能导致后面的顺时针弧无法形成凸多边形.edge_random()函数内的条件限制有:每个三角形有且仅有三个邻居,构成凸多边形的相邻的两条边夹角为[60°,180°],同样,推广到任意两个三角形的邻边夹角也为[60°,180°],小三角形的两个邻居三角形的“距离”应该大于edgelength.如图5所示,最下面两个三角形距离过近是不允许的(虽然两个夹角都大于60°,符合角度要求),每次扩展一个凸多边形时,最后两条边总是别无选择的,只能取中垂线作图.如果最后两条边作完后发现与前几条规则有冲突的话,则必须往回调整以前随机产生的边的夹角.
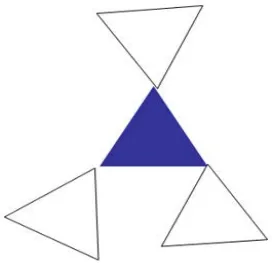
图5 一次失败的图形生成
4 仿真结果
本文系统的仿真结果见图6所示,图中给出四个二维模型图,由于在图中对多边形边数做了限制,可知这类多边形网络的边数分布二次矩不会太大,也不会太小.(见图6中的四个图例)边数分布二次矩定义如下,其中n是多边形的边数,f(n)是图中多边形的边数分布函数.


图6 使用本文系统产生的几个仿真模型
5 结束语
二维玻璃模型是无序细胞结构的一类模型,与Voronoi模型相比有其自身的特点.由于玻璃材料结构的无序特点,影响其结构的因素很多,故Zachariase的玻璃结构模型可以作为一种研究方法,它简化了此类模型的生成,为使用计算机程序仿真这类材料提供了一种新手段.
[1]傅廷亮.计算机模拟技术[M].合肥:中国科学技术大学出版社, 2001:21-32.
[2]Weaire D and Fu T L.The Mechanical Behavior of Foams and 3Emulsions [J].Journal of Rheology , 1988, 32(3):271~283.
[3]Glazier J A, Gross S P and Stavans J.Dynamics of Two-Dimensional Soap Froths [J].Physical Review A, 1987,36:306-312.
[4]Shackelford J F.Triangle Rafts-Extended Zachariase Schematics for Structure Modeling[J].Journal of Noncrystalline Solids,1982, 49:19-28.
[5]车武军,杨勋年,汪国昭.动态骨架算法[J].Journal of Software,2003, 14(4):818-823.
[6]杜永强,李清玲.多连通域Voronoi图是算法及数据存储结构[J].计算机工程与设计, 2006,27(8):1468-1471.
[7]James Alexander Glazier.Dynamics of Cellular Patterns [D].The University of Chicago, Chicago Illinois, 1989:91-98,189-191.
