锥形流化床水平射流条件下的流化特性

祝小龙，刘代俊，陈建钧

（四川大学化学工程学院，四川 成都 610065）

流化床技术现今已被广泛运用于化工、石化、冶金、能源、环保、制药等领域。与传统的燃烧、反应设备相比，流化床具有混合均匀、反应速度快、气固接触面积大、传热、传质系数高、反应温度均匀、单位面积的反应强度大、操作易于控制、物料在反应器中停留时间可调、生产能力大等优点。正是由于流化床技术的迅速发展与应用，吸引了很多研究者对流化床内流化特性进行分析研究。而在锥形流化床中，除了具备一般流化床的优点以外，由于其截面随高度而变化，所以存在着流速梯度：在底部截面较小，因而流速较高，可保证大颗粒的流化；而在顶部截面较大，所以流速较低，可防止小颗粒的带出，因此可避免热集中在底部而使固体物料烧结，并可避免使用分布板。

随着锥形流化床在颗粒干燥、悬浮和包涂等领域的广泛应用[1-2]，人们对其流化特性进行了广泛研究。Peng等[3]主要研究了液-固锥形流化床特性，其余学者对气-固锥形流化床的特性也进行了大量的研究[4-6]，但都主要研究气体垂直向上射流情形下流区特性以及流区内压降与表观气速之间的关系等，而对于锥形流化床中水平射流的研究相对较少。采用水平射流的方式形成撞击流，产生一个高湍流区，极大地强化相间传递，使其具有优越的微观混合性能[7-8]，同时防堵、防止涡流。另外，床内流体产生摆动效应，若改变进气喷嘴的入射角度，还可产生漩涡[9]。这些特点是一般流化床或喷动床不能相比的，目前主要用于氯化钛白的生产上。本文通过在一个二维锥形流化床中，从底端两侧水平进气口通入流化气体，对二维流化床的流动情况进行了研究，着重分析了床层压降随表观气速变化的关系，以及对最小流化速度和床层最大压降计算公式进行推导，并与实验结果进行比较。

1 实验方法

1.1 实验设备

为了更加直观地观察气、固两相在锥形流化床中的运动规律，采用无色透明的有机玻璃面板构成的二维床结构为实验装置，如图1所示。锥形流化床所需的流化介质为空气，由空压机提供。二维流化床床体上部为400 mm×300 mm×30 mm（高×宽×厚）的长方体；下部为160 mm×300 mm(20)×30 mm（高×宽×厚）、锥角为 60°的锥体。锥体底端两侧设有两个圆形水平喷头，喷头内径为 4 mm；锥体背面中轴线上钻有间距 80 mm的小孔，孔径为 6 mm，这些孔是床层压力信号的测点。

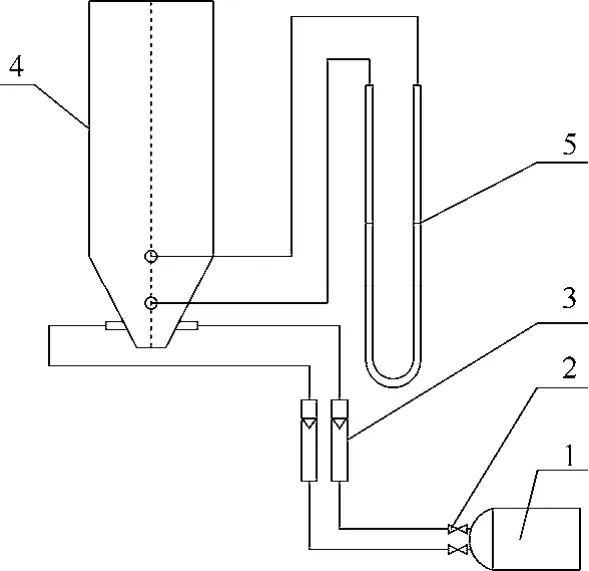
图1 实验装置流程图

1.2 实验物料

本研究采用了3种不同粒径的圆形玻璃珠作为实验物料，流化介质为空气，物料的特性见表1。

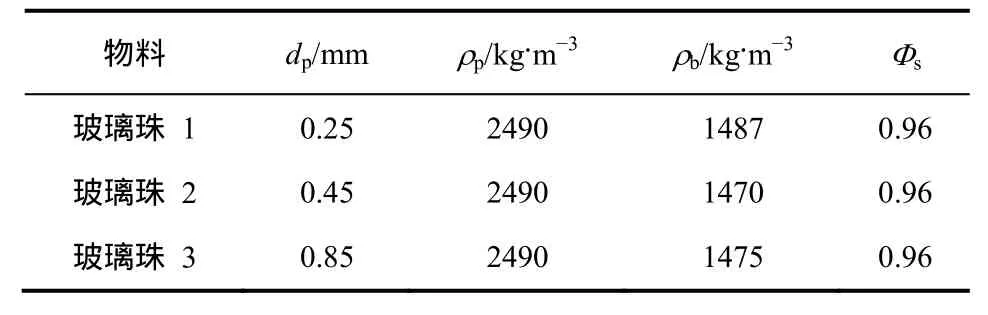
表1 颗粒物料性质

1.3 实验方法

进行实验时，首先确定一个气体流量条件，并保持4～5 min，使得整个床达到稳定状态，观察床中的物料状态，并记录下两侧进气流量计的读数和所测量的压降。实验过程中，两侧进气量始终保持一致。由于升速法所得的压降曲线因为迟滞效应而带有任意性，故本实验在先调到最大气量后，逐渐减小气体流量，并重复上述的操作。实验条件：3种玻璃珠物料粒径分别为0.25 mm、0.45 mm、0.85 mm，每种物料初始填料体积分别为0.7 L、0.8 L、0.9 L、1.0 L。

2 结果与讨论

2.1 实验现象

锥形床的流体力学特性如图2所示，随着两侧进气流量的同时降低，颗粒间孔隙率ε逐渐减小，导致床层的压降缓慢升高；直到临界流化状态时，床层的总压降达到最大值maxPΔ；进一步降低流化流量，颗粒转变为固定床，其压降将迅速降低。

2.2 最小流化速度和最大压降

本实验通过观察锥形床中物料的流化行为，发现当进气量达到一定值后，床层中心出现了十分明显的“沸腾核心”区域，而在沸腾区域和锥形床两侧壁面之间具有向下移动的环形截面料层。

为了能够在数量上计算锥形流化床的流体力学特性，首先应求得在临界状态时，颗粒物料由固定态过渡到流化态瞬间流速沿床层高度变化的规律性。考虑到锥形床中存在明显的沸腾区域和环形截面料层，本实验假设，当颗粒物料处于临界状态时也像进入流化状态后一样，流体并不沿设备的整个截面通过，而是通过具有某一锥角的通道流过床层，如图3所示。

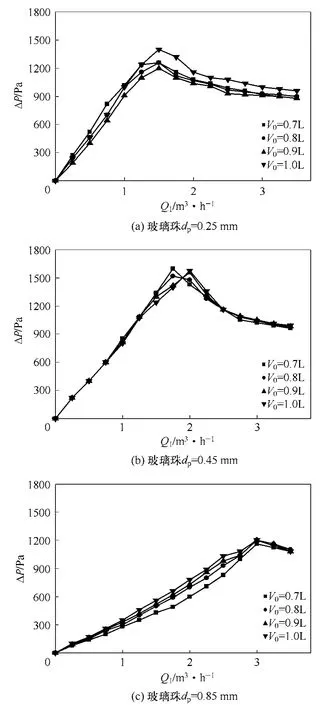
图2 单侧进气流量对压降的影响

通过以上的假设，在二维锥形流化床中，根据物料守恒，得到式（1）。

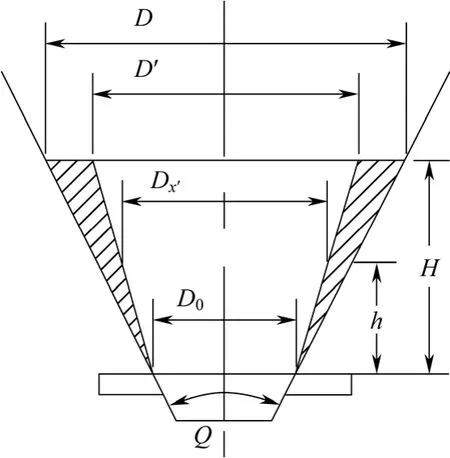
图3 锥形床参数示意图

当锥形床上截面流体通道内的流速达到临界速度 umf时，床内颗粒就进入流化状态，由此可得式（3）。

因此，当二维锥形床全床进入流化状态时，颗粒物料的最小流化速度为式（4）。

秦霄光等[10]在前人研究的基础上，发现当锥形床锥角 α ＞20°时，见式（5）。

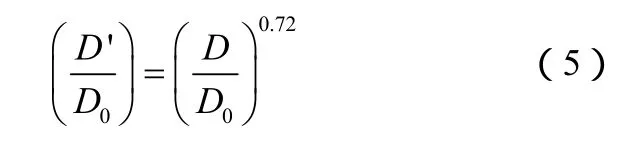
而实验所采用锥形床锥角α为60°，测得底端两进气口所在床层截面宽度0D为0.07 m，通过在实验过程中测量D与 'D对比发现，结果与秦霄光等的研究比较接近。实验测得数值比较见图4。

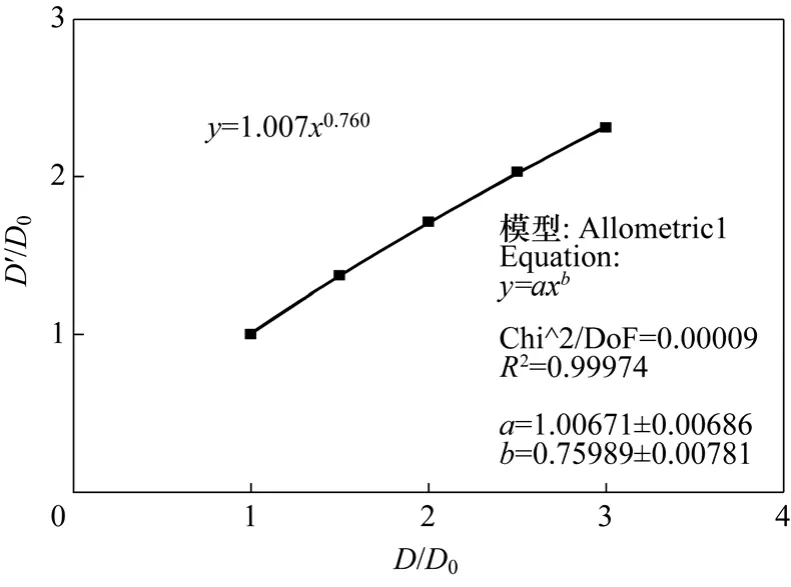
图4 数值比较

根据图 4，在所研究的锥形二维流化床中，结合秦霄光等[10]的研究成果，采用Allometric1方程拟合，得到以下关系，如式（6）。

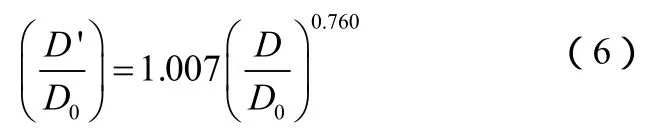
为了便于计算，近似简化为式（7）。

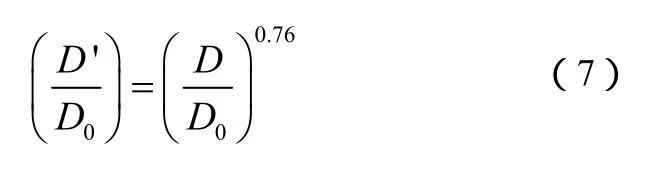
将以上式子整理得，颗粒物料最小流化速度见式（8）。

而当床内颗粒达到起始流化状态时，流速沿床层高度的变化规律为式（9）。

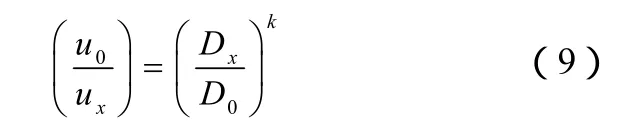
式中，k为常数，其值为0.76。

在求出锥形流化床最小流速气速之后，可以计算出临界状态时的最大压降maxPΔ。

根据前人对锥形床通过底部喷嘴竖直向上进气条件下的研究[11-12]，假设在整个流体通道横截面上流体速度相同，沿床层的轴向总压降由Ergun公式关联，见式（10）～式（12）。

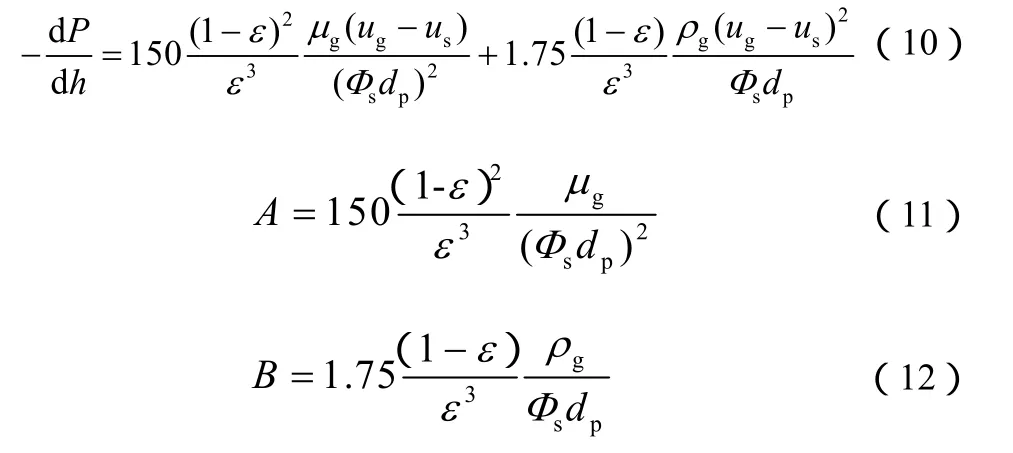
在本实验中，s1Φ≈，s0u=，式（10）简化为式（13）。

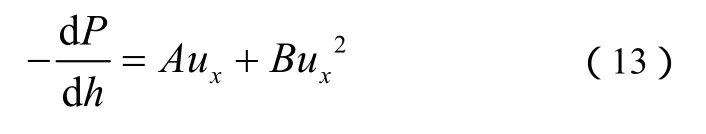
在“沸腾核心”假设的基础上，将式（9）带入式（13），同时将Dx化成填料高度h的函数，积分可得式（14）。

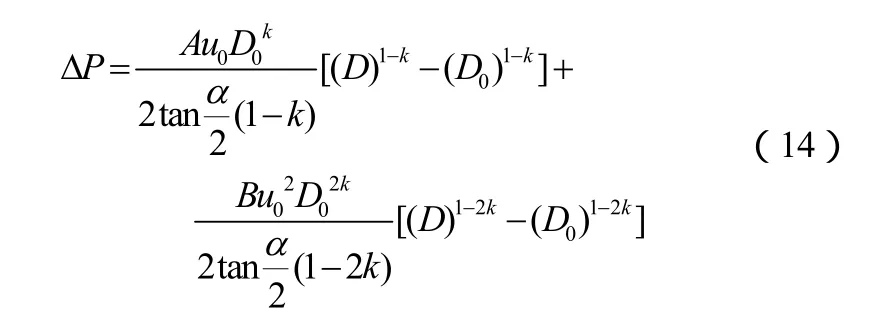
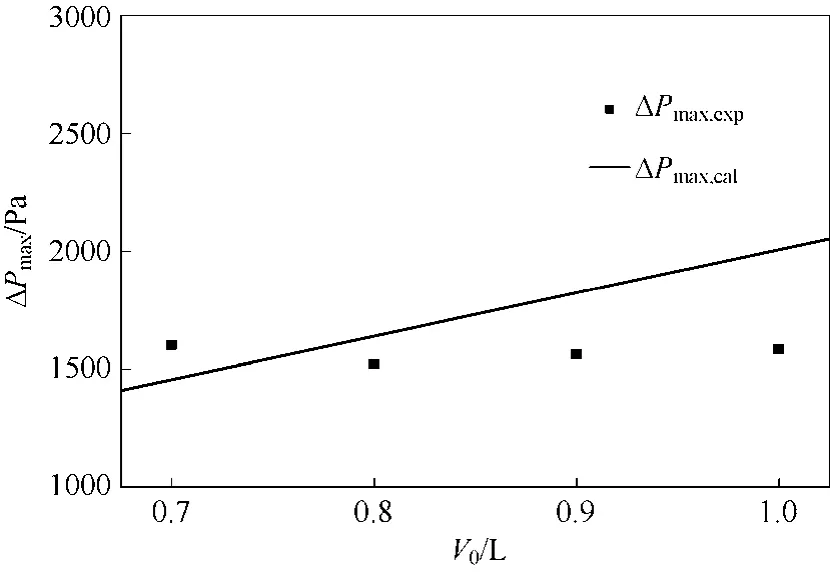
图5 最大压降的实验和计算结果比较

通过式（8）计算出umf带入式（14）中算出maxPΔ。将求的的压力值与实验测得值相比较，如图5所示。

结果表明，对于实验研究锥角60°的二维锥形流化床，通过Ergun公式求得的最大压降maxPΔ要比实验测定值整体上偏大，这可能是因为本文在提出“沸腾核心”观点的同时，将锥形床上截面流体通道内的临界速度u定义为锥形床的最小流化速度umf，即当核心部分物料面上的流速达到物料的“沸腾”速度时，才由固定床转化为流化床，而锥形床在轴向上存在速度梯度，当料面上的流速达到“沸腾”时，全床已处于剧烈运动中。因此，在实际操作中，实验测得的最大压降要比计算所得的压降小。同时，因为实验是在水平射流条件下操作的，相比于竖直向上射流的锥形床，两端进气水平气流进行对流，气流通过撞击的方式强化了传质，同时产生较大气泡，加快了床层的“沸腾”，因此使得最大压降maxPΔ的实验值小于计算值。实验值与计算值的这种差异和关系还有待进一步研究。

2.3 最小流化速度的影响因素

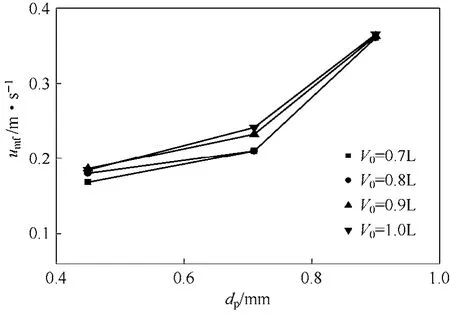
图6 最小流化速度与颗粒粒径的关系

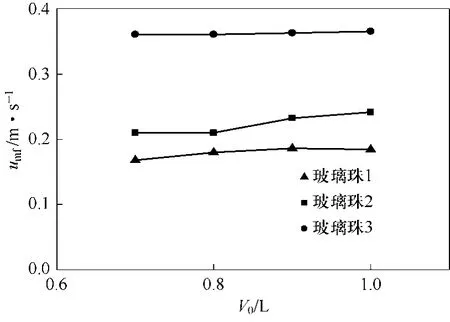
图7 最小流化速度与填料体积的关系

图6显示了各操作条件下床层颗粒粒径对最小流化速度的影响。从图6中可以看出，在相同填体积条件下，颗粒粒径小的先流化。因为随着颗粒直径的增大，该颗粒的终端速度也相应增大，从而导致最小流化速度增大。

图7显示了各操作条件下床层填料体积对最小流化速度的影响。从图中可以看出，起始流化速度随填料体积的增加而略有增加。这是因为填料体积越大，高度越高，流动阻力越大，导致所需的最小流化量增大。增大趋势不明显可能是因为填料体积增幅不大，导致所需的起始流化气量变化大。

3 结 论

（1）二维锥形流化床在水平射流进气条件下，床层压降随流量增大而迅速升高，达到一个最大值后略有下降。

（2）二维锥形床中，当床内颗粒达到起始流化状态时，流速沿床层高度的变化规律为式（9）。

（3）对于水平射流条件下的锥形流化床，在“沸腾核心”假设基础上，根据Ergun公式计算得到的最大压降maxPΔ要比实验值整体偏大。

（4）二维锥形流化床的最小流化速度随颗粒粒径增大而增大，随填料体积的增加也略有增大。

符 号 说 明

A —— 欧根方程中的常数

B —— 欧根方程中的常数

D —— 料面流体通道截面设备宽度，m

D' —— 料面流体通道截面宽度，m

D0—— 进气口处截面设备宽度，m

Dx—— 距进气口截面任意距离h处设备的宽度，m

Dx' —— 距进气口截面任意距离h处流体截面宽度，m

dp—— 颗粒直径，mm

k—— 常数0.76

ΔPmax—— 床层最大压降，Pa

u0—— 进气口处截面流体速度，m/s

ug—— 气体速度，m/s

umf—— 最小流化速度，m/s

us—— 颗粒速度，m/s

ux—— 距底端进气口截面距离h处流体速度，m/s

V0—— 初始填料体积，L

α—— 锥形床锥角，（°）

ε—— 床层孔隙率

μg—— 气体黏度，Pa/m

ρb—— 颗粒的堆密度，kg/m3

ρg—— 气体密度，kg/m3

ρp—— 颗粒密度，kg/m3

Φs—— 颗粒球形度

下角标

cal—— 理论计算值

exp—— 实验值

[1]Deiva V R，Chaouki J，Klvana D. Fluidization of cryogels in a conical column[J]. Powder Technol.，1996，89：179-186.

[2]Olazar M，San Jose M J，Aguayo A T J，et al. Stable operation conditions for gas-solids contact regimes in conical spouted beds[J].Ind. Eng. Chem. Res.，1992，31：1784-1792.

[3]Peng Y，Fan L T. Hydrodynamic characteristics of fluidization in liquid-solids tapered beds[J]. Chem. Eng. Sci.，1997，52（14）：2277-2290.

[4]Olazar M，San Jose M J，Aguayo A T，et al. Pressure drop in conical spouted beds[J]. Chem. Eng. J.，1993，51：53-60.

[5]Olazar M，San Jose M J，Llamosas R，et al. Hydrodynamics of sawdust and mixtures of wood residues in conical spouted beds[J].Ind. Eng. Chem. Res.，1994，33：993-1000.

[6]Bi H T ，Macchi A，Chaouki J，et al. Minimum spouting velocity of conical spouted beds[J]. Can. J. Chem. Eng.，1997，75 （4）：460-464.

[7]伍沅. 撞击流的特性和应用[J]. 化工进展，2001，20 （11）：8-13 .

[8]张建伟，伍沅，舒安庆. 浸没循环撞击流反应器压力波动研究[J].化工学报，2005 ，56（2）：266-269.

[9]许建良，李伟锋，曹显奎，等. 不对称撞击流的实验研究与数值模拟[J]. 化工学报，2006，57（2）：288-291 .

[10]秦霄光，邱信淼，陈洪生，等. 聚式锥形流化床流化特性[J]. 化学世界，1964（8）：380-381.

[11]胡庆元，景山，王金福，等. 粗颗粒在锥型床中的流化特性[J]. 高校化学工程学报，2000，14（1）：12-18.

[12]蔡国斌，汪展文. 细粉在锥型床中流态性能的研究[J]. 青海大学学报，2001，19（1）：25-28.