超额吉布斯自由能-状态方程模型的研究进展

兰雪，夏力，项曙光

（青岛科技大学炼油化工高新技术研究所，山东 青岛 266042）

相平衡的计算有两种方法，即状态方程法和活度系数法。状态方程法可以适用于压力范围较大的相平衡计算。针对混合物的相平衡进行计算中，必须使用相应的混合规则。对于强极性体系和强不对称体系，状态方程法使用传统的混合规则会产生较大的误差。活度系数法通常对低压下的简单和复杂化合物都有较好的应用，而且可以预测相平衡。但是由于交互作用参数的缺少，活度系数法不适用于高压的情况。超额吉布斯自由能-状态方程（GE-EoS）模型使用活度系数 GE模型计算得到混合规则，把状态方程法和活度系数法结合起来，扩大了状态方程的使用范围。

1 GE-EoS模型的主体思想

GE-EoS模型的主体思想是：状态方程计算出的超额吉布斯自由能等于活度系数模型计算出的超额吉布斯自由能，如式（1）所示。

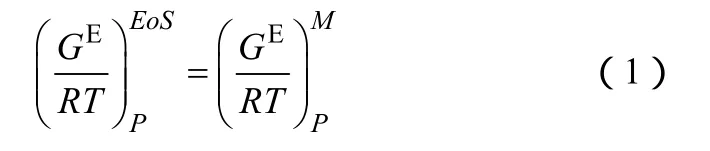
以SRK方程为例，由状态方程导出的超额吉布斯自由能如式（2）所示。

以式（3）计算得到b，将b带入式（2），可以得到a关于GE的表达式，如式（4）。

式（4）中的GE以活度系数模型计算，这样就将状态方程和活度系数模型结合了起来。式（4）和式（2）即为得到的GE-EoS模型。

2 GE-EoS模型

自从HV混合规则提出后，GE-EoS模型发展迅速。目前已经有很多优秀的 GE-EoS模型应用于工业中的汽液相平衡计算和化工过程模拟软件[1]。

为了得到简单的GE混合规则，GE-EoS模型的参考压力大多选择无穷压力或者是零压力。

2.1 以无穷压力为参考态的GE-EoS模型

以无穷压力为参考态的 GE-EoS模型，最著名的是HV混合规则和WS混合规则。

2.1.1 HV混合规则

Huron和Vidal[2]提出了HV混合规则。HV混合规则作了两点假设。

（2）在无穷压力下，超额体积为零。

这一点假设就限定了 b必须使用线性混合规则，即式（3）。

根据以上两点假设和式（1），可以得到HV混合规则的一般形式如式（5）。

式（5）中的C为与状态方程有关的参数，EPG→∞为无穷压力下的超额吉布斯自由能。

HV混合规则是第一个提出的GE-EoS模型，它与传统的范德华混合规则相比，大大地扩大了状态方程的使用范围。Vidal等[2-3]曾使用HV混合规则结合SRK状态方程和NRTL模型对丙酮/水、丙酮/环己烷、甲醇/CO2、乙烷/丙酮、丙烷/乙醇和一些其他的复杂混合物体系进行汽液相平衡关联，得到了非常好的结果。

已知GE可以写成如式（6）的形式。

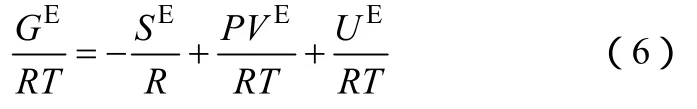
由 HV混合规则的第一个假设可以得到 SE为零，HV的第二个假设是 VE为零。式（6）变成把 UNIFAC等活度系数模型分为组合项和剩余项，所以在无穷压力下 GE本质上反映的是超额吉布斯自由能剩余项的贡献。

Lermite等[3]使用 SRK/HV和 PR/HV结合UNIFAC的剩余项，对170对二元体系，其中包括含甲烷或乙烷的烃类混合物体系、含复杂石蜡烃体系、含芳香烃体系、含CO2体系，进行了泡点压力和气相组成进行了计算，绝大部分偏差都在 5%以内。

Feroiu等[4]提出了HVID模型。使用SRK方程和HV混合规则结合无限稀释的UNIQUAC模型的剩余项，在较大的温度范围和压力范围内对异丙醇/水、甲醇/水、乙醇/水、丙酮/水、甲醇/苯、丙酮/甲醇六对二元体系的相平衡进行预测，得到了令人满意的结果。压力偏差和气相组成偏差基本都在5%以内。Feroiu等[5]改进了HVID模型，用UNIFAC’93代替 UNIQUAC模型的剩余项，得到 HVIDUNIFAC’93模型，并对温度范围和压力范围都较大的4种情况进行了汽液平衡预测，都得到了很好的结果：①在低压和高压、低温和高温下的对称极性体系；②含烷醇和烃类的体系；③含丙酮和烃类的体系；④烃类混合物。 HVID-UNIFAC’93混合规则还能应用于三元体系，得到令人满意的结果。

HV混合规则主要有以下缺点：①要求超额体积为零，就决定b只能使用线性混合规则；②不符合第二维里系数的边界条件；③活度系数模型都是由低压下的数据回归得到，所以HV模型不能直接使用现有的活度系数模型参数表。

2.1.2 WS混合规则

Wong和Sandler[6]提出了WS混合规则。该混合规则沿用了HV混合规则的无穷压力参考态和第一个假设，所以混合规则中的a的形式依然采用HV的形式。

但是WS混合规则比HV混合规则在两个方面有了改进。首先是考虑了AE对压力的依赖要比GE小得多，有式（7）所示的近似关系。所以采用 AE代替GE，如式（7），这样使得活度系数模型现有的参数表可用。

其次，b引入第二维里系数的形式，如式（9），这样就符合了第二维里系数的边界条件，使得 WS混合规则比HV混合规则更有理论基础。

对WS混合规则的改进主要存在于3个方面。

（1）Bij计算方法的改变 Orbey和 Sandler[7]提出ijB的新的计算形式，如式（10）。

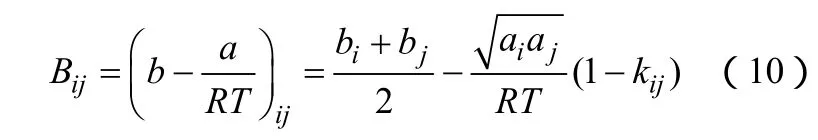
这种新的WS混合规则可以在一定的条件下转化为范德华混合规则，但是并不会降低它的汽液平衡预测和关联的能力，而且可以使用范德华混合规则长期以来积累的二元相互作用参数数据。此模型可以精确地预测复杂的二元和多元体系相平衡。

（2）kij计算方法的改进 Wong和Sandler使用在某个确定温度、中间浓度的条件下得到的汽液平衡实验数据，根据 GE模型回归得到 kij。Huang和Sandler[8]用等摩尔组成时的GE模型的值求取kij。Orbey和 Sandler[7，9]使用无限稀释活度系数下的UNIFAC模型求取 kij，这样有更全面的预测性。Eubank等[10]用第二维里系数求取kij。

（3）WS混合规则形式的改进 Ali Haghtalab和 Reza Espanani[11]将WS混合规则结合PRSV状态方程和修正的NRTL-NRF模型结合，在不同温度下，将WS混合规则的应用拓展到不同分子量的聚合物溶液的汽液平衡预测并且得到与实验数据相符合的结果。韩晓红等[12]将WS混合规则中的kij简化为只与组分和活度系数模型有关的函数。简化的WS混合规则在较宽的温度和压力范围内，与原始WS混合规则相比，精度基本相当。韩晓红等[13]考虑了 WS混合规则忽略的分子体积大小差异的影响，提出了一个改进的WS混合规则。该混合规则对16组极性-极性、非极性-极性和非极性-非极性体系的汽液平衡进行关联，比原始的WS混合规则精度有了一定的提高。吴选军等[14]以常压为参考态，提出了改进的 WS（MWS）混合规则，使用 SRK方程与MWS混合规则预测10个极性二元体系汽液平衡，结果略优于WS混合规则。Ye等[15]使用PR方程结合WS混合规则和PSRK中使用的UNIFAC模型（PRWS–UNIFAC–PSRK）、PR方程结合WS混合规则和UNIFAC-LBY模型（PRWS–UNIFAC–Lby），分别对H2O + MeOH + DME + CO2四元体系及其子体系的相平衡进行了预测。二元体系的参数能成功的拓展到三元和四元体系的汽液平衡和汽液液平衡，只是对于H2O + MeOH + DME的液液平衡结果不理想。

2.2 以零压力为参考态的GE-EoS模型

Mollerup[16]和 Heidemann、Kokal[17]等最先提出以零压力为参考态建立 GE-EoS模型的思想。但是在最初提出的模型中能量参数a隐含于V，所以要以迭代的方法得到a的值。直到1990年Michelsen等[18-20]改进了a的函数，提出了MHV1和MHV2混合规则，以零压力为参考态的 GE-EoS模型才开始广泛地应用于相平衡的计算中。MHV1和MHV2混合规则依然沿用了HV混合规则中对b使用的线性加和的方式。但是与 HV不同的是，MHV1和MHV2并不限制b必须采用线性加和的求取方式，也可以选择满足第二维里系数的混合规则。MHV1的一般形式如式（11）。

式（11）中，q0是与状态方程有关的参数。对于SRK方程，q0=−0.593。

MHV2的一般形式如式（12）。

q的值可以通过q-a方程拟合得到，这样其值依赖于所选拟合数据的适用范围。q的值也可以通过堆积率得到[21]。

Holderbaum和Gmehling[22]使用SRK方程结合UNIFAC和MHV1混合规则，但是令q0=−0.64663，得到PSRK模型。

Li等[23]改进了PSRK中结合的UNIFAC模型的一些基团参数，改进后的PSRK对非对称体系的相平衡预测结果表现良好。

零压力为参考态的 GE-EoS模型无需重新拟合活度系数模型参数，在较宽的温度和压力范围内，对极性化合物的相平衡有较好的预测结果。但是他们的预测结果和选择的活度系数模型紧密相关。

汪萍[24]分别使用PSRK、MHV2和WS混合规则计算了相同的极性物系、高压复杂体系和多元系的汽液平衡，并且对其结果作了详细的比较。结果证明，PSRK混合规则在上述所有体系中结果均能给出较小偏差，是较好的混合规则。MHV2和WS对比于PSRK混合规则均显示出了计算的局限性。MHV2和WS混合规则计算高压体系的相平衡，结果都有较大偏差。WS混合规则不适合含有惰性气体的复杂体系。

2.3 其他类型的GE-EoS模型

上述的以无穷压力和以零压力为参考态的GE-EoS模型有一个共同的缺陷，那就是都对于非对称体系的相平衡计算和预测不能得到让人满意的结果。Boukouvalas等[25]提出了LCVM混合规则，形式如式（13）。LCVM是将无穷压力下和零压力下的GE-EoS模型线性组合得到的，不满足式（1），所以它的得来基本没有理论基础，但是它在预测非对称体系相平衡方面表现得极好。

式（13）中，AV、AM和λ为LCVM混合规则的模型参数。

Boukouvalas等分别使用 MHV2、PSRK和LCVM 混合规则计算了乙烷+n-正构烷烃、二氧化碳+n-正构烷烃和甲烷+n-正构烷烃等体系的相平衡。结果表明，随着正构烷烃链长的增加，体系内物质的体积差别变大，MHV2和PSRK混合规则对相平衡的计算结果偏差快速变大。计算到n-C24时，MHV2和PSRK混合规则的偏差已经达到30%，而LCVM的偏差均在10%以内。LCVM在计算非对称性体系时展现出了非常好的结果。

LCVM 对非对称体系的相平衡有较好的结果并不是偶然的，其根本原因在于LCVM消除了状态方程组合项和活度系数模型组合项的差异[26]。

韩晓红等[27]借鉴LCVM混合规则的提出思路，将HVOS混合规则和MHV1线性组合，应用到多参数方程中。

Coniglio等[28]提出GCVM混合规则，即普遍化的LCVM型混合规则，如式（14）。

类似于LCVM的还有Orbey和Sandler[29]提出的CHV混合规则，如式（15）。

CHV混合规则使用了一个参数δ来减小对数项的贡献。CHV混合规则与LCVM有两点不同：①CHV混合规则有明确的参考压力，即无穷压力；②不像LCVM混合规则，参数λ影响超额自由能项和对数项，CHV混合规则中，参数δ只影响F-H对数项。

Jens Ahlers和 Gmehling[30]提出一个类似于PSRK的新的 GE-EoS模型。此模型基于 VTPR（volume translated Peng–Robinson）状态方程，结合UNIFAC的剩余项，对b采用非线性混合规则，对非对称体系的预测有很好的改进。其结果比Li-PSRK模型好，甚至可以和LCVM混合规则相比较。此外，对二氧化碳+乙烷体系，超额焓和超额体积的预测有很好的结果。

Tassios等[31]提出了一个普遍化的混合规则（UMR），其中 a的表达式中 GE使用原始的UNIFAC方程里组合项中的Staverman-Guggenheim项和剩余项。b使用密度依赖二次型的形式。此模型可以直接使用原始的UNIFAC的基团交互作用参数，在较大温度和压力范围内，对非对称体系的相平衡预测都能得到很好的结果。

3 结 论

GE-EoS模型通过GE将状态方程和活度系数模型联系起来，为相平衡的计算提供了新途径。从最初的HV混合规则到适用于强不对称体系的LCVM型混合规则，GE-EoS模型在适用范围和相平衡预测精度上都有了很大的提高。

根据 GE-EoS模型的提出原理和发展历程可以知道，对 GE-EoS模型的改进可以着手于以下几个方面。

（1）改进状态方程。使用能更精确描述流体P-V-T关系的状态方程，例如改进的立方型状态方程、多参数状态方程或者 SAFT型方程，会改进GE-EoS模型计算和预测相平衡的精度。

（2）改进活度系数模型的形式。例如文献[4]中提到的GE-EoS模型，只利用UNIFAC的剩余项。

（3）扩充活度系数模型的参数表。例如UNIFAC的参数一直在进行修补和增订，这必将扩大相应的GE-EoS模型的适用范围。

经过多年的发展，适用于对称体系 GE-EoS模型发展得已经较为成熟。发展针对于非对称体系的、消除组合项差异的GE-EoS模型将是新的主流。

符 号 说 明

AE—— 超额亥姆霍兹自由能，J/mol

AM，AV—— 分别为LCVM混合规则的模型参数，量纲为1

a—— 状态方程混合物的能量参数，kPa·m6·K0.5/mol2

ai，aj—— 分别为状态方程纯物质的能量参数，kPa·m6· K0.5/mol2

B —— 第二维里系数，m3/mol

Bij—— 二元交叉维里系数，m3/mol

b—— 状态方程混合物的协体积参数，m3/mol

bi，bj—— 分别为状态方程纯物质的协体积参数，m3/mol

C—— HV混合规则的模型参数，量纲为1

C0—— WS混合规则的模型参数，量纲为1

C1，C2—— 分别为GCVM混合规则的模型参数，量纲为1

C*—— CHV混合规则的模型参数，量纲为1

E—— 超额性质

FH—— Flory−Huggins模型

GE——超额吉布斯自由能，J/mol

i，j—— 组分

kij——二元相互作用参数，量纲为1

lowP——低压，kPa

M——活度系数模型

P——压力，kPa

q0——MHV1和PSRK混合规则的模型参数，量纲为1

q1，q2——分别为MHV2混合规则的模型参数，量纲为1

R——气体常数，8.314J/(mol·K)

SE—— 超额熵，J/(mol·K)

T——温度，K

UE——超额内能，J/mol

V——混合物的摩尔体积，m3/mol

Vi——纯物质的摩尔体积，m3/mol

VE——超额体积，m3/mol

x——液相摩尔分数，量纲为1

δ——CHV混合规则的模型参数，量纲为1

λ——LCVM混合规则的模型参数，量纲为1

φ——混合物的逸度系数，量纲为1

φi——纯物质的逸度系数，量纲为1

∞——无穷压力，kPa

0——零压力，kPa

[1]Chen C C，Mathias P M. Applied thermodynamics for process modeling[J]. AIChE Journal，2002，48（2）：194-200.

[2]Huron M J，Vidal. New mixing rules in simple equations of state for representing vapour-liquid equilibria of strongly non-ideal mixtures[J].Fluid Phase Equilibria，1979，3（4）：255-271.

[3]Lermite C，Vidal J. High pressure polar compounds phase equilibria calculation：Mixing rules and excess properties[J]. Fluid Phase Equilibria，1988，42：1-19.

[4]Feroiu V，Geană D. Prediction of vapor-liquid equilibria at high pressures using activity coefficients at infinite dilution[J]. Fluid Phase Equilibria，1996，120（1）：1-10.

[5]Geanã D，Feroiu V. Prediction of vapor-liquid equilibria at low and high pressures from UNIFAC activity coefficients at infinite dilution[J]. Industrial & Engineering Chemistry Research，1998，37（3）：1173-1180.

[6]Wong D S H，Sandler S I. A theoretically correct mixing rule for cubic equations of state[J]. AIChE Journal，1992，38（5）：671-680.

[7]Orbey H，Sandler S I. Reformulation of Wong-Sandler mixing rule for cubic equations of state[J]. AIChE Journal，1995，41（3）：683-690.

[8]Huang H，Sandler S I，Orbey H. Vapor-liquid equilibria of some hydrogen + hydrocarbon systems with the Wong-Sandler mixing rule[J]. Fluid Phase Equilibria，1994，96：143-153.

[9]Orbey H，Sandler S I. Modeling Vapor-Liquid Equilibria：Cubic equations of state and their mixing rules[M]. Oxford：Cambridge University Press，1998.

[10]Eubank P T，Shyu G S，Hanif N S M. New procedures for application of the Wong-Sandler mixing rules to the prediction of vapor-liquid equilibria[J]. Industrial & Engineering Chemistry Research，1995，34（1）：314-323.

[11]Haghtalab A，Espanani R. A new model and extension of Wong–Sandler mixing rule for prediction of （vapour + liquid）equilibrium of polymer solutions using EOS/GE[J]. The Journal of Chemical Thermodynamics，2004，36（10）：901-910.

[12]韩晓红，陈光明，王勤，等. 简化的 WS 混合规则在汽液相平衡中的应用[J]. 工程热物理学报，2005，26（5）：721-724.

[13]韩晓红，陈光明，王勤. 基于无穷压力为参考态的超额自由能混合规则[J]. 工程热物理学报，2006，27（6）：905-907.

[14]吴选军，张光旭，刘相鹏. SRK 方程结合超额 Gibbs 自由能规则预测汽液平衡[J]. 化学工程，2010（1）：63-66.

[15]Ye K，Freund H，Sundmacher K. Modelling (vapour + liquid) and(vapour + liquid + liquid) equilibria of {water (H2O) + methanol(MeOH) + dimethyl ether (DME) + carbon dioxide (CO2)} quaternary system using the Peng–Robinson EoS with Wong–Sandler mixing rule[J]. The Journal of Chemical Thermodynamics，2011，43（12）：2002-2014.

[16]Mollerup J. A note on the derivation of mixing rules from excess Gibbs energy models[J]. Fluid Phase Equilibria，1986，25（3）：323-327.

[17]Heidemann R A，Kokal S L. Combined excess free energy models and equations of state[J]. Fluid Phase Equilibria，1990，56：17-37.

[18]Michelsen M L. A method for incorporating excess Gibbs energy models in equations of state[J]. Fluid Phase Equilibria，1990，60（1）：47-58.

[19]Michelsen M L. A modified Huron-Vidal mixing rule for cubic equations of state[J]. Fluid Phase Equilibria，1990，60（1）：213-219.

[20]Dahl S，Michelsen M L. High-pressure vapor‐liquid equilibrium with a UNIFAC‐based equation of state[J]. AIChE Journal，1990，36（12）：1829-1836.

[21]Kontogeorgis G M，Coutsikos P. Thirty years with EoS/GEmodels：What have we learned？[J]. Industrial & Engineering Chemistry Research，2012，51（11）：4119-4142.

[22]Holderbaum T，Gmehling J. PSRK：A group contribution equation of state based on UNIFAC[J]. Fluid Phase Equilibria，1991，70（2）：251-265.

[23]Li J，Fischer K，Gmehling J. Prediction of vapor-liquid equilibria for asymmetric systems at low and high pressures with the PSRK model[J]. Fluid Phase Equilibria，1998，143（1-2）：71-82.

[24]汪萍. 立方型状态方程性能的评价研究[D]. 青岛：青岛科技大学，2004.

[25]Boukouvalas C，Spiliotis N，Coutsikos P，et al. Prediction of vapor-liquid equilibrium with the LCVM model：A linear combination of the Vidal and Michelsen mixing rules coupled with the original UNIF[J]. Fluid Phase Equilibria，1994，92：75-106.

[26]陈明君，傅杨武. EOS/GE模型预测非对称体系相平衡的进展[J].中国西部科技，2009，24（8）：5-7.

[27]韩晓红，陈光明，王勤. LCVM 型混合规则扩展用于多参数状态方程以关联混合物汽液相平衡[J]. 高校化学工程学报，2006（2）：159-163.

[28]Coniglio L，Knudsen K，Gani R. Prediction of supercritical fluid-liquid equilibria for carbon dioxide and fish oil related compounds through the equation of state—excess function (EOS-GE)approach[J]. Fluid Phase Equilibria，1996，116（1）：510-517.

[29]Orbey H，Sandler S I. Analysis of excess free energy based equations of state models[J]. AIChE Journal，1996，42（8）：2327-2334.

[30]Ahlers J，Gmehling J. Development of a universal group contribution equation of state. 2. Prediction of vapor-liquid equilibria for asymmetric systems[J]. Industrial & Engineering Chemistry Research，2002，41（14）：3489-3498.

[31]Voutsas E，Magoulas K，Tassios D. Universal mixing rule for cubic equations of state applicable to symmetric and asymmetric systems：Results with the Peng-Robinson equation of state[J]. Industrial &Engineering Chemistry Research，2004，43（19）：6238-6246.