结构用规格材抗弯强度的尺寸效应

赵 秀， 吕建雄， 江京辉， 王宏棣， 黄在华

（1.黑龙江省林业科学研究院 国家林业局制材研究重点实验室，黑龙江 哈尔滨 150081；2.中国林业科学研究院 木材工业研究所，北京 100091）

对规格材强度性质的研究表明，规格材的抗弯强度、抗拉强度以及抗压强度均会因尺寸和加载形式的变化而发生改变.规格材的强度具有尺寸效应［1］.Bohannan［2］将 Weibull脆性断裂理论用于研究尺寸和加载条件对无疵小试件抗弯强度的影响，他发现增加宽度或者长度均会引起规格材平均抗弯强度降低，只有厚度对其抗弯强度没有影响；Madsen等［3］发现规格材的抗弯性能长度尺寸效应以及抗拉性能长度和宽度尺寸效应与Buchanan的理论近似.

最弱链理论已经广泛应用于结构用木制品尺寸效应的研究中.由Weibull分布可知，在其中两种几何尺寸及加载条件确定的前提下，强度的对数与尺寸的对数呈线性相关.这种相关性已经用来确定长度、宽度及厚度的尺寸效应.

本文研究了兴安落叶松规格材抗弯强度在长宽比为18∶1时的尺寸效应因数.鉴于目前中国还未建立规格材抗弯强度的尺寸调整方法，本研究可对建立中国结构用规格材抗弯强度尺寸效应的方法提供参考，还可为木结构设计中落叶松规格材的强度设计提供指导.

1 基本理论

统计强度理论和最弱链理论多年来为传统脆性断裂研究奠定了基础.最弱链理论假定材料由许多小的单元组成，当材料中任一单元或“链”失效即认为破坏.每个“链”应力自0到σ失效的概率可以采用分布函数F（σ）来描述：

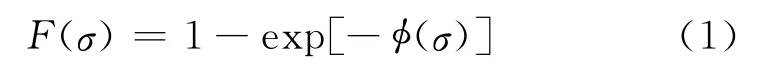
1939年，Weibull提出了一个至关重要的分布：具有极小概率的极小强度尾分布（tail distribution），该分布后来在统计学中称为 Weibull分布［4－6］.根据 Weibull分布，单位体积Vr在均匀分布的应力σ作用下，失效概率F（σ）表示为：

式中：m为 Weibull分布的尺寸参数；K为 Weibull分布的形状参数.

对于任一体积为V的试件，在均匀分布应力σ＊作用下，其失效概率为：

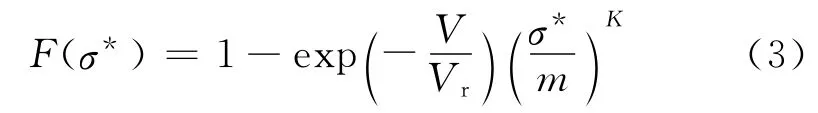
式（3）中的m和K 可以通过试验数据与Weibull分布拟合来获得.

如果材料强度变化能够用Weibull分布描述，那么，对于破坏概率相同、应力均匀分布的2个试件有如下关系：

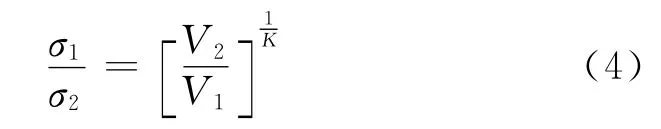
式（4）直接将强度与材料体积联系在一起，使尺寸效应得到量化.

对式（4）连续两次取对数，得到如下表达式：

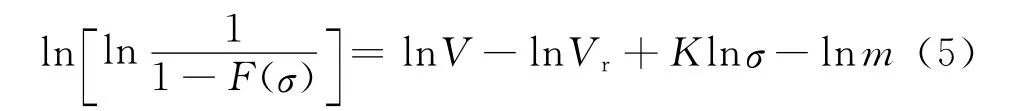
由式（5）可知，脆性材料强度的对数与尺寸的对数之间存在线性关系.

2 试验材料与方法

兴安落叶松由黑龙江省新林林业局翠岗林场和塔河林业局盘古林场采集，原木径级16～34cm，树龄35a，造材长度4.0m.制成40mm×65mm×4 000mm，40mm×90mm×4 000mm，40mm×140mm×4 000mm这3种规格材.依据GB 50005—2003《木结构设计规范》中轻型木结构用规格材的目测分级标准对兴安落叶松规格材进行目测分等，以Ⅰc，Ⅱc，Ⅲc，Ⅳc等级规格材作为本次试验材料.

本文采用 ASTM D4761－05［7］标准对规格材进行抗弯强度（MOR）测试.

MOR测试采用三分点加载形式，长宽比为18∶1.40mm×65mm×4 000mm，40mm×90mm×4 000mm，40mm×140mm×4 000mm规格材所对应的抗弯测试跨度分别为1 170mm，1 620mm，2 520mm.引起强度降等的最大缺陷的随机分布在试件测试长度内，破坏时间在1min内.试验材料的试样数见表1.

表1 试验材料的试样数Table 1 Sample number of test material

根据最弱链理论，规格材的强度与体积成反比.对于规格材这种厚度一致的材料，无需考虑其厚度尺寸效应.在载荷分布均匀，试件最终强度为σ1和σ2，纵截面的面积为A1和A2时，面积与最终强度的关系可表达为：

式中：SA为面积影响因数.

如果单独考虑试件的宽度和长度尺寸效应，则试件最终强度与试件宽度、长度的关系可表达为：

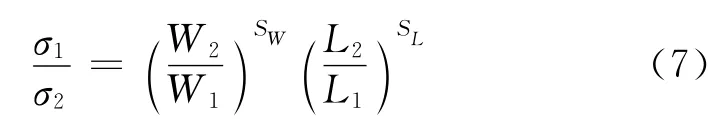
式中：W 为纵截面宽度；L为纵截面长度；SW为宽度影响因数；SL为长度影响因数.

如果宽度和长度都是单独变量，则可以通过式（7）考察宽度W 和长度L效应.对于相同长宽比（R）试件 L1＝RW1，L2＝RW2，则式（7）可表达为：

根据长宽比尺寸效应因数SR，SW和SL之间的关系：SR＝SW＋SL［8］，式（8）可表达为：

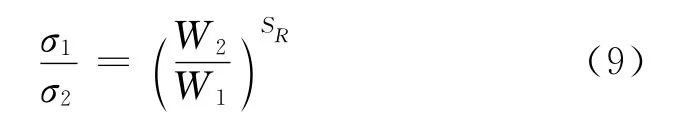
根据式（9），可通过对抗弯强度百分位值的对数及规格材宽度的对数进行回归分析，求得SR，即线性回归的斜率.采用方差分析来检验等级和强度百分位数对长宽比尺寸效应因数的影响.由于3种尺寸规格材目测等级的Ⅱc和Ⅳc等级的试样数较少，在估计其百分位值时，误差较大，因此，本文仅以3种尺寸规格材的Ⅰc和Ⅲc等级为例来计算兴安落叶松规格材抗弯强度的长宽比尺寸效应因数SR.

由于试材含水率同样影响其强度，因此在分析规格材尺寸效应因数时，应根据含水率效应，将规格材强度调整至统一含水率为15%（质量分数）后进行分析.

3 结果与讨论

本文采用非参数统计法进行估计.如果非参数估计的累积分布为Rp，则其5%分位值表示为R0.05.非参数累积分布的点估计过程如下：

（1）X1，X2，…，Xn是来自总体X 的简单随机样本，将其按从小到大的顺序排列：X（1）≤X（2）≤…≤X（n）.则称 X（1），X（2），…，X（n）为总体 X 的顺序统计量，n是样本包含的试样数.

（2）计算i，使下式成立：

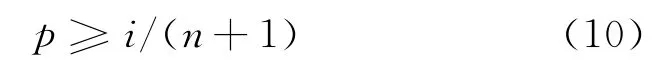
（3）j为大于或等于i的最小正整数，采用线性插值法计算p分位值如下：

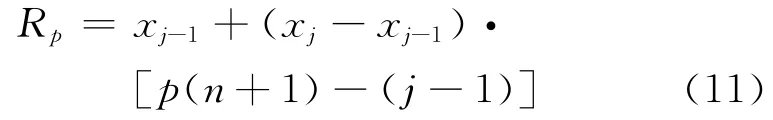
由于本试验采用一致的跨高比对3种尺寸规格材进行抗弯强度测试，根据试验数据只能得到抗弯强度的长宽比尺寸效应.首先，计算Ⅰc与Ⅲc等级的21个百分位数（0.02，0.05，0.10，0.15，…，0.90，0.95，0.98）的抗弯强度值，对于每个等级，每个百分位数均有3个强度值（3种尺寸规格材强度值的分位值）与之对应，对强度百分位值的对数及宽度的对数进行线性回归分析，直线的斜率即该点长宽比尺寸影响因数SR.Ⅰc与Ⅲc等级的21个百分位数与SR的关系见图1.图1中Ⅰc与Ⅲc等级的SR差异明显，Ⅰc等级的SR随着强度增大先略微增大后减小，在强度值最大处又明显上升；Ⅲc等级的SR整体随着强度增大呈下降趋势.Ⅰc与Ⅲc等级的SR整体变大趋势比较平缓，只是在两端极值处出现较大的波动.

对Ⅰc与Ⅲc等级的21个百分位数的SR进行方差分析，结果见表2.

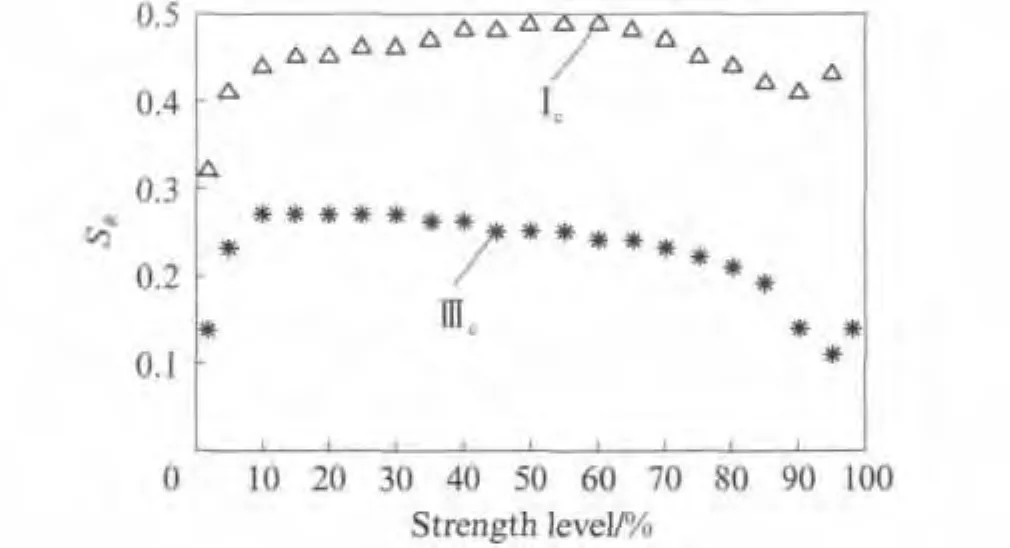
图1 Ⅰc和Ⅲc等级的SR与抗弯强度百分位数的关系Fig.1 Relation between bending size parameter SR and strength level ofⅠc，Ⅲc

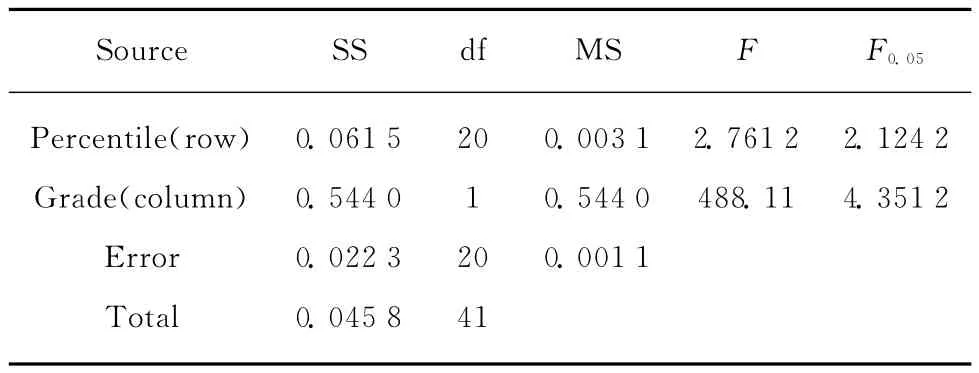
表2 Ⅰc和Ⅲc等级21个百分位数的SR的方差分析结果Table 2 Analysis of variance of SRat percentiles of gradeⅠcandⅢc

表2中F检验结果表明，在检验水平为5%时，SR在百分位数间和等级间差异显著.将对Ⅰc与Ⅲc等级的21个百分位数的SR分别进行回归分析.Ⅰc等级的SR与百分位值的回归分析结果见表3.

表3 Ⅰc等级的SR与百分位数回归分析结果Table 3 Regression analysis of size parameter SR at percentiles of gradeⅠc

表3中P＜0.05，表明回归方程显著；对斜率的t检验结果：｜t｜＜t0.05，表明斜率与零的差异不显著，即斜率为零，截距即为Ⅰc等级的SR.

Ⅲc等级的21个SR值与百分位数的回归分析结果见表4.表4的结果表明回归方程显著，t检验结果显示斜率不为零，也就是说SR不是常数，不同强度水平对应不同的SR值.由于规格材强度特征值以5%分位值为基础得到，很多标准更注重5%分位值的尺寸效应因数，本文对5%～50%分位数的10个SR值作了进一步回归分析，结果见表5.F检验的结果表明其线性关系不显著，也就是说无论在5%～50%的强度水平上还是在整体强度水平上尺寸效应因数都没有趋于常数的趋势.

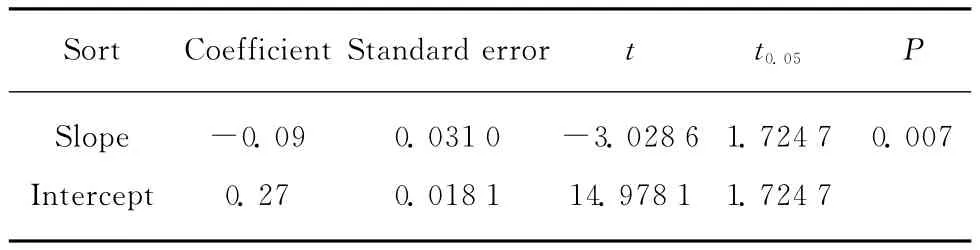
表4 Ⅲc等级的SR与百分位数回归分析结果Table 4 Regression analysis of size parameter SR at percentiles of gradeⅢc

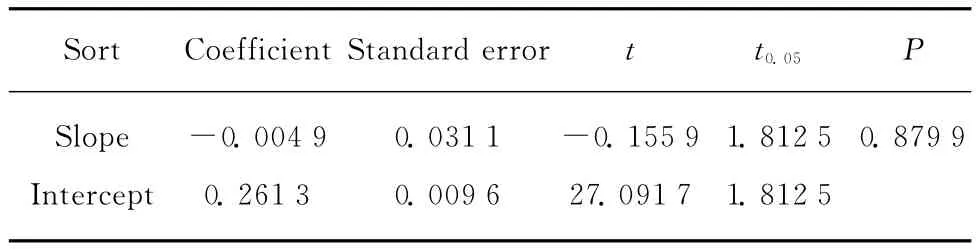
表5 Ⅲc等级的SR与百分位数（5%～50%）回归分析结果Table 5 Regression analysis of size parameter SRat percentiles（5%－50%）of gradeⅢc

根据表4结果，可将Ⅲc等级的SR与百分位数PMOR的关系表示为：

4 与北美结构用规格材抗弯强度尺寸效应因数研究结果比较

本文对Ⅰc和Ⅲc等级规格材抗弯强度的尺寸效应因数分析表明，不同等级规格材的抗弯强度长宽比尺寸效应因数SR之间存在差异.由加拿大木材协会（CWC）北美锯材分等机构（NLGA）与美国（USA）材料与测试协会合作的木材性质研究项目得到的规格材MOR尺寸效应因数及本文结果列于表6.

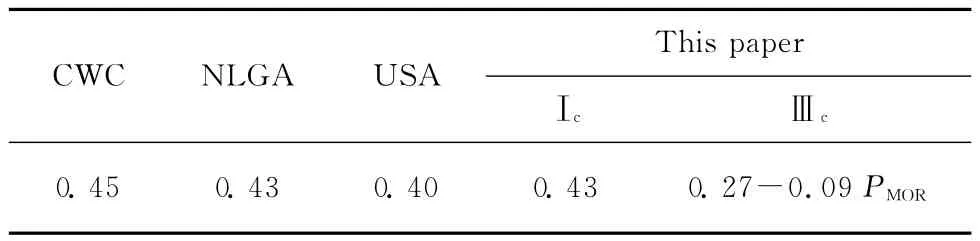
表6 北美与本文在结构用规格材尺寸效应因数上的研究结果Table 6 Results about size effect parameters of North America and this paper

加拿大木材协会与美国材料与测试协会合作的木材性质研究项目对3个树种（花旗松（pseudotsuga menziesii）、北美铁杉（tsuga canadensis）及白松（pinus strobus））的3个等级（SS，No.1，No.2）尺寸效应因数SR（抗弯强度的长／宽尺寸效应因数）进行了研究，得到SR与国际木材分等协会验证性加载测试所得SR相近，双方达成一致，将名义厚度为50cm的北美主要商品林规格材的SR近似取为0.4［2］.

本研究得到的抗弯强度Ⅰc等级的SR结果与美国和加拿大的研究结果相近，而Ⅲc等级的尺寸效应因数则明显不同.同时，加拿大木材协会与美国材料与测试协会合作的木材性质研究项目得到的结论是，等级与强度水平对规格材尺寸效应因数的影响不显著.NLGA对验证性加载测试结果的5%分位值的协方差进行分析，结果显示不同等级尺寸效应因数是一致的.Madsen等发现4种宽度尺寸规格材的SS和No.3等级抗弯强度的综合尺寸效应因数SL值不是常数［3］.Madsen［9］对铁杉（tsuga canadensis）的抗弯强度尺寸效应因数SL的研究结论为：10%分位值的SL＝0.13；50%分位值的SL＝0.19.Barrett等［1］认为将不同等级的规格材混合在一起会影响强度尺寸效应因数.从以上分析来看，研究的着重点不同，导致研究结论不同，加拿大木材协会与美国材料与测试协会更侧重于5%分位值强度的尺寸效应因数，而Madsen等是研究规格材整体强度水平的尺寸效应因数，与本文研究对象一致，得到的结论也是一致的，即规格材抗弯强度尺寸效应因数并非常数，而是受等级和强度水平影响的.

5 结论

对于抗弯强度，Ⅰc与Ⅲc等级规格材的长宽比尺寸影响因数SR整体变化趋势比较平缓，只是在两端极值处出现较大的波动；规格材等级间SR差异显著，Ⅰc等级的SR为0.43，Ⅲc等级的SR与强度百分位水平之间存在线性关系：SR＝0.27－0.09PMOR.

［1］ BARRETT J D，LAU W.Canadian lumber properties［M］.［S.l.］：Canadian Wood Council，1994：129.

［2］ BOHANNAN B.Effect of size on bending strength of wood members［R］.Madison：USDA Forest Service，1966.

［3］ MADSEN B，BUCHANAN A H.Size effect on timber explained by a modified weakest link theory［J］.Canadian Journal of Civil Engineering，1986，13（2）：218－232.

［4］ SUTHERLAND L S，SHENOI R A，LEWIS S M.Size and scale effects in composites：I.Literature review［J］.Composites Science and Technology，1999，59（2）：209－220.

［5］ BAZANT Z P，CHEN Erping.Scaling of structural failure［J］.Applied Mechanics Reviews，1997，50（10）：593－627.

［6］ WISNOM M R.Size effects in the testing of fiber－composite materials［J］.Composites Science and Technology，1999，59（13）：1937－1957.

［7］ ASTM D4761－05 Standard test methods for mechanical properties of lumber and wood－base structual material［S］.

［8］ BARRETT J D，FEWELL A R.Size factors for the bending and tension strength of structural lumber［R］.Lisbon：Proceedings CIB Working Commission，1990.

［9］ MADSEN B.Structural behavior of timber［M］.North Vancouver：Timber Engineering Ltd，1992：137－153.