高韧性PVA－FRCC单轴受压力学性能及本构关系

李 艳， 刘泽军

（河南理工大学 土木工程学院，河南 焦作 454003）

高韧性聚乙烯醇（PVA）纤维增强水泥基复合材料（PVA－FRCC）是一种由水泥基体与短纤维组成的复合材料，它具有很大的延展性，在直接拉伸荷载作用下表现出多裂缝开裂与应变硬化特性［1－3］，具有较强的能量吸收能力，可显著改善混凝土结构的抗震性能与抗剪性能［4－5］.

我国目前正处于大规模基础工程建设时期，大部分地区位于地震区，其基础工程需要进行抗震设防和延长服役年限，需要大量的高性能建筑材料.为使高韧性PVA－FRCC在实际工程中推广应用，就需对其强度和变形特性进行系统研究.本文通过高韧性PVA－FRCC单轴受压试验，研究了粉煤灰、硅灰掺量（质量分数）及PVA纤维掺量（φf，体积分数）对其单轴受压力学性能的影响，建立了单轴受压本构关系，以期为今后进行高韧性PVA－FRCC结构或构件设计计算提供理论依据.

1 试验概述

1.1 试验原材料

P·O 42.5水泥；Ⅰ级粉煤灰；硅灰；最大粒径为1.18mm的天然河砂；FDN高效减水剂；北京中纺纤建科技有限公司生产的PVA纤维，其性能指标见表1.

表1 PVA纤维性能指标Table 1 Properties of PVA fiber

1.2 试验配合比

采用大掺量粉煤灰替代水泥来制备高韧性PVA－FRCC，配合比见表2.为提高试件强度，在满足韧性的前提下采用了较低的水胶比，其水胶比（质量比）为0.23，砂胶比（质量比）为0.36.

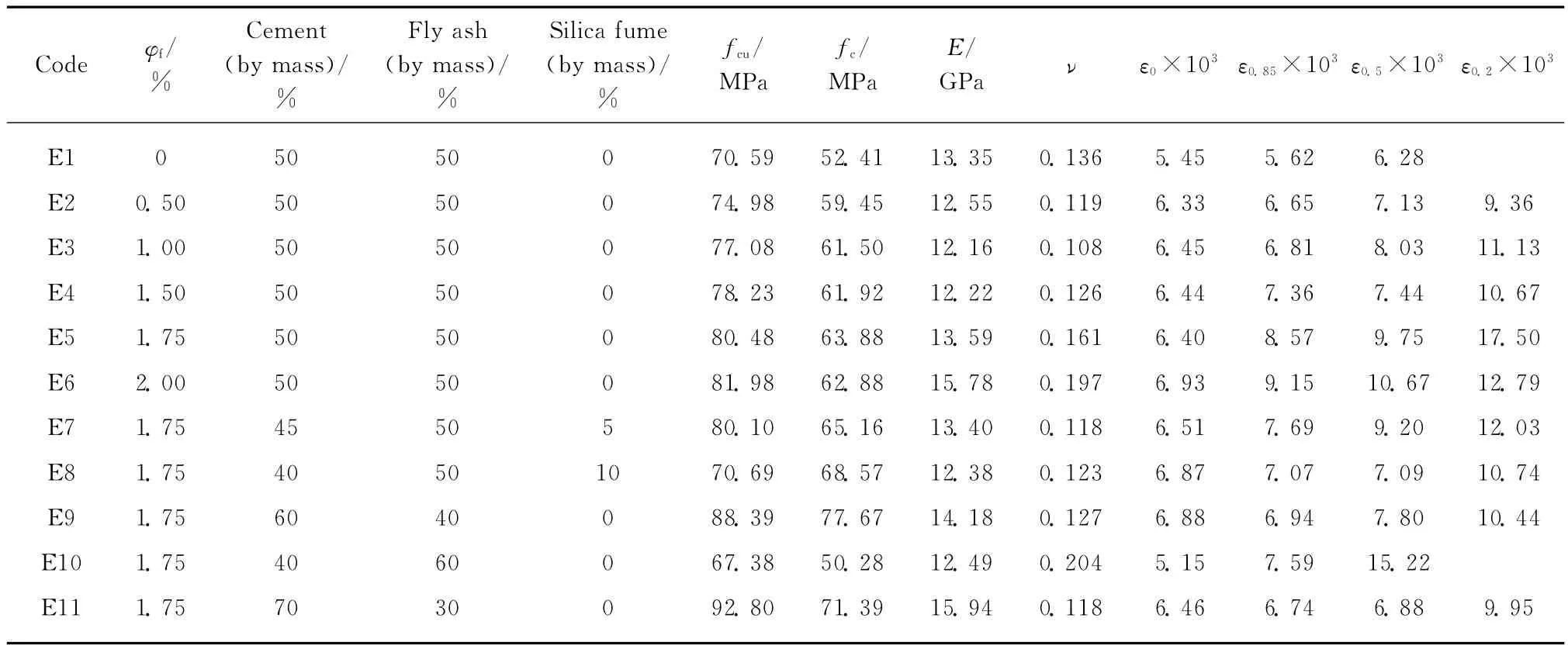
表2 试验配合比设计与试验结果Table 2 Mix design for experimental program and test result

1.3 试件制备和试验方法

试验使用的PVA纤维具有亲水性，在搅拌过程中分散性较好，故采用纤维后掺法.先将胶凝材料和细砂混合干拌2min，然后将减水剂溶入水中后加入到拌和物中搅拌2～5min，人工加入PVA纤维，搅拌4～5min，浇筑、振捣、夯实，成型24h后拆模，标准养护28d.

立方体抗压强度试件尺寸为40mm×40mm×160mm，每组试件3个.抗折强度试验设备为DKZ－5000电动抗折试验机，抗压强度试验设备为JYE－300A型全自动恒应力压力试验机.单轴抗压试验采用φ75×150mm圆柱体试件，试验设备为RMT－150B型伺服试验机，以试件轴向变形控制加载，单轴压缩速率为0.01mm／s，分别采用5.0mm 和2.5mm位移传感器测量试件轴向变形和横向变形，采用1 000kN的力传感器测量轴向荷载.每组圆柱体试件6个，试验时先用3个试件测定单轴抗压应力－应变曲线，然后取轴心抗压强度的40%作为弹性模量试验的控制荷载，以相同的速度反复加、卸载8次，最后加载直至试件破坏.

2 试验结果与分析评价

高韧性PVA－FRCC的立方体抗压强度fcu，轴心抗压强度fc，弹性模量E，泊松比ν及各组应力－应变曲线特征点处的实测应变试验结果如表2所示.

2.1 抗压强度

在砂浆基体中加入PVA纤维可提高其韧性.但PVA纤维掺量对抗压强度的影响有限，从表2可以看出，在基体强度一定时，随着PVA纤维掺量的增加，高韧性PVA－FRCC的立方体抗压强度和轴心抗压强度均提高，但提高幅度有限，当PVA纤维掺量从0%增加到2.0%时，立方体抗压强度提高了16.1%，轴心抗压强度提高了20.0%.利用线性回归分析得到fcu与φf的关系如图1所示，其表达式为：

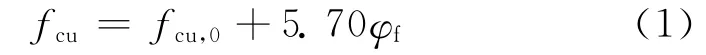
式中：fcu，0为PVA纤维掺量0%时高韧性PVAFRCC的基体强度.

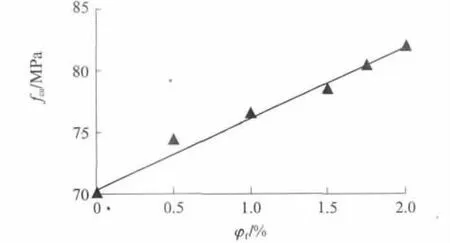
图1 fcu与φf的关系Fig.1 Relationship between cubic compressive strength and volume ratio of PVA fiber

用粉煤灰、硅灰等矿物掺合料替代水泥后可降低混凝土水化热，提高密实度，从而大大提高其耐久性［6－7］.表2显示，大掺量粉煤灰替代水泥降低了高韧性PVA－FRCC的抗压强度，当粉煤灰掺量从胶凝材料质量的30%增加到60%时，立方体抗压强度降低了37.7%，轴心抗压强度降低了40.8%，可见粉煤灰掺量对高韧性PVA－FRCC抗压强度的影响较大.对于大掺量粉煤灰高韧性PVA－FRCC而言，0%～10%硅灰掺量对其抗压强度的影响并不明显.

根据表2中fcu与fc的试验结果，可得二者的关系为：

高韧性PVA－FRCC的fc／fcu与高强度混凝土（fc／fcu＝0.83［8］）及钢纤维混凝土（fc／fcu＝0.81［9］）较接近.

2.2 静力受压弹性模量和泊松比

高韧性PVA－FRCC基体中不包含粗骨料，而且为保证其受拉应变－硬化效应的充分发挥，还限制了基体中砂子的粒径和含量.本试验砂子的最大粒径为1.18mm，砂胶比较小（0.36），因而所测弹性模量比普通混凝土的弹性模量低.从表2还可以看出，弹性模量随着抗压强度的提高而增加；PVA纤维掺量对弹性模量也有影响，但影响不大.当抗压强度大致相同时，由于PVA纤维的掺入使基体孔隙率增大，匀质性降低，微裂缝增多，导致高韧性PVA－FRCC的弹性模量降低，这与文献［10］的结论一致.

弹性模量E与fcu的关系如图2所示，其表达式为：

图2 E与fcu的关系Fig.2 Relationship between elasticity modulus and cubic compressive strength

从表2可以看出，PVA纤维掺量对高韧性PVA－FRCC的泊松比没有明显影响.

2.3 电镜分析

为探讨PVA纤维、粉煤灰及硅灰掺量对高韧性PVA－FRCC压缩韧性影响的原因，对单轴受压破坏后的试件进行了电镜分析，如图3所示.由图3（a）可见，许多未水化的粉煤灰球形颗粒在基体中可有效改善PVA纤维和高韧性PVA－FRCC基体的界面黏结力.当压应力超过峰值应力后，应力－应变曲线下降，裂缝不断扩展，PVA纤维沿着裂缝被逐渐拔出，从而起到了阻裂作用，提高了试件的压缩韧性.由图3（b）可见，掺入10%（质量分数）的硅灰后，基体的密实度增加，这对PVA纤维的阻裂作用不利.图3（c）显示，PVA纤维从大掺量粉煤灰的基体中被拔出后，界面较为光滑.图3（d）显示，被拔出后的PVA纤维表面损伤较小.

2.4 受压应力－应变曲线

试件的应力－应变曲线如图4所示.由图4可以看出，在加载初期，应力－应变曲线明显下凹，这是由于试件端部不平整或在单轴压缩加载初期，试件内部的初始微裂缝呈现闭合所致［11］.随后，应力和应变基本保持线弹性关系.当应力达到抗压强度的80%左右时，由于内部裂缝扩展，应变增长速度大于应力增长速度，使应力－应变关系呈曲线形变化.当应力达到峰值应力时，试件表面出现细小的裂缝，这时PVA纤维的阻裂作用不明显.峰值应力后，曲线下降，裂缝不断扩展，PVA纤维的阻裂作用明显，使应力下降缓慢，在反弯点时，应力下降率达到最大值.过反弯点后，试件表面出现斜裂缝，PVA纤维沿着裂缝被逐渐拔出.可见，PVA纤维可有效增大高韧性PVA－FRCC的塑性变形能力，且随着掺量的增加，其压缩韧性明显改善（见图4（a））.图4（b）显示，掺入硅灰后，应力－应变曲线下降段陡峭，压缩韧性降低.图4（c）显示，在PVA纤维掺量一定时，随着粉煤灰掺量的增加，高韧性PVA－FRCC的峰后延性增加.

图3 试件的电镜照片Fig.3 SEM photos of specimens

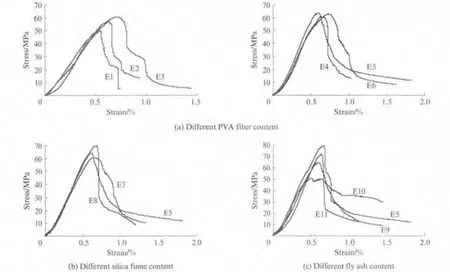
图4 高韧性PVA－FRCC的受压应力－应变曲线Fig.4 Compressive stress－strain curves of PVA－FRCC with high toughness

从表2可以看出，高韧性PVA－FRCC的峰值应变为5.15×10－3～6.93×10－3，明显大于普通混凝土的峰值应变（2.00×10－3），而且应变很大时仍具有一定的残余强度.对乱向分布的高韧性PVAFRCC，当基体组分大致相同时，其应力－应变曲线特征主要受PVA纤维掺量影响，利用线性回归分析得到峰值应变ε0与φf的关系如图5所示，其表达式为：

式中：ε0，0为 PVA 纤维掺量0%时高韧性 PVAFRCC基体的峰值应变.

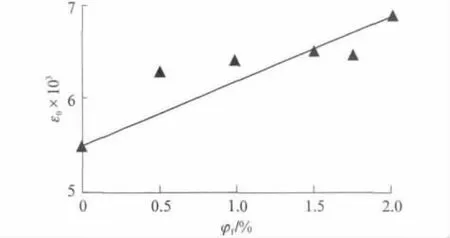
图5 ε0与φf的关系Fig.5 Relationship between peak strain and volume ratio of PVA fiber

根据表2中的数据，可得ε0.85，ε0.5，ε0.2的平均值分别为7.46×10－3，8.92×10－3，11.62×10－3.表2显示，随着PVA纤维掺量的增加，应力－应变曲线下降段各特征点的应变均有增加的趋势，这充分说明PVA纤维可明显改善高韧性PVA－FRCC的压缩韧性；掺入硅灰后，应力－应变曲线下降段各特征点的应变降低，压缩韧性降低；粉煤灰可改善PVA纤维与高韧性PVA－FRCC基体的界面黏结力，提高试件的压缩韧性，因而随着粉煤灰掺量的增加，应力－应变曲线下降段各特征点的应变增大.

3 单轴受压本构方程的建立

将各组试件实测的应力－应变曲线采用无量纲坐标表示，令x＝ε／ε0，y＝σ／σ0.根据曲线特点并参考文献［8］，应力－应变曲线应满足以下条件：（1）当x＝0时，y＝0；（2）0≤x＜1，＜0；（3）x＝1时，y＝1，＝0；（4）在＝0处，xD＞1.0；（5）在＝0处，xE（≥ xD）是下降段曲线上曲率最大点；（6）当x→∞时，y→0→0；（7）x≥0时，0≤y≤1.

基于高韧性PVA－FRCC应力－应变曲线的特点，参考文献［12］，可采用如下模型表征：

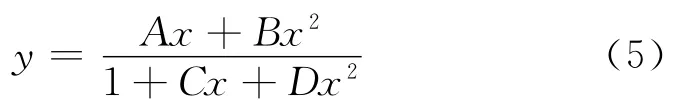
式中：A，B，C，D 为待定参数.

3.1 应力－应变曲线上升段（0≤x≤1）

由条件（3）及式（5）可得：

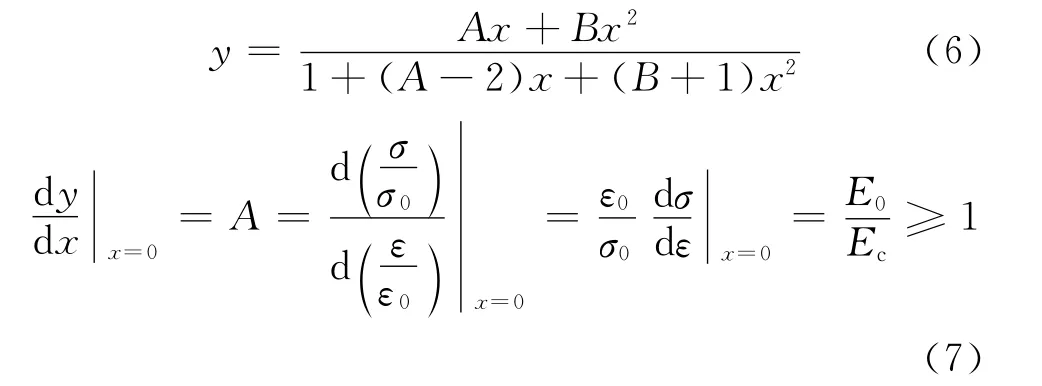
可见，待定参数A为初始切线模量E0与峰值应力点处割线模量Ec的比值.当A＝1时，应力－应变曲线上升段变为直线，即呈线弹性.

对式（6）求二阶导数，且当x＝0，A＝1时，应力－应变曲线上升段为直线段，得：

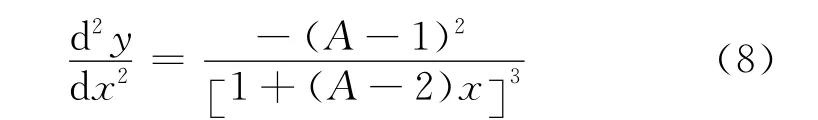
对于∀x（0≤x＜1），∀A（A≥1），上式恒小于0，满足条件（2），故上升段应力－应变曲线可表示为：

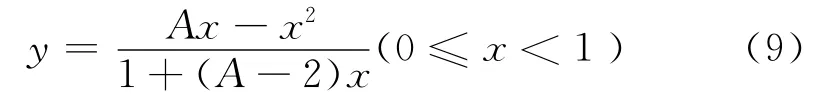
式（9）显然满足条件（7）.

3.2 应力－应变曲线下降段（x≥1）

应力－应变曲线的下降段模型仍采用式（5）表示，但待定参数 A，B，C，D 应改为 A1，B1，C1，D1，即：

由条件（6），（3）及式（10）可得：

式（11）显然满足条件（4），（5），（6）和（7），故式（11）可作为PVA－FRCC应力－应变曲线下降段方程.

3.3 本构方程参数的确定

依据最小二乘法，对高韧性PVA－FRCC应力－应变曲线进行非线性回归，得到A，A1及其相关系数如表3所示.A越大，峰值应力与弹性极限应力的差值越大，A1越大，应力－应变曲线下降段越平缓.从表3可以看出，随着PVA纤维掺量的增加，A，A1均增大.试件E6的A1小于试件E5，这是由于PVA纤维的分散性不好，使试件E6的实测应力－应变曲线下降段略显陡峭.A和A1可反映PVA纤维掺量对高韧性PVA－FRCC强度及压缩韧性的影响.由于硅灰的掺入降低了高韧性PVA－FRCC的压缩韧性，因而A1减小；随着粉煤灰掺量的增加，A，A1均增大，因此A和A1也可反映大掺量粉煤灰对高韧性PVA－FRCC强度和压缩韧性的影响.

表3 高韧性PVA－FRCC应力－应变曲线参数Table 3 Parameters on stress－strain curves of PVA－FRCC with high toughness

由表3可见，高韧性PVA－FRCC应力－应变曲线A的拟合值相关性很好，而A1的拟合值相关性较差，这主要是由于曲线下降段受试验方法和试验设备的影响较大.此外A1体现了高韧性PVAFRCC应力－应变曲线峰后压缩韧性的大小，受各种因素的影响较大.根据试验数据，各组应力－应变曲线上升段的A相差不大，故可将A取为各组试验值的平均值1.101，这时应力－应变曲线下降段的A1可表示为：

各组实测应力－应变曲线与本构方程对比曲线如图6所示.由图6可见，试验曲线与拟合曲线总体上吻合较好.

图6 实测应力－应变曲线与本构模型比较示例Fig.6 Example of comparison between stress－strain curve and constitutive model

4 结论

（1）PVA纤维的阻裂增强效果与其分散性息息相关，当基体强度一定、纤维分散良好、PVA纤维掺量不超过2%时，随着PVA纤维掺量的增加，高韧性PVA－FRCC的立方体抗压强度和轴心抗压强度均提高，但提高幅度有限.大掺量粉煤灰替代水泥降低了高韧性PVA－FRCC的抗压强度，0%～10%的硅灰掺量对其抗压强度的影响并不明显.

（2）高韧性PVA－FRCC的弹性模量随抗压强度提高而增加，当高韧性PVA－FRCC抗压强度大致相同时，PVA纤维的掺入使其弹性模量降低.通过分析分别得到了轴心抗压强度fc和弹性模量E与立方体抗压强度fcu的关系.

（3）PVA纤维可有效提高高韧性PVA－FRCC基体的塑性变形能力，且随着纤维掺量的增加，其压缩韧性明显改善.在PVA纤维掺量一定时，随着粉煤灰掺量的增加，峰值后的延性增加，但是，硅灰的掺入则降低了压缩韧性.

（4）基于实测的高韧性PVA－FRCC应力－应变曲线，提出了高韧性PVA－FRCC单轴受压本构方程，为高韧性PVA－FRCC结构非线性有限元分析及结构设计提供了理论依据.

［1］ TOSUN－FELEKOGˇLU K，FELEKOGˇLU B，RANADE R，et al.The role of flaw size and fiber distribution on tensile ductility of PVA－ECC［J］.Composites Part B：Engineering，2014，56（1）：536－545.

［2］ 李贺东.超高韧性水泥基复合材料试验研究［D］.大连：大连理工大学，2008.LI Hedong.Experimental research on ultra high toughness cementitious Composites［D］.Dalian：Dalian University of Technology，2008.（in Chinese）

［3］ LI M，LI V C.High－early－strength ECC for rapid durable repair—Material properties［J］.ACI Materials J，2011，108（1）：3－12.

［4］ LI V C.高延性纤维增强水泥基复合材料的研究进展及应用［J］.硅酸盐学报，2007，35（4）：531－536.LI V C.Progress and application of engineered cementitious composites［J］.Journal of the Chinese Ceramic Society，2007，35（4）：531－536.（in Chinese）

［5］ KABELE P，KANAKUBO T.Experimental and numerical investigation of shear behavior of PVA－ECC in structural elements［C］∥Fifth International RILEM Workshop on High Performance Fiber Reinforced Cement Composites（HPFRCC 5）.Mainz：［s.n.］，2007：137－146.

［6］ MARTINOLA G，BAEUML M F，WITTMANN F H.Modified ECC by means of internal impregnation［J］.Journal of Advanced Concrete Technology，2004，12（2）：207－212.

［7］ LI V C，LEPECH M，WANG S，et al.Development of greenECC for sustainable infrastructure systems［C］∥International Workshop on Sustainable Development and Concrete Technology.Beijing：Iowa State Univ，2004：81－192.

［8］ 过镇海.混凝土的强度和变形—试验基础和本构关系［M］.北京：清华大学出版社，1997：31－32.GUO zhenhai.Strength and deformation of concrete—Experimental basis and constitutive relation［M］.Beijing：Tsinghua University Press，1997：31－32.（in Chinese）

［9］ 曾志兴.钢纤维轻骨料混凝土力学性能的试验研究及损伤断裂分析［D］.天津：天津大学，2002.ZENG Zhixing.Experimental study on mechanical properties of steel fiber reinforced lightweight aggregate concrete and analyse on damage and fracture［D］.Tianjin：Tianjin University，2002.（in Chinese）

［10］ 徐世烺，蔡向荣，张英华.超高韧性水泥基复合材料单轴受压应力应变全曲线试验测定与分析［J］.土木工程学报，2009，42（11）：79－85.XU Shilang CAI Xiangrong，ZHANG Yinghua.Experimental measurement and analysis of the axial compressive stressstrain curve of ultra high toughness cementitious composites［J］.China Civil Engineering Journal，2009，42（11）：79－85.（in Chinese）

［11］ 尤明庆.岩石的力学性质［M］.北京：地质出版社，2007：230－231.YOU Mingqing.Mechanical properties of rock［M］.Beijing：Geological Book Company，2007：230－231.（in Chinese）

［12］ 高丹盈，刘建秀.钢纤维混凝土基本理论［M］.北京：科学技术文献出版社，1994：320－321.GAO Danying，LIU Jianxiu.Fundamental theory of steel fiber reinforced concrete［M］.Beijing：Science and Technology Literature Press，1994：320－321.（in Chinese）