基于观测器的LMI振动控制算法

王露健，周星德，秦飞马，张 翔，李勇直

(河海大学土木与交通学院，江苏南京 210098)

振动主动控制中的系统模型只是实际物理系统的一个近似，模型误差存在必然会降低控制系统的功能;由于系统的状态不可测或不易观测，测量结果可能受噪声干扰，必须采用观测器来进行状态变量估计［1-3］。基于观测器的状态变量估计是振动主动控制技术应用于实际的关键，而观测变量个数往往少于状态变量个数，导致状态变量估计值出现较大误差。为了实现振动主动控制的目的，控制器设计需满足稳定性要求。目前，多数控制器设计利用Lyapunov稳定性原理来保证闭环系统的稳定性［4-5］。此外，控制器设计还要满足一定的性能指标及约束条件。随着振动控制策略研究的深入，设计中往往存在多个约束条件，同时各个约束条件之间相互制约，因而线性矩阵不等式(LMI)得到了应用［6-11］。但在实际的应用过程中，含多个未知参数的LMI求解存在缺陷，因此，笔者以文献［12］作为参考对基准建筑物进行控制器设计，并对由约束条件及性能指标构造的含2个未知参数的LMI求解做出改进。

1 控制器设计

建立状态方程如下:

式中:xp——2r×1维状态矢量;t——时间变量;A——2r×2r维矩阵;D——2r×g 维矩阵;u——作动器控制力向量;E——2r×1维矩阵——地震波加速度。

以位移作为控制输出矢量:

式中:H——q×2r维输出矩阵(q为控制输出的状态变量数目)。

采用Kalman滤波器进行状态变量估计，设测量方程与控制输出方程一致，最优估计如下:

其中

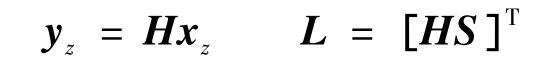
由于地震波是未知的，在进行控制器设计时采用不考虑地震外激励的模式。误差函数定义为

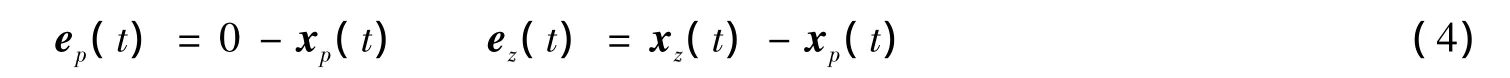
其导数为

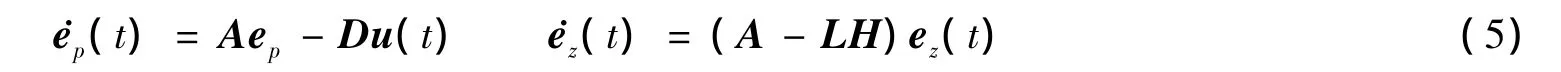
对照文献［12］，本文不存在参考模型，故将控制力的表达式定义为

式中:γ——正数;P——相应维数的正定矩阵。

为保证控制力作用下系统的稳定性，构建Lyapunov函数

对其求导，简记为如下二次型形式:

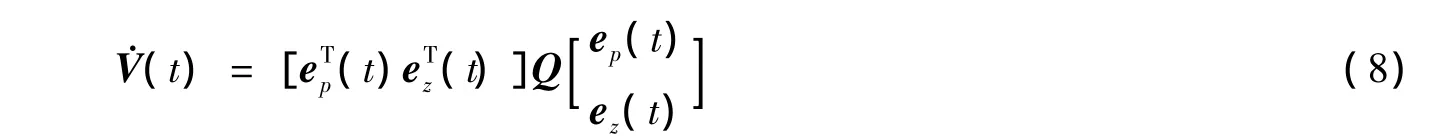
其中

Basher［12］提出基于观测器的LMI控制方法，要求矩阵Q＜0，满足稳定性，但未给出P和γ的确定方法。同时确定P和γ是很困难的，此外，考虑到‖P‖和γ的数量级问题，本文提出如下优化模型:

在求解策略方面，提出通过给定P来优化γ的方案;为了保证‖P‖和γ数量级一致，可以对角矩阵的方式给出初值P;笔者通过调试，发现采用单位矩阵作为初值P是一个较优的选择。具体求解过程如下:(a)令P=I(I为相应维数的单位矩阵);(b)通过式(9)进行优化计算，确定目标函数J;(c)利用式(6)确定控制力，在进行仿真分析时，笔者发现u=γDTPxz不能达到很好的控制效果，进而根据实际控制要求来确定调节因子β。最终得到控制力的表达式为

2 实例分析

有关3层基准建筑物的详细定义、截面尺寸及节点划分可参阅文献［13］。

每个节点考虑水平、竖直和转动共3个自由度，整个结构共计60个自由度，去掉约束后还有45个自由度。在地震作用下的振动方程可表示为

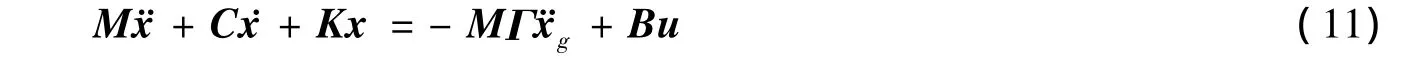
式中:M、C、K——建筑物质量、阻尼和刚度矩阵，均为45×45阶矩阵;Γ——地震作用的位置矩阵;¨xg——地震波加速度;B——作动器定位矩阵，为45×p阶矩阵;u——p×1维控制力矢量(p为作动器数目)［14］。

为了验证本文方法的可行性，对3层基准建筑物进行仿真。地震波采用Kobe波，时间历程取为50 s。楼层1布置2个相同的作动器，楼层2和楼层3各布置1个作动器。控制输出楼层2和楼层3的位移。

由于3层基准建筑物的自由度数目比较多，本例中取前5阶模态进行降阶计算［15-16］。前5阶自然频率为0.99 Hz、3.06 Hz、5.83 Hz、7.23 Hz、9.97 Hz。

式(1)的状态方程中xp为10×1维状态矢量，A、D、E分别为10×10、10×2、10×1维矩阵。式(2)中H为2 ×10 维输出矩阵，其中 H(1，2)=1，H(2，3)=1，其余均为0。

通过求解器，得到Kalman滤波器的增益矩阵L，从而得到所有状态变量的估计值。

再通过优化模型(式(9))的求解，得到J=0.7。然后经过反复调试，得到较优的调节因子β=1013，从而得到最终的控制律α:

最后给出控制前后楼层2和楼层3的位移响应及作动器控制力的时程曲线，见图1、图2。

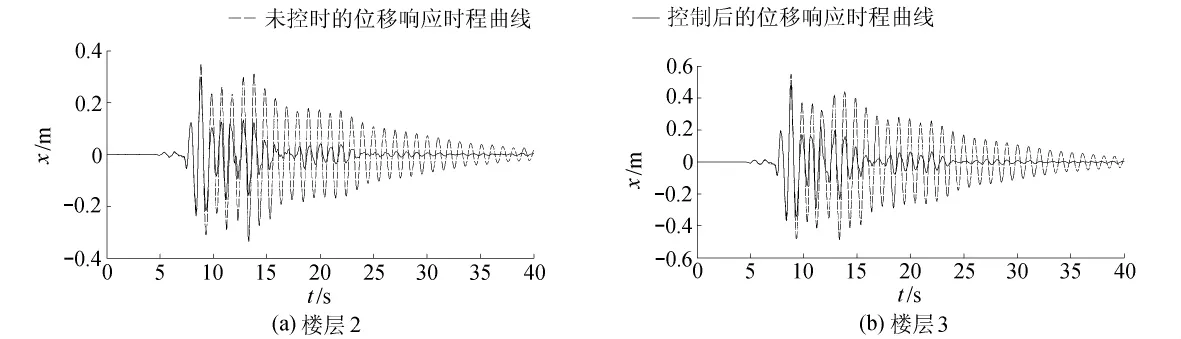
图1 控制前后的位移时程曲线Fig.1 Displacement time histories before and after control

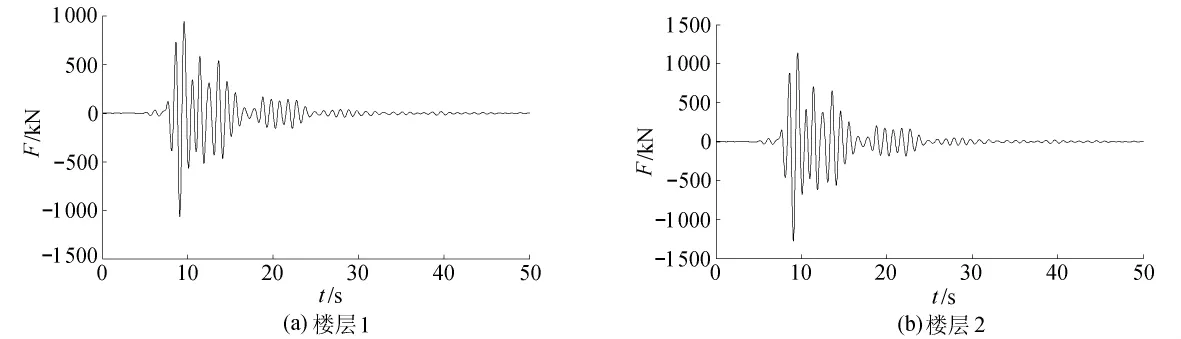
图2 作动器控制力时程曲线Fig.2 Control time histories of actuator

3 结 语

以3层基准建筑物为研究对象，在保证系统稳定并满足约束条件的限制下，建立了含有2个未知参数的线性矩阵不等式，通过对不等式求解，得到较优的性能指标，并在不断的调试下得到最终的控制律。从仿真结果看，本文方法具有较好的控制效果。

［1］GONZALEZ R，FIACCHINI M，RODRIGUEZ F，et al.Adaptive control for a mobile robot under slip conditions using an LMI-based approach ［J］.European Journal of Control，2010，16(2):144-155.

［2］KARIMI H R.Observer-based mixed H2/H∞control design for linear systems with time-varying delays:an LMI approach［J］.International Journal of Control Automation and Systems，2008，6(1):1-14.

［3］韦俊青.基于状态观测器的不确定性线性系统鲁棒控制研究［D］.广州:广东工业大学，2013.

［4］SATHANANTHAN S，KNAP M J，STRONG A，et al.Robust stability and stabilization of a class of nonlinear discrete time stochastic systems:an LMI approach［J］.Applied Mathematics and Computation，2012，219(4):1988-1997.

［5］YANG Xikai.Observer-based anti-windup compensator design for saturated control systems using an LMI approach［J］.Computer＆ Mathematics with Applications，2012，64(5):747-758.

［6］ZHANG Qingjiang，YE Sijun.An enhanced LMI approach for mixed H-2/H-infinity flight tracking control［J］.Chinese Journal of Aeronautics，2011，24(3):324-328.

［7］ZHANG Kuanyu.Multi-objective control for stochastic model reference systems based on LMI approach and sliding mode control concept［J］.International Journal of Systems Science，2013，44(4):739-749.

［8］李文章，吴凌尧，郭雷.基于LMI的结构振动鲁棒H∞控制［J］.振动工程学报，2008，21(2):157-161.(LI Wenzhang，WU Lingyao，GUO Lei.Robust H∞ control of structural vibration based on LMI［J］.Journal of Vibration Engineering，2008，21(2):157-161.(in Chinese))

［9］KARIMI H R，GAO Huijun.LMI-based H-infinity synchronization of second-order neutral master-slave systems using delayed output feedback control［J］.International Journal of Control Automation and Systems，2009，7(3):371-380.

［10］BAI Mingchang.Robust control of uncertain time-delay systems via sliding mode control and LMI-H(infinity)technique［J］.Journal of Marine Science and Technology-Taiwan，2008，16(1):1-7.

［11］LIAN Changhua，YU Kewei.LMI optimization approach on robustness and H-infinity control analysis for observer-based control of uncertain systems［J］.Solitons ＆ Fractals，2008，36(3):617-627.

［12］BASHER H A.An LMI approach for observer based model reference control［C］//IEEE SoutheastCon-Proceedings.Jacksonville，FL:IEEE Jacksonville Sect，2013:1-5.

［13］OHTORI Y，CHRISTENSON R E，SPENCER B F，et al.Benchmark control problems for seismically excited nonlinear buildings［J］.Engineering Mechanics，2004，130(4):366-385.

［14］周星德，陈国荣.3层基准建筑物地震激励多目标控制［J］.振动工程学报，2006，19(3):394-398.(ZHOU Xingde，CHEN Guorong.Multiobjective control for earthquak-excited 3-storey benchmark buildings［J］.Journal of Vibration Engineering，2006，19(3):394-398.(in Chinese))

［15］周星德，姜冬菊.结构振动主动控制［M］.北京:科学出版社，2009.

［16］蒋杨，周星德，王玉，等.基于分数阶的建筑结构预测控制方法［J］.河海大学学报:自然科学版，2011，39(5):556-560.(JIANG Yang，ZHOU Xingde，WANG Yu，et al.Predictive control method of building structure based on fractional order［J］.Journal of Hohai University:Natural Sciences，2011，39(5):556-560.(in Chinese))