12 kV真空灭弧室内部电场数值计算与分析
2014-10-11张洪达
孙 巍,于 琪,刘 洋,张洪达,孙 晨
(1.黑龙江省电力科学研究院,哈尔滨 150030;2.哈尔滨供电公司客服服务中心,哈尔滨 150030)
目前,真空断路器在中压配电系统中已经占据绝对的优势,真空灭弧室设计对真空灭弧室内部绝缘性能的要求越来越高[1-3]。灭弧室内部的电场分布对真空灭弧室的开断和绝缘性能具有决定性的影响。如果电场分布不均匀,则触头间隙将会击穿,最终导致开断失败或绝缘故障,如何使真空灭弧室内部的电场合理分布,则成为重要的研究课题。
动、静触头之间的开距关系着触头间是否发生绝缘击穿,从而直接影响了真空灭弧室的绝缘性能;真空灭弧室内部的绝缘性能又与触头和屏蔽罩等部件的结构和尺寸关系很大。对此,本文采用ANSYS有限元分析软件,运用有限元分析方法,对中压真空灭弧室内部电场进行仿真研究,并在仿真结果的基础上,改变真空灭弧室中动、静触头之间的开距、触头和悬浮屏蔽罩的形状等因素,以确定不同因素对真空灭弧室内部电场分布的影响,从而使中压真空灭弧室的绝缘性能得到改善。
1 电场仿真模型的建立
假设在整个中压真空灭弧室内部电场的计算区域内没有分布自由电荷,满足Laplace方程,Laplace方程为
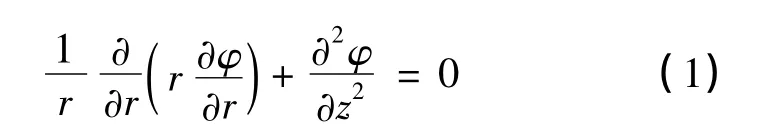
边界条件为
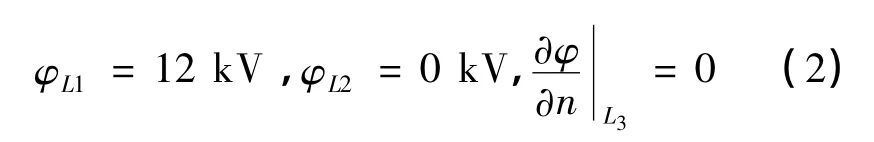
式中:φ为电位;L1为静触头边界;L2为动触头边界;L3为中轴线和无限远边界。
伽辽金法得出电势弱解方程为

式中,s是由 L1、L2、L3围成的封闭区域。
求解上述有限元方程得到各节点的电位,再由E=-gradφ公式便可得到相应的电场强度[4]。
真空灭弧室中的悬浮屏蔽罩所满足的方程为

式中:φ、S和Q分别为悬浮屏蔽罩的电位、表面积和所带的电荷量。
中压真空灭弧室内部电场的计算模型如图1所示。为确保计算结果的准确性,建立的计算模型和灭弧室样品均按照1∶1的比例建立,触头之间的开距按照额定值8 mm进行设定。
模型由屏蔽罩、静导电杆、动导电杆、触头座、触头支撑和触头片几部分构成。其中:屏蔽罩的长度为138 mm,外径为102.5 mm;触头片的直径为79 mm,触头片的厚度为5 mm,触头片上的径向直槽的宽度为2 mm,长度为22 mm;触头座的高度为22 mm,杯壁厚度为9 mm,触头座的杯指与水平面的夹角为25°。

图1 中压真空灭弧室内部电场的计算模型Fig 1 Calculation model of electric field inside medium voltage vacuum arcing chamber
2 材料属性和边界条件的设置
完成模型的建立后,需要对各个部分设置相应的材料特性。其中:导电杆、触头座、母排和套接的材料均为纯铜;触头支撑的材料为不锈钢;触头片的材料为CuCr50;屏蔽罩的材料为不锈钢。模型所用的材料属性如表1所示(真空的相对介电常数为1)。

表1 模型材料属性Tab.1 Properties of model material
边界条件的设置:对静触头及其金属连接件施加高电位(12 kV),动触头及其金属连接件为零电位;主屏蔽罩设置为悬浮导体;计算场域为模型的5倍,无限远边界处设置为零电位。
3 电场仿真计算结果
将电场仿真计算模型导入ANSYS有限元分析软件,然后按照材料属性和边界条件进行计算,得到中压真空灭弧室内部的电场分布,电场仿真模型纵向剖面的电场分布云图如图2所示。

图2 中压真空灭弧室内部电场分布云图Fig.2 Electric field distribution inside medium voltage vacuum arcing chamber
从图2可以看出,电场分布最密集的区域为触头间隙和触头片表面边缘处。为了更直接地显示电场分布,分别选取静触头表面沿直径方向的路径、动触头表面沿直径方向的路径和触头中心平面沿直径方向的路径,将这三条路径上的电场分布进行对比,触头表面与触头中心平面径向的电场分布曲线如图3所示。其中:静、动触头表面沿直径方向路径的取值位置为从触头表面的中心处沿触头表面径向方向到触头表面的外缘;触头中间平面沿直径方向路径的取值位置为从仿真模型的中心处沿触头中心平面径向方向到模型外缘。

图3 触头表面与触头中心平面径向的电场分布曲线图Fig.3 Radial electric field distribution curve of contact terminal surface and contact terminal center plane
从图3可以看出:1)动、静触头之间中心平面的电场强度虽然比较大(最大值为1.5×106V/m),但是这部分区域的电场分布比较均匀,不易发生放电。2)真空灭弧室内部电场强度的最大值出现在静触头表面边缘处,也就是触头间隙的边缘位置,最大值为1.62×106V/m,超过了动、静触头之间的中心平面的电场强度最大值。3)动、静触头表面的电场分布不均匀,在距离触头表面中心35 mm处,电场强度出现了快速的增大。4)静触头表面的电场强度大于动触头表面的电场强度。这是因为:以灭弧室样品的实际模型为基础建立的电场仿真模型的静端组件与动端组件不完全对称,静导电杆的长度小于动导电杆,而且静导电杆完全封闭在屏蔽罩内部,从而静端组件(静端触头和静导电杆)周围的电场全部集中在屏蔽罩内部。
4 真空灭弧室内部电场分布影响因素的分析
真空灭弧室绝缘性能的好坏主要取决于灭弧室内部的电场分布。研究真空灭弧室内部电场分布的影响因素,需要采用不同的电场模型进行对比仿真计算。在真空灭弧室长期的设计和应用实践中,表面光滑的电极在高真空度(P≤6.6×10-2Pa)间隙的电场耐受强度为107V/m。考虑到电场的不均匀系数、电极表面的状态和绝缘裕度等因素,在实际的真空灭弧室设计中,真空灭弧室内部的最大电场强度不应该高于 8 ×106V/m[5-6]。然而,真空灭弧室的绝缘性能不仅单纯与电场强度有关,更取决于灭弧室内部电场强度的最大值与最小值之差,即电场分布的均匀性,场强差越小,说明电场的分布越均匀,真空灭弧室的绝缘性能也越好。因此,采用对比计算的方式,阐述真空灭弧室中动静触头的开距、触头和悬浮屏蔽罩的形状等因素对灭弧室内部电场分布的影响。
4.1 触头开距对电场分布的影响
在之前的设计中,动、静触头之间的开距为8 mm。现改变触头开距,使其分别为8 mm、10 mm和11 mm,对从仿真模型中心处沿触头中心平面径向方向到模型外缘的区域和从静触头表面中心处沿触头表面径向方向到触头表面外缘路径的电场强度分别进行对比,得到不同触头开距下触头中心平面径向电场分布曲线和不同触头开距下静触头表面径向电场分布曲线如图4和图5所示。

图4 不同的触头开距下触头中心平面径向电场分布曲线Fig.4 Radial electric field distribution curve of contact terminal center plane under different contact terminal distance

图5 不同的触头开距下静触头表面径向电场分布曲线Fig.5 Radial electric field distribution curve of static contact terminal surface under different contact terminal distance
从图4和图5可以看出:随着动、静触头之间开距的增大,触头中心平面的电场强度减小,静触头表面的电场强度和灭弧室内部电场强度的最大值也随之减小,但是电场强度的分布趋势没有明显改变。这说明:改变触头之间的开距,只是可以降低灭弧室内部的电场强度,但是不能改变灭弧室内部的电场分布,不能降低场强差。所以,单纯改变动、静触头之间的开距,不能明显改善真空灭弧室的绝缘性能。
4.2 不同电极对电场分布的影响
虽然真空灭弧室动、静触头之间的电位差最大,场强较强,但是由于这部分区域的面积较大,因此电场分布比较均匀,耐压性能较好,动、静触头之间不易发生击穿。然而静触头表面的电场分布不均匀,在距离触头表面中心35 mm处(即触头边缘倒角处)电场强度出现了快速的增大,是真空灭弧室内部电场分布的最强点。分别对触头边缘为直角、倒圆角(半径1 mm和半径1.5 mm)情况下的电场模型进行计算,对从静触头表面中心处沿触头表面径向方向到触头表面外缘路径的电场强度进行对比,得到不同电极的静触头表面径向电场分布曲线如图6所示。

图6 不同电极的静触头表面径向电场分布曲线Fig.6 Radial electric field distribution curves of static contact surface at different electrode
从图6可以看出:1)触头外形中的棱边做圆倒角处理后,静触头表面的电场强度明显下降,电场分布更加均匀。2)触头外形中的棱边做圆倒角处理后,真空灭弧室内部的电场强度也明显减小,改善了真空灭弧室的绝缘性能。3)在一定范围内,随着触头边缘棱边圆倒角半径的增大,静触头表面的电场强度呈下降趋势。但需要的注意的是:在实际的设计中,要综合考虑各种因素来选择触头边缘圆倒角的半径,不能一味增大圆倒角的半径。这是因为:圆倒角半径的增大会减小触头之间实际的接触面积,引起触头表面电流密度的增大,导致真空电弧难以开断,从而影响真空灭弧室的开断性能。
4.3 屏蔽罩对电场分布的影响
触头与屏蔽罩之间的区域和屏蔽罩边缘区域的电场分布比较不均匀,影响了灭弧室的绝缘性能。因此,有必要分析屏蔽罩尺寸、翻边开口处的半径与朝向对灭弧室内部电场分布的影响,以使上述区域的电场分布更加均匀。
4.3.1 屏蔽罩半径对内部电场分布的影响
为研究屏蔽罩尺寸对真空灭弧室内部电场分布的影响,当其他条件不变时,只改变屏蔽罩的半径,对比计算真空灭弧室内部的电场分布。分别取屏蔽罩半径为46.25、48.75和51.25 mm时的情况进行分析,对从静触头下端面外缘处沿径向到屏蔽罩内侧路径的电场强度进行对比,得到不同屏蔽罩半径的真空灭弧室沿路径方向的电场分布曲线如图7所示。
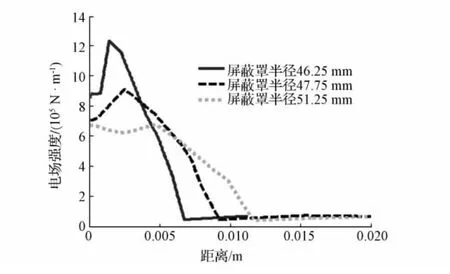
图7 不同屏蔽罩半径的真空灭弧室沿路径方向的电场分布曲线Fig.7 Electric field distribution curve of different shielding radius vacuum arcing chamber along the direction
从图7可以看出:1)从三条曲线的趋势来看,在静触头下端面的外缘处附近,电场强度快速上升,但是随着与静触头距离的增大,电场强度逐渐下降,并且最终趋于平缓。这是因为在静触头下端面的外缘处附近区域的面积较小,导致这部分区域的电荷分布相对集中,所以这部分区域的电场强度会快速上升。但随着与静触头距离的增大,电荷分布逐渐均匀,电场强度逐步下降,最终趋于平缓。2)屏蔽罩半径为46.25 mm时,所选路径最大电场强度为1.23×106V/m;而屏蔽罩半径增加到51.25 mm时,最大电场强度下降为6.75×105V/m。所以,在一定范围内,随着屏蔽罩半径的增大,屏蔽罩与触头之间的电场强度明显减小而且电场分布更加均匀。
4.3.2 屏蔽罩翻边开口处半径对内部电场分布的影响
为了研究屏蔽罩翻边开口处半径对周围电场分布的影响,当其他条件不变时,只改变屏蔽罩翻边开口处的半径,对比计算真空灭弧室内部的电场分布。取屏蔽罩翻边开口处半径分别为2.5、3和3.5 mm时的情况进行分析,对从屏蔽罩翻边处开口处内侧沿径向到屏蔽罩外缘的路径的电场强度进行对比,得到不同屏蔽罩翻边开口处半径的真空灭弧室沿路径方向的电场分布曲线如图8所示。

图8 不同屏蔽罩翻边开口处半径的真空灭弧室沿路径方向的电场分布曲线Fig.8 Electric field distribution curve in different shielding flange opening radius vacuum arcing chamber along the path
从图8可以看出:1)从三条曲线的趋势来看,在屏蔽罩翻边开口处附近电场强度快速上升,并且达到最大值,但随着与屏蔽罩翻边开口处距离的增大,电场强度逐步下降,最终趋于平缓。这是因为屏蔽罩翻边开口处的面积很小,这部分区域的电场分布也相对集中。虽然这部分区域的电场强度远低于动、静触头之间的电场强度,但是由于屏蔽罩翻边开口处的材料比较薄,绝缘性能比较差,所以此处也是真空灭弧室绝缘性能的薄弱点。2)屏蔽罩翻边开口处半径为2.5 mm时,所选路径最大电场强度为1.64×105V/m;而屏蔽罩翻边开口处的半径增加到3.5 mm时,最大电场强度下降为1.4×105V/m。所以,在一定范围内,随着屏蔽罩翻边开口处的半径的增大,屏蔽罩翻边开口处附近区域的电场强度略有减小而且电场分布更加均匀。
4.3.3 主屏蔽罩翻边开口朝向对内部电场分布的影响
为了研究屏蔽罩翻边开口朝向对周围电场分布的影响,在其余部分结构和条件不变的情况下,只改变屏蔽罩翻边开口的朝向,对比计算真空灭弧室内部的电场分布。分别取屏蔽罩翻边内翻与外翻时的情况进行分析,对屏蔽罩与静导电杆之间中线位置的路径的电场强度进行对比,得到不同屏蔽罩翻边朝向情况下沿路径方向的电场分布曲线如图9所示。
从图9可以看出:当保证同样绝缘间隙时,屏蔽罩翻边开口朝向灭弧室外侧时,所选路径的最大电场强度为3.37×105V/m;而屏蔽罩翻边开口朝向灭弧室内侧时,最大电场强度上升为3.52×105V/m。因此,屏蔽罩翻边开口朝向灭弧室外侧时,屏蔽罩与静导电杆之间区域的电场强度比较小。

图9 不同屏蔽罩翻边朝向情况下沿路径方向的电场分布曲线Fig.9 Electric field distribution curve of different shielding flanging towards the case along the path
5 结论
1)真空灭弧室内部电场强度的最大值出现在静触头表面边缘处,此处是绝缘的薄弱点。
2)单纯改变动、静触头之间的开距,真空灭弧室的绝缘性能不能得到明显改善。
3)在一定范围内,随着屏蔽罩半径的增大,屏蔽罩与触头之间的电场强度明显减小。
4)屏蔽罩翻边开口外翻时的屏蔽罩周围区域的电场分布比内翻时小,而且随着蔽罩翻边开口处半径的增大,翻边开口处附近区域的电场强度下降。
[1]NIMS J W.SMITH R E.Application of a genetic algorithm to power transformer design[J].Electric Machines and Power Systems,1995,24(10):669 680.
[2]SHOKICHI It O,KAWASE Y,MORI H.3D finite element analysis of magnetic blowout force acting on the arc in molded case circuit breakers[J]. IEEE Transaction on Magnetics,1997,33(2):2053 2056.
[3]WEXLER A.Finite-element field analysis of an inhomogeneous,an isotropic,reluctance machine rotor[J].Journal of Beijing Institute of Technology,1999,8(2):12 15.
[4]WEIMERS L.HVDC Light——A New Technology for a Better Environment[J].IEEE Power Engineering Review,1998,18(8):19 20.
[5]梁淑华,范志康,胡锐.CuCr50触头材料优化热处理工艺研究[J].金属热处理学报,2000(3):66 70.LIANG Shuhua,FAN Zhikang,HU Rui.Investigation on the optimum heat treatment process of CuCr50 contact materials[J].Transactions of Metal Heat Treatment,2000(3):66 70.
[6]李禹成.小型化真空灭弧室的研究与设计[D].西安:西安交通大学,2008.LI Yucheng.Study and design of small scale vacuum interrupter[D].Xi’an:Xi’an Jiaotong University,2008.
