复杂工况下的电磁性能测量技术

孔庆奕，程志光，李悦宁

(1．河北工业大学 电气工程学院，天津 300401;2．保定天威集团公司，河北 保定 071056;3．华北电力大学 电气与电子工程学院，河北 保定 071056)

大型电力变压器中的铁心和磁屏蔽采用高导磁性能的取向硅钢片叠积而成，对叠片铁心和磁屏蔽中的杂散损耗、局部过热问题的分析及其结构优化是电力变压器设计中的重点问题［1－2］。大量的研究结果表明，磁性材料中的电磁场分布和损耗分布结果的准确度和有效性归根结底取决于材料在实际工作状态下的电磁性能［3－4］，而电工材料供应商提供的电磁性能数据，例如取向硅钢片的铁损和磁化性能曲线，通常是在标准规定的条件下测量得出的。

爱泼斯坦方圈作为一种标准的用于测量硅钢片低频和一维磁性能的专用磁测量仪器已被广泛应用，其测量数据具有较好的重复性。与环形样件相比，爱泼斯坦方圈采用被测样片双搭接结构，具有制作相对简单、不须重复绕制励磁绕组和测量绕组等优点。然而爱泼斯坦方圈做为一种单相变压器铁芯模型，磁场、磁通密度、损耗和激磁功率仅仅在方圈每个铁轭中段认为是均匀分布的，角部搭接处的磁通密度和比总损耗的不均匀性增加并使得实际的磁路长度存在变数［5－8］。国际和国内所采用的电工钢片(带)测量方法规定标准爱泼斯坦方圈为25cm方圈，有效磁路长度被规定为0.94 m［9］。但是，标准爱泼斯坦方圈实际的等效磁路长度并不总是等于0.94 m，在非标准规定的测试条件下受很多因素影响。因此，这一量值在大多数情况下是不确切的，做如此假定将导致实质性的误差。

本文通过双爱泼斯坦方圈加权处理法，确定被测样片铁轭处的比总损耗和与磁性能相关的25cm方圈的有效磁路长度。通过测量样片剪切方向与轧制方向成不同角度的硅钢试样，并采用不同的激磁频率，分析不同情况下被测样片磁性能的变化规律，使仿真建模所使用的磁化曲线和损耗曲线更接近硅钢片真实的运行状态，从而增加仿真计算的有效性。

1 双爱泼斯坦方圈加权法原理

1.1 双方圈法确定有效磁路长度实验原理

爱泼斯坦方圈在转角处采用双搭接结构使该区域的磁密与“轭”中段的磁密不同，会给比总损耗测量带来影响，因此制作长度不等的25 cm和17.5 cm两种方圈。实验过程中需要保证两个方圈的转角处搭接结构中的磁通分布相同，小方圈的铁轭略小于大方圈的铁轭。分别在大小两个方圈上用同样的试件进行磁性能测量，之后用“做差”的方法将方圈损耗不均匀区域排除，得到与方圈损耗均匀区域相关的有效磁路长度，双方圈测量法原理如图1所示。

假设两个方圈总损耗的差值只与铁轭长度差有关，即图1中所示的搭接区域和相邻区域损耗分布情况相同，产生损耗差值的铁轭区域为E－25中段区域(假设这一区域的磁通密度分布和损耗分布是均匀的)，每条样片的有效测量区域长度差用ΔL表示，则两个方圈的损耗差可以表示为

式中:Pno为25 cm方圈的总损耗，W;Psm为17.5 cm方圈的总损耗，W;Pnc为25 cm方圈转角处的损耗，W;Pnl为 25 cm方圈铁轭处的损耗，W;Psc为17.5 cm方圈转角处的损耗，W;Psl为17.5 cm方圈铁轭处的损耗，W。

根据假设条件，Pnc=Psc，则式(1)可以改写为

与式(2)损耗差值对应的试样有效质量Δm为

式中mt为被测试样的总质量，则E－25的均匀区单位质量损耗Ploss可以表示为

与被测样片均匀区相关的有效磁路长度为

1.2 双方圈法测量激磁功率实验原理

用双方圈法表示激磁功率的公式为

式中:s为单位质量样件的激磁功率，VA/kg;ΔS为两方圈所测得的激磁功率差，m;Δm为两种不同规格方圈有效质量差，kg。

1.3 加权平均法确定铁心有效磁路长度原理

由于方圈均匀区和非均匀区的比总损耗不同，为了得到准确的等效磁路长度，需要考虑均匀区和非均匀区对等效磁路长度的影响。为了确定具有搭接结构的铁心的有效磁路长度，提出一种加权平均法，将基于铁心不同区域的比总损耗所确定的有效磁路长度做加权处理，具体方法如下:

令铁心加权处理的有效磁路长度为

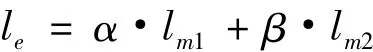
式中:lm1由E－25中段均匀区单位质量损耗Ploss1确定，lm2由E－25拐角处也即E－17.5的单位质量损耗Ploss2确定，α和β为权因子。参照式(3)有

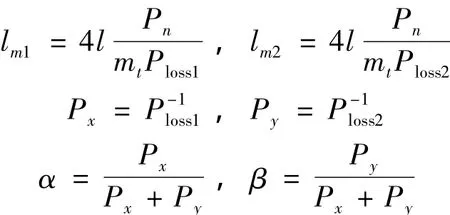
则式(4)可改写为

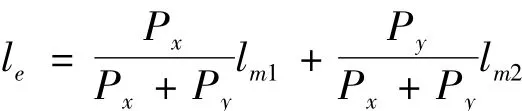
按照双方圈加权平均法测量出等效磁路长度le后，被测试样的比总损耗Ps按下式计算:

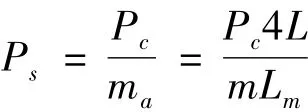
2 三维建模验证双方圈法的可行性

为了验证双爱泼斯坦方圈法的前提条件，即两个方圈的角部搭接区域磁通分布相同，进行三维建模，考察该区域磁密分布的一致性，观察其磁密云图和磁密分布情况，计算磁密大小得到准确的曲线走势。采用加拿大Infolytica公司的Magnet V7.2电磁仿真软件在三维时谐场进行计算，仿真模型如图2所示。

图2 25 cm爱泼斯坦方圈二分之一模型Fig.2 Half model of 25 cm Epstein frame

硅钢片选用型号为30q120，采用双搭接结构，用爱泼斯坦方圈测得频率为50 Hz，沿轧制方向(即与剪切方向成0°)的30q120硅钢片磁化曲线如图3所示。

图3 30p120硅钢片B－H曲线Fig.3 B－H curves of 30P120

硅钢片尺寸为300 mm×30 mm×0.3 mm，25 cm方圈四边激励绕组总匝数为700匝，每边为175匝，建二分之一模型(见图2)，激励电压为8.14 V。20 cm方圈激励绕组总匝数为520匝，每边为130匝，激励电压为5.98 V。17.5 cm方圈激励绕组总匝数为432匝，每边为108匝，激励电压为4.92 V。硅钢片每片总厚度3×10－4m，考虑到两边存在保护漆膜并且搭接时有一定气隙，若设叠片系数为 0.97，片间绝缘的厚度只有 0.3×3%=0.009 mm，故实际建模时每片厚度2.91×10－4m，两侧各留 4.5 ×10－6m 的气隙［11］。绕组选用TEAM21铜材料，电导率设为5.7143×107 S/m。

选取角部搭接区的中部，图2仿真模型中沿z轴正方向第三片内分别截取三个方圈角部搭接区的中线线段，得到该线段上的磁密曲线，如图4所示。

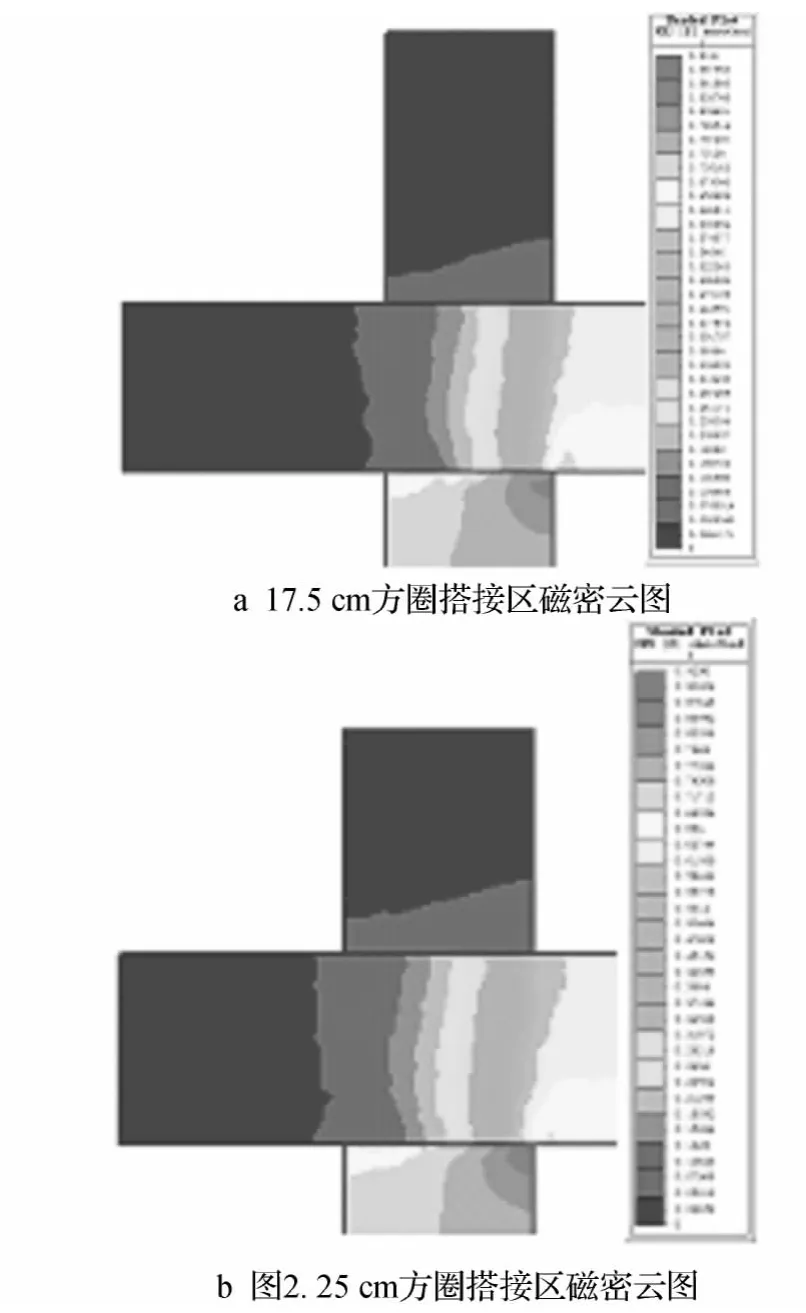
图4 双方圈搭接区磁密云图Fig.4 Magnetic clouds map of ring overlap block section

由图4可以看出，三者的大小与走势基本吻合，各磁密分布情况与大小也基本相同。由此，三维仿真结果验证了双爱泼斯坦方圈法的前提条件，即三个方圈的角部搭接区域磁通分布相同，是合理并具有意义。

3 实验计算结果与分析

3.1 实验装置和测试材料

实验所使用的硅钢样片30P120，每种样片尺寸均为30 mm×300 mm。双爱泼斯坦方圈实验使用WT3000功率分析仪测量Epstein方圈激磁功率的实验接线如图5所示。为保证测试电源稳定性，实验过程中使用UPS电源。

3.2 实验数据处理及结果分析

用E－25和E－17.5分别测量30P120系列样片(剪切方向与轧制方向成 0°，55°，90°)在频率50、100、150、200，300 Hz 情况下的磁化特性、损耗特性以及方圈的等效磁路长度。

3.2.1 等效磁路长度非标准工况下曲线

图5 使用WT3000测量Epstein方圈激磁功率Fig.5 Exciting power measured by power analyzer(WT－3 000)via Epstein frame

爱泼斯坦方圈加权法测量得到的30P120与轧制方向成0°、55°和90°硅钢片在不同工作频率(50，100，150，200 Hz)下的等效磁路长度变化曲线如图6所示。

图6 不同工作频率下的等效磁路长度变化曲线Fig.6 Equivalent magnetic circuit length curve under different working frequency

3.2.2 硅钢片比总损耗多工况下曲线

爱泼斯坦方圈加权法测量得到的30P120与轧制方向成0°、55°、90°硅钢片在不同工作频率(50，100，150，200 Hz)下的比损耗曲线，如图7所示。

从图7可以看出，随着剪切方向与轧制方向所成角度的变大，比总损耗变大，但是取样方向为55°和90°样片的比总损耗值比0(取样方向的大40%以上，但是取样方向为55°和90°样片的比总损耗值基本趋于一致，证明了55°试样的导磁性能低于其他角度试样的导磁性能。

图7 在不同工作频率下的比损耗曲线Fig.7 Ratio loss curve under different working frequency

3.2.3 多工况下硅钢片激磁伏安特性曲线

爱泼斯坦方圈测量得到的2E(25－17.5)、E25两种方法计算得到的不同频率下试样中段的激磁伏安曲线如图8—图11所示。

图8—图11中的结果显示，采取标准爱泼斯坦方圈法和双方圈法测得试样中端的激磁伏安数值基本趋于一致。

双方圈测量得30P120沿0°轧制方向下在不同频率下的激磁伏安变化曲线如图12所示。由图12可以得出，随着频率的增大，激磁伏安数值也在逐渐增大。

图8 激磁伏安(55°，50 Hz)Fig.8 Exciting power(55°，50 Hz)

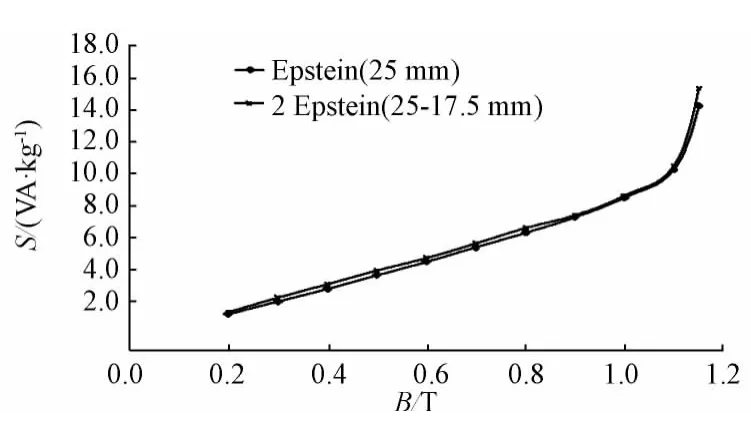
图9 中段激磁伏安(55°，100 Hz)Fig.9 Exciting power of sample in middle section(55°，100 Hz)

图10 激磁伏安(55°，200 Hz)Fig.10 Exciting power(55°，200 Hz)

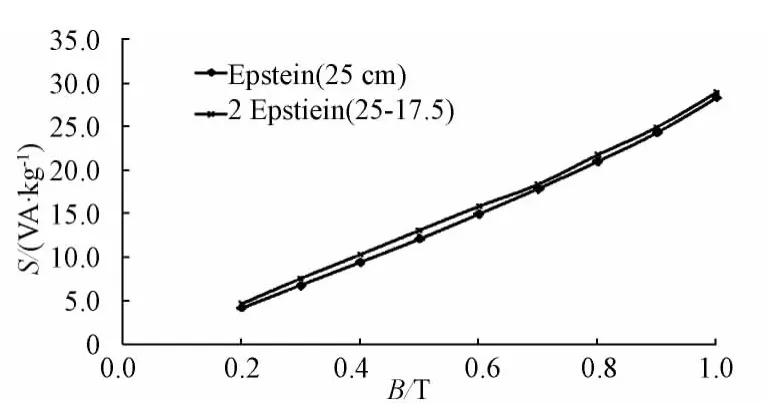
图11 激磁伏安(55°，300 Hz)Fig.11 Exciting power(55°，300 Hz)

4 结论

1)实验表明，25 cm方圈是由均匀区、搭接区构成，其等效磁路长度也受这两个因素的影响，不是一个固定不变的值，也会受取样轧制角度、频率、温度的影响。

图12 不同频率下的激磁伏安特性(0°，30P120)Fig.12 Exciting power under different frequence(0°，30P120)

2)由三维仿真结果得出了硅钢片在 E25，E20和E17.5三个方圈搭接区的磁密分布基本相同，磁密大小曲线基本一致，证明了双方圈法的前提条件基本符合实际。

3)基于双爱泼斯坦方圈加权处理方法测量不同工况下的磁性技术及获得的实验结果和结论性意见，对实际变压器铁心结构设计和铁心综合损耗系数评价具有参考价值。

［1］ CHENG Z，HAO R，TAKAHASHI N，et al．Engineering-oriented benchmarking of Problem 21 family and experimental verification［J］．IEEE Trans．on Magn．，2004，40(2):1394 1397．

［2］ CHENG Z，TAKAHASHI N，YANG S，et al．Loss spectrum and electromagnetic behavior of problem 21 family［J］．IEEE Trans．on Magn．，2006，42(4):1467 1470．

［3］ CHENG Z，TAKAHASHI N，YANG S，et al．Eddy current and loss analysis of multi-steel configuration and validation［J］．IEEE Trans．on Magn．，2007，43(4):1737 1740．

［4］ CHEN Z，TAKAHASHI N，FORGHANI B，et al．Analysis and measurements of iron loss and flux inside silicon steel laminations［J］．IEEE Trans．on Magn．，2009，45(3):1222 1225．

［5］谢德馨，杨仕友．工程电磁场数值分析与综合［M］．北京:机械工业出版社，2009．XIE Dexin，YANG Shiyou．Numerical analysis and summary of engineering electromagnetic field［M］．Beijing:China Machine Press，2009．

［6］程志光，高橋則雄，博札德·弗甘尼，等．电气工程电磁热场模拟和应用［M］．北京:科学出版社，2009．CHENG Zhiguang，Takahashi N，Forghani B，et al．Electromagnetic and thermal field modeling and application in electrical engineering［M］．Beijing:Mechanical Industry Press，2009．

［7］ MARKETOS P，ZUREK S，MOSES A J．Calculation of the mean path length of the Epstein frame under non-sinusoidal excitations using the double Epstein method［J］．Journal of Magnetism and Magnetic Materials，2008，320(20):2542 2545．

［8］ CHENG Z，HU Q，JIAO C，et al．Laminated Core Models for Determining Exciting Power and Saturation Characteristics［C］//World Automation Congress Proceedings．2008:1215 1218．

［9］GB/T 3655－2000．用爱泼斯坦方圈测量电工钢片(带)磁性能的方法［S］．北京:中国标准出版社，2001．