基于EEMD峰度阈值变压器振动信号降噪方法

刘福荣，孙福军，田 伟，姜述杰

(1．国网黑龙江省电力有限公司，哈尔滨 150090;2．环境保护部核与辐射安全中心，北京 100082)

变压器安全可靠运行是整个电网安全运行的关键，因此对其运行状态的实时检测十分必要。目前，基于振动信号分析的变压器故障诊断方法作为一种新型的诊断方法，具有实时性及在线运行的特点，现已在电力系统中广泛采用。然而工程中实际采集的信号都含有大量噪声，使得能反应故障特征的有效信息变得非常微弱，因此如何有效提取有用信号、抑制噪声、提高信噪比是基于振动信号进行故障诊断的前提条件和必要环节［1］。

针对非平稳信号的降噪，国内外学者已提出许多方法，大致可分为基于时间域统计、基于傅立叶变换及基于小波变换的时频分析方法三大类［1］。这些方法都有各自的优缺点，如:频域方法理论成熟，但难以分离频率重叠部分的信号;小波变换方法虽具有多分辨性能，但其降噪效果往往依赖于小波基和阈值的选择。经验模式分解(EMD)是Huang等人1997年提出的将多分量信号分解成多个固有模式分量(IMF)的方法［2］，这些IMF分量中的瞬时频率具有实际的物理意义，且频率由高到底依次分布，具有很强的频率选层性能，是一种完全自适应的分解方法。2008年Huang等人又提出了集合经验模式分解方法(EEMD)，将白噪声添加到含有奇异点的信号中以促进抗混分解，有效抑制了模式混叠现象［3］。目前学者们也尝试利用EEMD方法对信号进行降噪处理。文献［4］提出的利用白噪声经EEMD分解的各分量能量密度与平均周期是常数这一特点，对满足条件的噪声分量能进行剔除，但剔除的分量含有有用信号。文献［5］利用白噪声与普通信号自相关函数的差异性，先对含噪信号进行EMD分解，然后人为判断哪个IMF是噪声分量，再对噪声分量进行软阈值处理，该方法虽能有效抑制噪声，但噪声分量和有用分量的区分只能靠人为判断，具有一定主观性［6－10］。为此，本文提出一种利用峰度系数来度量白噪声与普通信号自相关函数差异性的方法。首先对信号进行EEMD分解，然后针对每一个IMF进行自相关函数计算并求其峰度系数，利用阈值将这些IMF进行区分，进而剔除噪声信号。实验中将本文方法应用到仿真信号和变压器实际振动信号进行降噪处理并同其他方法进行比较，结果表明本文方法的性能优于其他降噪方法。

1 理论分析

1.1 EMD原理及其模式混叠

EMD可以同时将一个信号不同尺度(频率)的波动或趋势逐级分解开，产生一系列具有不同特征尺度的数据序列，称为本征模函数(Intrinsic Mode Function，IMF)。为了使每一个IMF分量求解的瞬时频率具有物理意义，要求每个IMF分量具有如下特征:1)从全局特性上看，极值点数和过零点数一致或至多相差一个;2)在某一个局部点，极大值包络和极小值包络在该点的值的算术平均和是零。

在EMD分解步骤中求解均值是整个算法的关键。常用的方法是利用两个三次样条函数分别对信号的所有极大值点和极小值点进行拟合得到信号的上、下包络线，并计算出包络的均值曲线，将原信号减去该均值曲线后，重新求取极值点上、下包络线及包络均值，依次往复，直至不满足给定门限条件。在此分解步骤中，若信号存在奇异点(如间断点或脉冲等)［8－9］，极值点的分布就会发生改变，从而影响上、下包络线及其均值的求取，进而影响每个IMF分量的求取，表现为某些IMF不再具备固有模式的两个条件，发生模式混叠现象。

1.2 EEMD原理及其分解步骤

为了克服EMD模式混叠缺点，EEMD方法将白噪声多次加入到原始信号中，以此来平滑奇异点的影响。其原理是利用白噪声频谱均匀分布的特性，使得加入白噪声后的信号经EMD分解后自动平均分解到不同时间尺度上。由于白噪声具有零均值特性，将多次分解后的IMF平均后可完全消除噪声影响，即可得到最终无混叠效应的IMF分量。具体算法如下:

1)在原始信号x(t)中加入M次均值为零、标准方差为常数的白噪声ni(t)(i=1，…，M)。

2)对加入白噪声的信号xi(t)进行EMD分解，得到K个IMF分量和一个残余分量ri(t)。

3)利用白噪声统计特征均值为零的特点，将每次分解的IMF分量和残余分量分别进行平均运算，消除每次加入白噪声的影响，进而也抵消了奇异点引起的混叠现象。

式中:ck(t)为最终信号分解的第k个IMF分量;r(t)为最终信号分解的残余分量。

4)利用上述得到的IMF分量和残余分量进行原始信号的重构，即

1.3 基于自相关函数峰度阈值的降噪方法

随机信号的自相关函数反应了信号与其自身在不同时间点的相关程度，是一种时间域的统计度量方法，其定义为

式中Rx(0)表示信号与自身在同一时刻的相关函数值，显然，对于任何随机信号而言这一值都最大。自相关函数是信号间隔的函数，间隔有正负间隔，所以n个长度的信号，有2n－1个自相关函数值，分别描述的是不同信号间隔的相似程度，也体现了自相关函数的对称性。

考虑到白噪声自相关函数的特点，即只与自身相关，其他情况几乎为零，这与一般信号的自相关函数不同，其结果如图1所示。

为了能定量描述相关函数的特点，引入峰度值作为相关函数分布特征的指标。峰度系数(Kurtosis)用来度量数据在中心聚集程度。在正态分布情况下，峰度系数值是0。正的峰度系数说明观察量更集中，有比正态分布更长的尾部;负的峰度系数说明观测量不集中，有比正态分布更短的尾部。

图1 随机噪声和一般信号的自相关函数形状对比Fig.1 Autocorrelation function shape comparison of random noise and normal signal

式中:N代表样本个数;σ为样本集合的标准方差。

峰度是用来反映分布曲线顶端尖峭或扁平程度的指标，值越大则越陡峭。图1中的一般信号自相关函数的峰度值为4.0622，而随机信号自相关函数的峰度值为114.0381。可见，随机信号的自相关函数分布极其陡峭。

基于EEMD自相关函数峰度阈值的降噪方法流程描述为:首先对信号进行EEMD分解，然后计算每一个IMF的自相关函数并求得其峰度值，依据峰度值判断是否满足随机噪声的自相关函数特征，将大于阈值的IMF分量剔除，保留非噪声IMF分量并将其重构得到去噪后的信号。因为该方法不要求噪声只出现在高频部分，所以可以保留有用的高频信号分量，其中阈值的设定为10。该流程如图2所示。

2 实验分析及讨论

2.1 仿真评测数据

仿真信号采用频率为10 Hz的余弦信号，其中t=0～1 s，采样频率为 1000 Hz。加均值为0、标准差为0.1的随机噪声后，进行EEMD分解(令白噪声次数M=5，标准差0.05)，原始信号和加噪信号如图3所示，前4个IMF及其频谱图如图4所示，前4个自相关函数图如图5所示。其中它们的峰度值分别为 314.8461，104.2123，80.3738，2.7018。根据阈值可知，前3个都是噪声，只有第4个IMF为有用信号。从图4中的频谱可以看出只有IMF4在10 Hz左右。

图2 基于EEMD自相关峰度阈值去噪方法流程图Fig.2 Flow chart of de-noising method based on EEMD autocorrelation kurtosis threshold

图3 原始信号和噪声信号Fig.3 Original signal and noised signal

为了进一步验证本文降噪方法的有效性，仿真过程中加入标准差不同的随机噪声，观察并计算结果，并将加入方差为0．3的噪声信号的降噪结果与小波db8软阈值降噪和EMD降噪方法进行比较，如表1所示。其中降噪性能指标:输出信噪比和输入输出波形相似度，降噪效果如图6和图7所示。

表1 本文降噪方法与小波软阈值及EMD降噪对比结果Tab.1 Comparison of the three de-noising methods

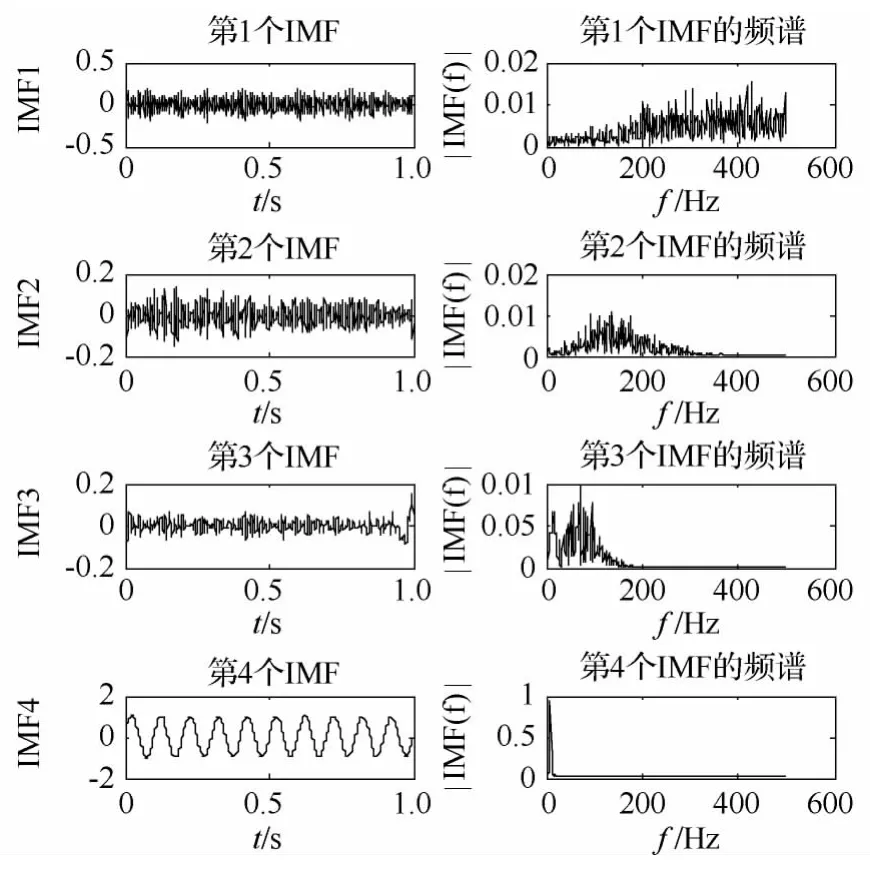
图4 前4个IMF分量及其频谱图Fig.4 Previous 4 IMFs and their spectrums

图5 前4个IMF分量的自相关函数图Fig.5 Autocorrelation function of the previous 4 IMFs

表1 中数据表明，本文降噪方法相对于小波db8软阈值降噪和EMD降噪方法具有较明显的优势。

输出信噪比计算表达式为

输入输出波形计算表达式为

图6 不同方差噪声去噪后的信噪比Fig.6 SNR of denoised signal with different noise standard varies

图7 不同方差噪声去噪后的波形相似度比Fig.7 Wave similarity of de-noised signal with different noise standard varies

式中:xo为输出信号值;x为原始未加噪声信号值。

2.2 实例实验

实验数据利用振动加速度传感器从变压器箱体上采集箱体振动信号。信号采样频率为10 kHz，采样点数1000个，并将振动数据送至PC机上进行处理。振动信号及重构信号如图8所示，EEMD分解加入0.05标准方差噪声，集成个数为50。前4个IMF及其频谱如图9所示，可以看出第一个IMF呈现噪声特性，其自相关函数的峰度值为80.6。

本文方法同小波方法和EMD方法进行比较的实验结果如表2所示。

图9 前4个IMF分量及其频谱图Fig.9 Previous IMFs and their spectrums

表2 本文降噪方法与小波软阈值及EMD降噪对比结果Tab.2 Comparison of the three de-noising methods

从表2结果可以看出，本文方法的降噪效果同样优于其他两种方法。

3 结语

本文提出一种基于EEMD的降噪方法，应用EEMD方法实现含噪信号的分解，然后利用随机噪声与一般函数的自相关函数分布特征不相同的特点，再用峰度值定量描述每一个IMF分量的自相关函数分布特征，进而通过阈值判断剔除噪声信号，拾取有用信号。仿真实验和实例实验表明:采用该方法得到的信噪比和波形相似度都优于其他两种去噪方法。

［1］丁康，陈健林，苏向荣．平稳和非平稳振动信号的若干处理方法及发展［J］．振动工程学报，2003，16(1):1 6．DING Kang，CHEN Jianlin，SU Xiangrong．Some processing methods for stationary and non-stationary vibration signal and its development［J］． Journal of Vibration Engineering，2003，16(1):1 6．

［2］ HUANG N E，SHEN Z，LONG S R，et al．The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis［J］．Proc．R．soc．London A ，1998，454:903 995．

［3］ WU Z H，HUANG N E ．Ensemble empirical mode decomposition:a noise assisted data analysis method［J］．Advance in Adaptive Data Analysis，2009，1(1):1 41．

［4］陈仁祥，汤宝平，马婧华．基于EEMD的振动信号自适应降噪方法［J］．振动与冲击，2012，31(15):82 86．CHEN Renxiang，TANG Baoping，Ma Jinghua．Adaptive de-noising method based on EEMD for vibration signal［J］．Journal of Vibration and Shock，2012，31(15):82 86．

［5］王婷．EMD算法研究及其在信号去噪中的应用［D］．哈尔滨:哈尔滨工程大学，2010．Wang Ting．Research on EMD algorithm and its Application in signal denoising［D］．Harbin:Harbin Engineering University，2010．

［6］ YEH J R，SHIEH J S．Complementary ensemble empirical mode decomposition:A noise enhanced data analysis method［J］．Advances in Adaptive Data Analysis，2010，2(2):135 155．

［7］ TERRIEN J，MARQUE C，KARLSSON B．Automatic detection of mode mixing in empirical mode decomposition using nonstationarity detection:application to selecting IMFs of interest and denoisong［J］．EURASsIP Journal on Adavances in Signal Processing，2011，2011:37．

［8］宋立新，王祁，王玉静，等．具有间断事件检测和分离的经验模态分解方法［J］．哈尔滨工程大学学报，2007，28(2):178183 SONG Lixin，WANG Qi，WANG Yujing，et al．Empirical mode decomposition method with discontinuous event detection and separation［J］．Journal of Harbin Engineering University，2007，28(2):178 183．

［9］邵忍平，曹精明，李永龙．基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断［J］．振动与冲击，2012，31(8):96 101．SHAO Renping，CAO Jingming，LI Yonglong．Gear fault pattern identification and diagnosis using Time-Frequency Analysis and wavelet threshold de-noising based on EMD［J］．Journal of Vibration and Shock，2012，31(8):96 101．

［10］蔡剑华，王先春，胡惟．基于经验模态分解与小波阈值的MT信号去噪方法［J］．石油地球物理勘探，2013，48(2):303 307．CAI Jianhua，WANG Xianchun，HU Wei．A de-noising method for MT signal based on EMD and wavelet threshold ［J］．OGP，2013，48(2):303 307．