考虑转向操纵机构万向节间隙的车辆摆振系统动力学行为分析*

卢剑伟，辛加运，张士路，Theodossiades Stephanos

(1.合肥工业大学机械与汽车工程学院，合肥 230009;2.拉夫堡大学Wolfson机械与制造工程学院，拉夫堡 LE113TU)

前言

摆振是车辆较为常见的一种质量缺陷，严重的摆振会影响车辆的操纵稳定性和行车安全，并导致其动力性、燃油经济性和乘坐舒适性降低，因此近些年来受到越来越多的关注［1-4］。

导致车辆发生摆振的因素很多，如轮胎侧偏特性，悬架与转向系统结构参数匹配不当和转向系间隙等。在以往针对车辆摆振的研究中，国内外学者从动力学分析角度对其开展了一系列讨论，取得了很多重要的成果。如文献［5］中在轮胎侧向力与回正力矩的数学建模方面进行了长期研究，形成了稳态侧偏特性的基本理论;文献［6］中进一步研究了适合于载荷与侧偏角大范围内变化的轮胎侧偏特性，并进一步对非稳态侧偏特性进行了深入研究;文献［7］中通过试验分析了前轮定位参数和轮胎与车辆使用条件等因素对摆振的影响;文献［8］中建立了包括全部前轮定位参数的前轮摆振数学模型，并对车轮绕主销和车桥绕纵轴两自由度之间的陀螺耦合和弹性耦合在摆振中起的作用做了确切的阐述。然而，由于新车的摆振问题更易引起人们的关注，而间隙引发的摆振只在旧车中较为常见，因此上述研究中大多没有考虑间隙的影响。但是，文献［5］中以转向传动机构中存在间隙为例，通过对车辆摆振系统动力学的分析发现，转向系间隙对于摆振响应有很大影响［4］。

在车辆转向系操纵机构中，由于转向盘个性化调整的需要，转向柱与转向器输入轴之间存在一定夹角，并且夹角可能会因转向盘角度的调整而变化，因此在转向操纵机构中须采用万向节传动。由于制造装配误差，万向节间隙不可避免，由此可能会对转向系摆振产生影响。本文中以十字轴式万向节为例，考察十字轴轴颈与万向节叉之间的间隙对车辆摆振系统动力学响应的影响，相关结论有助于更好地实现车辆摆振控制，并为万向节工艺参数的优化提供理论依据。

1 含间隙十字轴式万向节动力学建模

图1为十字轴式万向节示意图，φ1为主动轴转角，φ2为从动轴转角，α为主从动轴之间的夹角。由于制造装配需要，在万向节十字轴轴颈与轴承内复圆之间存在径向间隙，如图2所示。为简化分析模型，假定主动轴两套孔与十字轴轴颈存在径向间隙，而从动轴与十字轴轴颈不存在间隙。

十字轴在运动时自身机构的约束关系［9］为

式中:φs为十字轴与主动轴连接端轴颈的转角;φr为十字轴与从动轴连接端轴颈的转角。

十字轴与从动轴无转角误差，即φ2=φr，而十字轴与从动轴之间转角误差可记为

十字轴端的间隙大小为

式中Rs为十字轴端到十字轴中心的长度。主动轴叉与十字轴端通过圆柱滚子接触，其相互作用力可用等效无质量弹簧-阻尼系统描述，记为

其中弹性力为

式中k为等效刚度，且有

式中r为十字轴端间隙。

万向节间隙接触等效阻尼力为

式中c为等效阻尼系数，且有

2 计入转向操纵机构万向节间隙的车辆摆振系统动力学建模

基于如下假设，建立图3所示的计入万向节间隙的车辆摆振系统动力学模型。

(1)车辆保持匀速直线行驶，且转向盘固定。

(2)传动杆件视为刚性杆，不考虑其它传动间隙。

(3)忽略转向器中摩擦等损失及操纵机构杆轴弹性变形。

图中，θ1、θ2分别为右转向轮和左转向轮的摆角;L为前桥轮距;R为车轮半径;ψ为前桥侧摆角。

万向节主动轴的动力学平衡方程为

其中 φ1=θ2iw2

式中:M为作用于左转向轮的转向力矩;Id为主动轴转动惯量;M1为主动轴作用于十字轴的转矩;iw1为左转向节臂到转向器输入端的等效力矩传动比;iw2为左转向节到转向器输入端的等效角传动比。此外，转向盘固定，因此φ2=0。十字轴动力学平衡方程为

式中Is为十字轴转动惯量。

将式(10)代入式(9)，可得

右转向轮绕主销动力学平衡方程为

式中:I1为转向轮绕主销转动惯量;I2为转向轮绕自身轴线转动惯量;c1为换算到主销的横拉杆阻尼;c4为车轮绕主销的当量阻尼;k1为换算到主销的横拉杆刚度;k4为轮胎侧向刚度;k5为轮胎垂向刚度;v为车速;l为主销延长线与地面交点到车轮对称面距离;γ为主销后倾角;f为轮胎与地面摩擦因数;T1为右轮胎动态侧偏力;β为轮胎拖距。

左转向轮绕主销动力学平衡方程为

式中:c2为换算到主销的直拉杆阻尼;T2为左轮胎动态侧偏力。

前桥侧摆的动力学平衡方程为

式中:I3为前桥绕其纵轴线转动惯量;c3为换算到前桥侧摆中心的悬架当量角阻尼;k3为换算到前桥侧摆中心的悬架当量角刚度。

将式(12)～式(14)写成如下状态方程形式:

3 数值分析［10］

基于上述模型，对车辆摆振系统进行动力学分析，系统结构参数如表1所示。

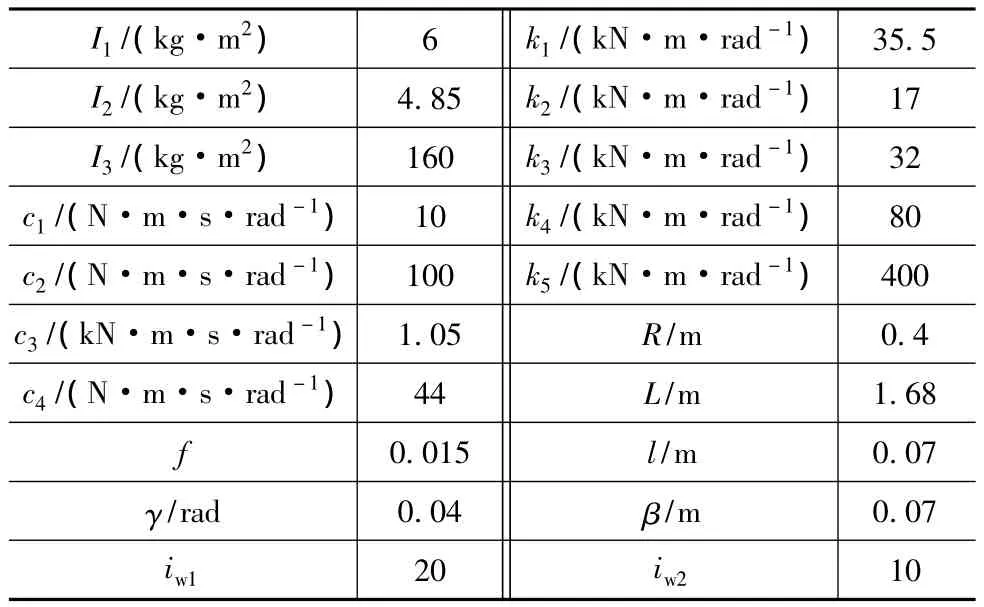
表1 系统结构参数

图4和图5分别为同一车型在无间隙和有间隙时的转向轮摆角随车速变化情况。可以看出，两种情况下剧烈摆振的车速区间始终为45～72km/h，没发生变化;但有间隙时，转向轮摆角明显增大;同时，考虑间隙时转向轮摆角运动形态趋于复杂，在剧烈摆振车速区间外，转向轮的响应出现了分岔现象。

图6和图7分别为车速30和56km/h时考虑间隙的转向轮摆振响应。可以看出，车速为30km/h时，转向轮出现了拟周期分岔;而在车速为56km/h时，转向轮运动收敛于稳定的极限环。其它车速下的分析结果也符合图5所示的规律，不予赘述。

4 结论

(1)转向操纵机构万向节间隙对车辆摆振系统动力学响应的影响较大，在车辆摆振系统动力学分析中应计入操纵机构间隙的影响。

(2)与不考虑转向操纵机构万向节间隙的摆振系统相比，间隙对摆振系统响应的影响主要体现为运动形态的变化，通常不会改变发生剧烈摆振的车速区间。此外，考虑间隙的转向轮摆角明显增大。

(3)对于考虑万向节间隙的摆振系统，在发生剧烈摆振车速区间外，转向轮出现了拟周期分岔现象，而在摆振车速区间内，转向轮运动收敛于稳定的极限环。

［1］ Gordon J T.Perturbation Analysis of Nonlinear Wheel Shimmy［J］.Journal of Aircraft，2002，39(2):305-317.

［2］ Lin Y，Li S.Study on the Bifurcation Character of Steering Wheel Self-excited Shimmy of Motor Vehicle with Dependent Suspension［J］.Chinese Journal of Mechanical Engineering，2004，40(12):187-191.

［3］ Virgile A，Vinod C，Nader J.Experimental Testing and Validation of Tangential Steering Wheel Vibrations due to Tire Nonuniformity［J］.ASME Dynamic Systems and Control Division，2005，74(1):545-551.

［4］ Lu Jianwei，Gu Jue，Liu Mengjun.Modeling of the Vehicle Shimmy System with Consideration of Clearance of the Steering Mechanism［J］.Meccanica，2010，45(1):53-61.

［5］ 酒井秀男.タイヤ工学［M］.东京:づうこづり株式会社，1987.

［6］ 郭孔辉.汽车操纵动力学［M］.长春:吉林科学技术出版社，1991.

［7］ 殷涌光，郁工瑞，程悦荪.拖拉机前轮摆振及稳定性判定［J］.农业机械学报，1984，16(1):1-14.

［8］ 宋健，管迪华.前轮定位参数与轮胎特性对前轮摆振影响的研究［J］.汽车工程，1990，12(1):13-25.

［9］ 朱金榴.万向联轴器十字轴的运动学和动力学方程［J］.上海工程技术大学学报，1996，10(3):26-30.

［10］ 陈予恕.非线性振动［M］.北京:高等教育出版社，2002.