润湿特性对多孔介质缓慢干燥过程影响的数值模拟

程 树，吴 睿，崔国民，李延铭

（上海理工大学 能源与动力工程学院新能源所，上海 200093）

润湿特性对多孔介质缓慢干燥过程影响的数值模拟

程 树，吴 睿，崔国民，李延铭

（上海理工大学 能源与动力工程学院新能源所，上海 200093）

采用二维孔隙网络模型，对不同孔隙结构下亲水多孔介质与憎水多孔介质的缓慢干燥过程进行模拟，考察润湿特性的改变对二维多孔介质干燥过程中液相分布、蒸发速率以及干燥总时间的影响。模拟结果表明，忽略重力与黏性力影响时，多孔介质干燥过程只受毛细压力控制，亲水多孔介质蒸发端为无规则形状，而憎水多孔介质蒸发端则根据孔隙尺寸分布与喉孔比的不同呈现不同的特性；干燥总时间与润湿特性、蒸发速率、孔隙结构相关；当喉孔比相同时，紧凑多孔介质的干燥总时间小于非紧凑多孔介质；当喉孔比较小时，亲水多孔介质的干燥总时间小于憎水多孔介质；当喉孔比较大时，憎水与亲水多孔介质的干燥总时间可以近乎相等。

多孔介质；干燥；孔隙网络模型；润湿特性；喉孔比

多孔介质干燥是工业生产中的一个重要环节，主要用于食品干燥、轻质油回收、质子交换膜燃料电池等方面［1-2］。在一些领域中，多孔介质表现为亲水特性，干燥过程类似于排水过程［3-4］。而在一些特殊领域如质子交换膜燃料电池气体扩散层等，多孔介质则表现为憎水特性，其干燥过程可类比为自吸过程。

孔隙网络模型作为一种有效方法可应用于研究多孔介质的干燥过程。自Daian等［5］和Nowicki等［6］率先提出孔隙网络模型以来，Prat等［7-8］结合入侵逾渗理论提出了多孔介质干燥孔隙网络模型。此后，重力［9-10］、黏性力［11-13］、热效应［14-16］、拓扑结构［17-21］等影响多孔介质干燥的外界因素在建模过程中被考虑。另一方面，针对干燥过程中出现的液膜效应［22-23］、收缩现象［24］进行的研究进一步完善了多孔介质干燥的孔隙网络模型。

近年来，Pillai等［19,25］对亲水多孔介质干燥过程进行了研究。但对憎水多孔介质的研究还较少。吴睿等［26］采用三维孔隙网络模型对质子交换膜燃料电池气体扩散层水分蒸发的干燥过程进行模拟。近期，Wu等［27］采用三维孔隙网络模型研究孔隙结构对憎水多孔介质蒸发过程的影响，指出孔隙结构是影响憎水多孔介质干燥特性的重要因素。Chapuis等［28］在研究相同孔隙结构多孔介质蒸发过程时发现，憎水多孔介质蒸发端相对平整，而亲水多孔介质蒸发端为不规则状态。Lenormand［29］指出在不同孔喉比的情况下，自吸过程的两相流动特性截然不同。由此可见，润湿性对多孔介质的影响与其孔隙结构密切相关。但润湿性的变化对不同孔隙结构多孔介质干燥的影响尚未明确。

本工作对不同孔隙结构多孔介质润湿特性的影响进行研究，考察相位分布、蒸发速率、蒸发总时间对多孔介质干燥特性的影响。

1 孔隙网络模型

孔隙网络模型是将多孔介质抽象为理想的几何形状，复杂的孔隙空间由喉道及其相连的孔隙构成，喉道代表较小的空间，孔隙代表喉道交接处较大的空间。采用二维方形孔隙网络模型，其中，孔隙为正方形，连接两个相邻孔隙的为矩形截面的喉道，二维孔隙的网络模型见图1。

孔隙半径为孔隙边长的一半，取值区间为[rpmin，rpmax]：

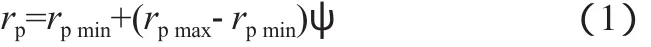
式中，ψ为0～1之间的随机数。

连接孔隙i和j的喉道半径（rt）为喉道横截面边长的一半，表示为

式中，λ为喉孔比，是孔隙网络模型的结构参数，通常情况下λ≤1。相邻孔隙之间的距离（l）为定值，设为25 μm。另外，孔隙网络模型中孔隙网络大小也是影响多孔介质蒸发过程的一个重要因素，为了更为详细地观察蒸发过程中孔隙网络中的两相流动特性，采用较小的孔隙网络（设定为20×20）。

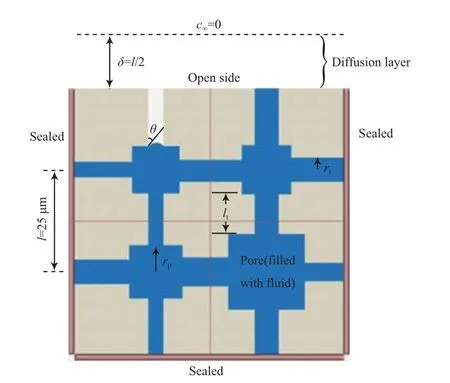
图1 二维孔隙的网络模型Fig.1 2D pore-network models.

由于只考虑缓慢蒸发过程，因此两相流动只受毛细力的控制，黏性力的影响则可忽略。在此情况下，多孔介质蒸发过程的两相流动可以视为准静态过程。蒸发过程中，每个孤立液体团中门阙流动阻力最小的单元（孔隙或喉道）将被驱替。单元的门阙流动阻力与单元尺寸和润湿性相关。以憎水多孔网络为例，喉道门阙流动阻力（Pct）［29］可由式（3）计算。

式中，σ为表面张力，取值0.072 N/m；θ为接触角，接触角的大小与介质的润湿性有关，憎水多孔介质θ取值60°，在润湿性不变的情况下θ不变。

孔隙门阙流动阻力（Pcp）［27］可由式（4）计算。

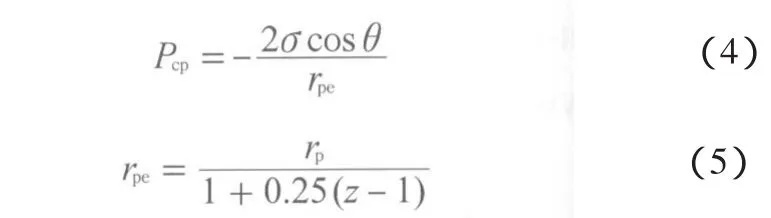
式中，rpe为有效孔隙半径；z为孔隙周围被气相占据的喉道数，z=1～3。亲水Pcp的计算式与式（3）相同。

由于孔隙周围被气相占据的喉道数目不同，根据式（4）计算的Pcp有3种不同的结果，故喉道和与之相邻孔隙之间的门阙流动阻力根据z的不同而改变。这与亲水多孔网络有着根本的不同。亲水多孔网络中，亲水多孔介质θ的取120°，计算孔隙阻力时均采用实际尺寸而非有效孔隙半径［30］，由于喉道尺寸小于相邻孔隙，故Pcp大于相邻孔隙。一旦喉道被侵入则相邻孔隙自动被侵入。

初始状态时孔隙网络完全充满液态水，水蒸气扩散只通过不封闭的上界面进行。在计算中做如下简化假设：1）忽略黏性力和重力的作用；2）水蒸气扩散过程为准静态过程；3）整个干燥过程在恒温条件下进行；4）水蒸气视为理想气体。

由以上假设条件，位于模型开口界面处的喉道与外界环境相接触，由菲克定律可得：

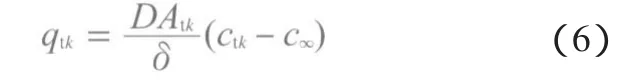
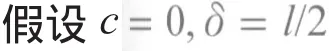
孔隙网络模型内部被气相占据的孔隙j的水蒸气蒸发量可由质量守恒原理得到：

式中，qpitij为孔隙i到喉道ij（连接孔隙i与孔隙j的喉道）的水蒸气蒸发量，可由菲克定律得到：

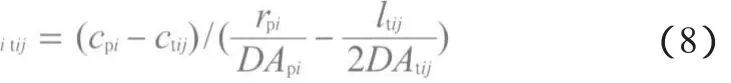
若孔隙或喉道两者中有一项为液相，那么该项的水蒸气浓度等于饱和水蒸气浓度，即cpi=1或ctij=1。

通过以上分析，多孔介质干燥过程的孔隙网络模型模拟算法可归纳为：1）确定网络模型中的液体团；2）根据质量守恒定理迭代计算孔隙网络中每个被气相占据的孔隙中水蒸气的扩散量；3）确定每个液体团中具有最小门阙流动阻力的单元；4）通过计算液体团中每个含有液相的单元和与其比邻的气相单元之间的扩散量来确定每个液体团的总蒸发量；5）确定每个液体团中具有最小门阙流动阻力单元中液体被完全蒸发所需时间，并确定最小时间；6）根据第5）步中确定的最小时间所在的单元更新计算网络模型的相分布；7）重复1）～6）步。

2 结果与讨论

主要分析润湿性对不同结构多孔介质干燥过程的影响。多孔介质的润湿性可由液相接触角表征。多孔介质结构用孔隙分布和喉孔比来表征。构建两种多孔网络：一为紧凑多孔网络，其孔隙半径分布区间较小，为5.5～6.5 μm；二为非紧凑多孔网络，其孔隙半径分布区间较大，为0～12 μm。此外，通过改变多孔网络的喉孔比（0.1，0.8，1.0），以获得润湿性对不同孔隙结构多孔介质干燥过程的影响。

2.1 液相分布

多孔介质干燥特性与其内部液相分布相关。为了揭示润湿性对多孔介质干燥过程的影响，对比不同液相饱和度情况下多孔介质干燥过程的液相分布。液相饱和度为含有液体的单元体积与孔隙网络中所有单元体积之比。

紧凑多孔介质的干燥过程见图2。由图2可知，喉孔比较小的憎水多孔介质，蒸发过程呈现几乎平整蒸发端，即蒸发过程逐行进行。多孔介质侵入过程只由毛细压力控制，因此比较Pct和Pcp能进一步解释蒸发侵入过程。憎水多孔介质侵入过程中，喉道和周围被气相占据喉道数目不同的孔隙的门阙流动阻力大小排序为：

式中，Pcp（1），Pcp（2），Pcp（3）为孔隙周围被气相占据喉道数目分别为1，2，3的Pcp。因此，对于喉孔比较小的憎水紧凑多孔介质，门阙流动阻力小的表面喉道优先被侵入，第一层喉道完全侵入后，位于第二层的孔隙才开始蒸发，而直到第二层孔隙蒸发完全后蒸发过程才在第三层喉道中进行，故蒸发端呈平整下降。而当喉孔比为1时，孔隙与喉道尺寸差距小且连接相邻两孔隙的喉道尺寸以较小喉道尺寸为基准，故喉道与孔隙之间的门阙流动阻力大小顺序为：Pct≥Pcp。此时，侵入竞争发生在整个多孔介质空间不同尺寸的喉道与孔隙之间，其干燥相图表现为毛细指径现象。而对于亲水多孔介质，蒸发相图均呈现为毛细指径现象，且喉孔比的变化对蒸发过程的影响不明显。

非紧凑多孔介质的干燥过程见图3。在非紧凑多孔介质空间内，尺寸相差较大的孔隙和喉道呈随机分布。根据入侵逾渗理论，憎水多孔介质蒸发过程选择侵入门阙流动阻力最小的孔隙或喉道，由于这个孔隙和喉道可能出现在孔隙网络模型中的任意一处，所以无论多孔介质的润湿性如何，干燥相图都呈现出毛细指径现象，而且相同饱和度下喉孔比的变化对蒸发过程的影响不大。

对比图2和图3中憎水多孔介质的蒸发相图可以发现：喉孔比较小的憎水紧凑多孔介质蒸发相图中只在最后一行边界处存在孤立的孔隙；喉孔比较大的紧凑多孔介质相图中既存在孤立喉道又存在孤立的孔隙。而非紧凑多孔介质中，喉孔比较小的多孔介质干燥过程中只出现孤立的孔隙，此孤立孔隙可以出现在孔隙网络中的任意位置；喉孔比较大的多孔介质干燥过程中既有孤立的孔隙又存在孤立的喉道。由此可见，孔隙结构不同的多孔介质干燥过程中相位分布存在着差异，且喉孔比对憎水多孔介质相位分布的影响更大。

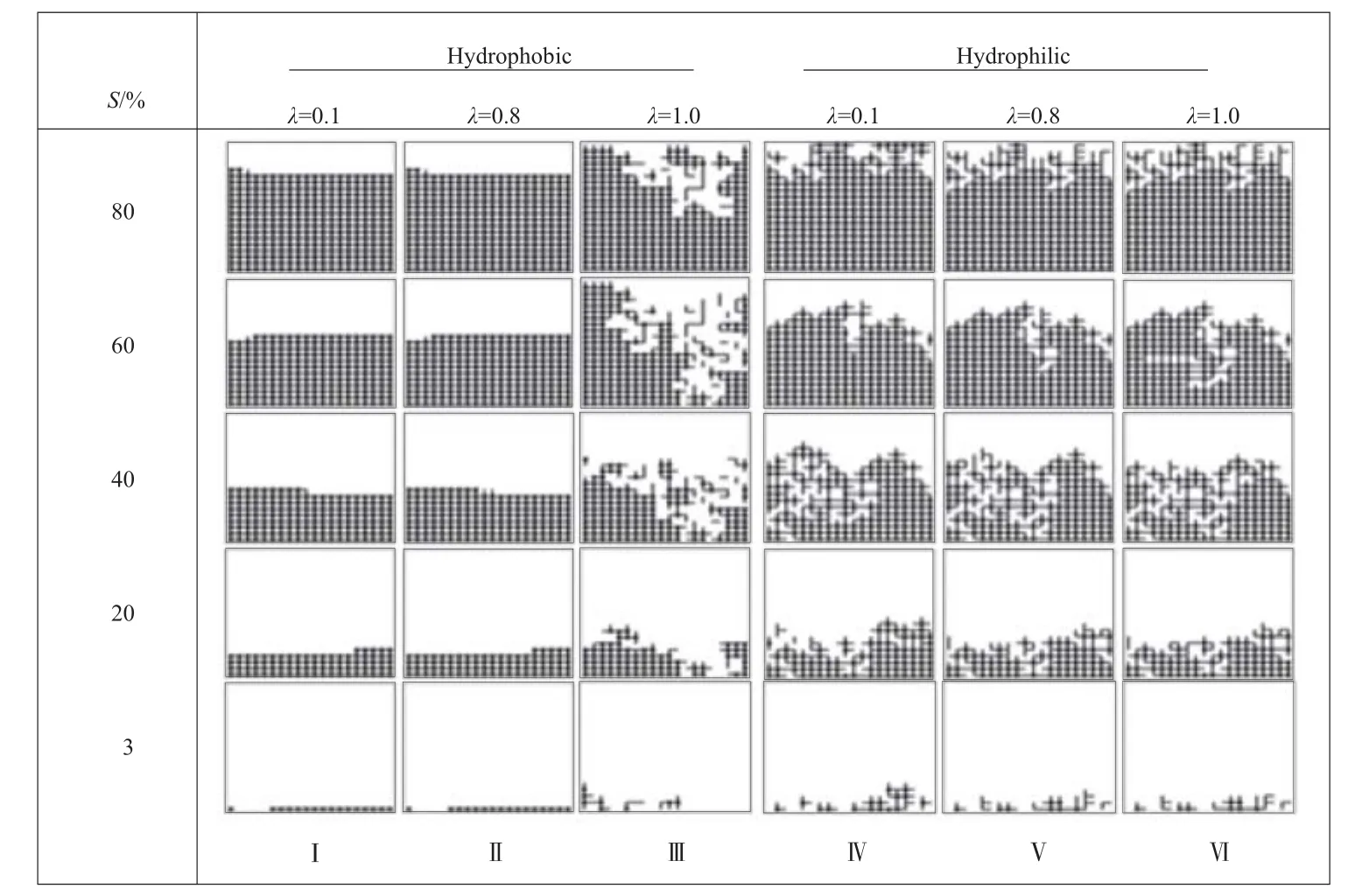
图2 紧凑多孔介质的干燥过程Fig.2 Drying process of porous media with narrow pore size distribution(PSD). Points represented the pores dominated by liquid， and lines denoted throats， the same below.

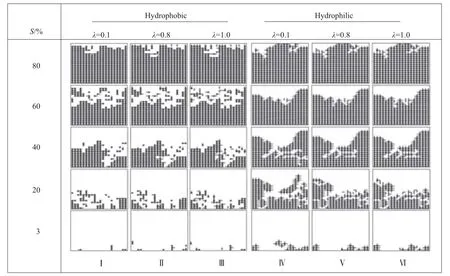
图3 非紧凑多孔介质的干燥过程Fig.3 Drying process of porous media with wide PSD.

为解释这一现象，取憎水孔隙网络的某孤立小液团部分进行具体分析。无孤立喉道气相侵入的原理见图4。对于喉孔比小于1的多孔介质，无论孔隙尺寸如何分布，与孔隙相连的喉道尺寸一定小于孔隙尺寸（见图4a）。由于憎水多孔介质的侵入过程发生在最小门阙流动阻力处，所以蒸发首先在喉道t1中进行，此后按门阙流动阻力等级依次在t2，t3，t4中进行。随着t4的蒸发完全，孔隙网络中出现了孤立的孔隙p1（p1为微元中最大的孔隙，见图4b）。憎水紧凑多孔介质当蒸发进行到最后一行时，位于边界处的Pcp（1）大于其他位置的Pcp（2），故在蒸发相图中为孤立孔隙，且只存在孤立孔隙。对于喉孔比等于1的多孔介质，孔隙尺寸分布不同的多孔介质存在着不同的现象。

图4 无孤立喉道气相侵入的原理Fig.4 Schematic diagram of gas introduction into un-isolated throats.

无孤立孔隙气相侵入的原理见图5。由于紧凑多孔介质的相邻孔隙的尺寸差距较小，假设p2和p3为微元中的最大孔隙，且rp2=rp3（见图5a）则rp2=rp3=rt23，两孔隙周围与空气接触的喉道t1～t6先于孔隙p2，p3，t23被侵入（见图5b）。之后，蒸发在孔隙p2和p3间随机选择，若p2被侵入则孔隙网络中留有孔隙p3和喉道t23（见图5c）。此时，孔隙p3周围被气相占据的喉道数为1，侵入过程随之随机发生在孔隙p3和喉道t23之间，若p3被侵入，则孔隙网络中出现孤立的喉道（见图5d），若t23被侵入，则出现孤立孔隙。另外，非紧凑多孔介质，由于其孔隙尺寸取值范围较大，上述两种情况皆可能出现。

当小液团中只有一个最大尺寸孔隙时，蒸发过程如图4所示，而小液团中具有两个相同尺寸的孔隙时，蒸发过程则如图5所示。

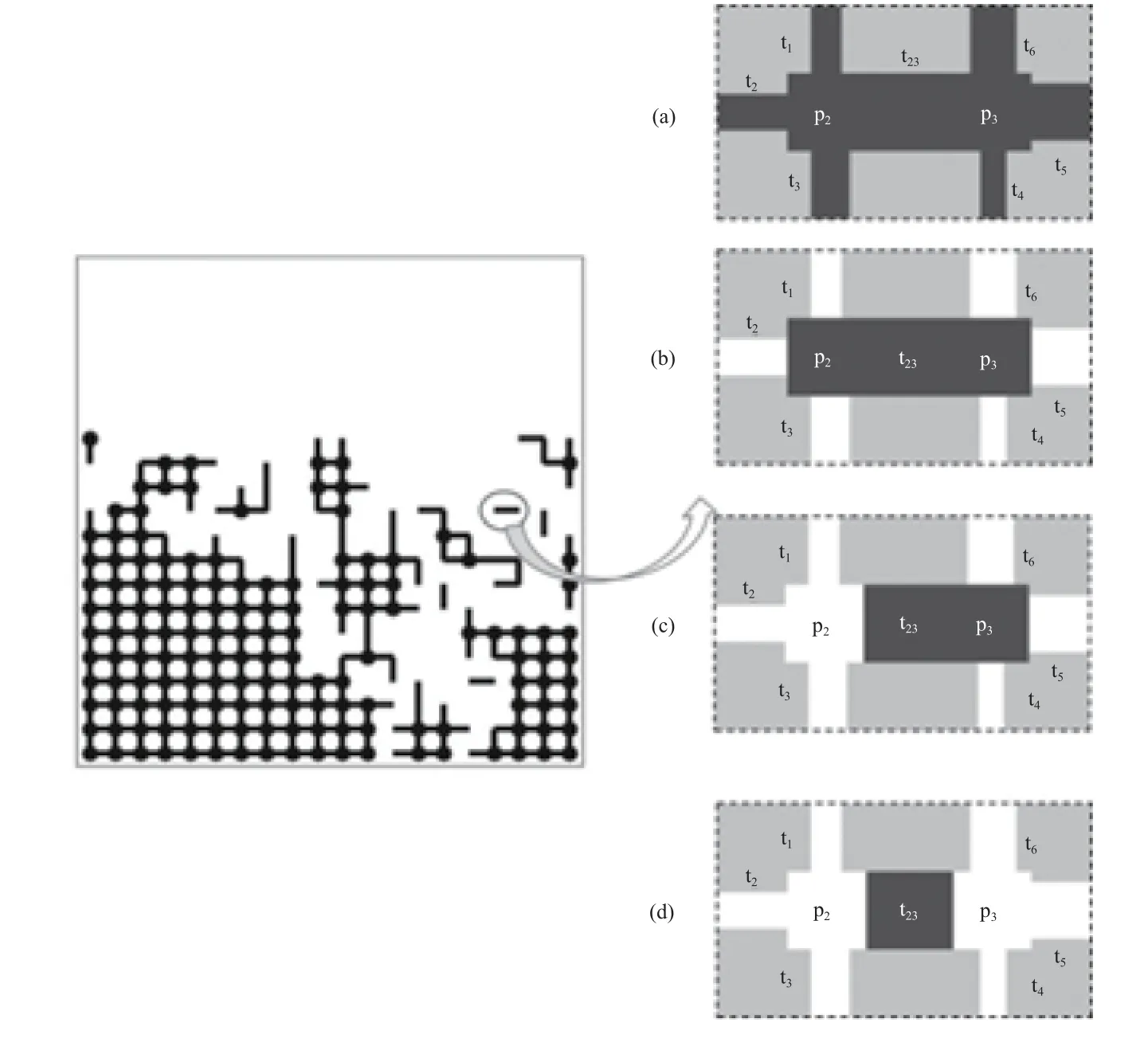
图5 无孤立孔隙气相侵入的原理Fig.5 Schematic diagram of gas introduction into un-isolated pores.

2.2 蒸发速率

润湿性与孔隙结构的变化使得多孔介质中液相分布趋势随之改变，而这一改变直接影响多孔介质液相饱和度的变化趋势。给出不同孔隙结构多孔介质的液体饱和度-时间曲线以揭示液体饱和度随蒸发时间的变化趋势。多孔介质干燥过程中液体饱和度随蒸发时间的变化关系见图6。

从图6可看出，无论多孔介质的孔隙尺寸分布是否紧凑，小喉孔比多孔介质的液相饱和度缓慢下降，而大喉孔比多孔介质的液相饱和度则极速下降。

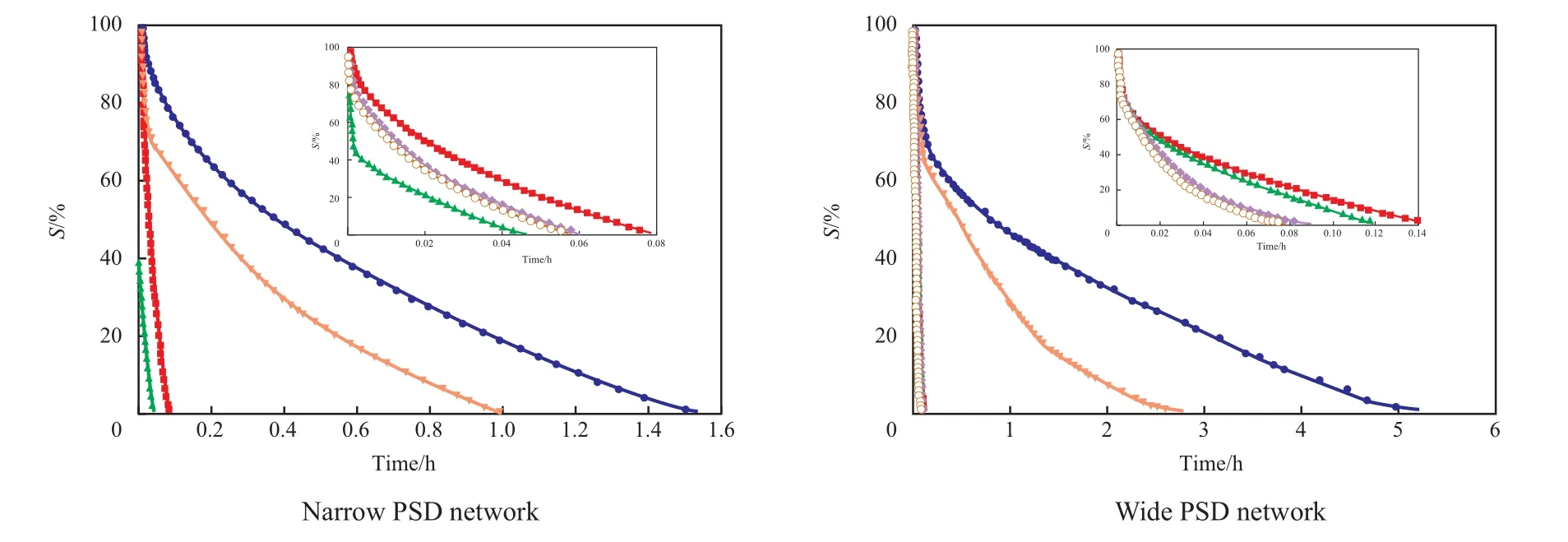
图6 多孔介质干燥过程中液相饱和度随蒸发时间的变化趋势Fig.6 Variation of S with evaporation time.

由液相饱和度与时间的关系可以得到蒸发速率的变化趋势。在不同喉孔比条件下不同多孔介质中的无量纲蒸发速率的结果见表1。从表1可看出，无量纲蒸发速率基本上随喉孔比的增加而减小。通过计算一个微元网络中瞬时蒸发速率来解释多孔介质蒸发速率的变化规律。微元网络的蒸发原理见图7。

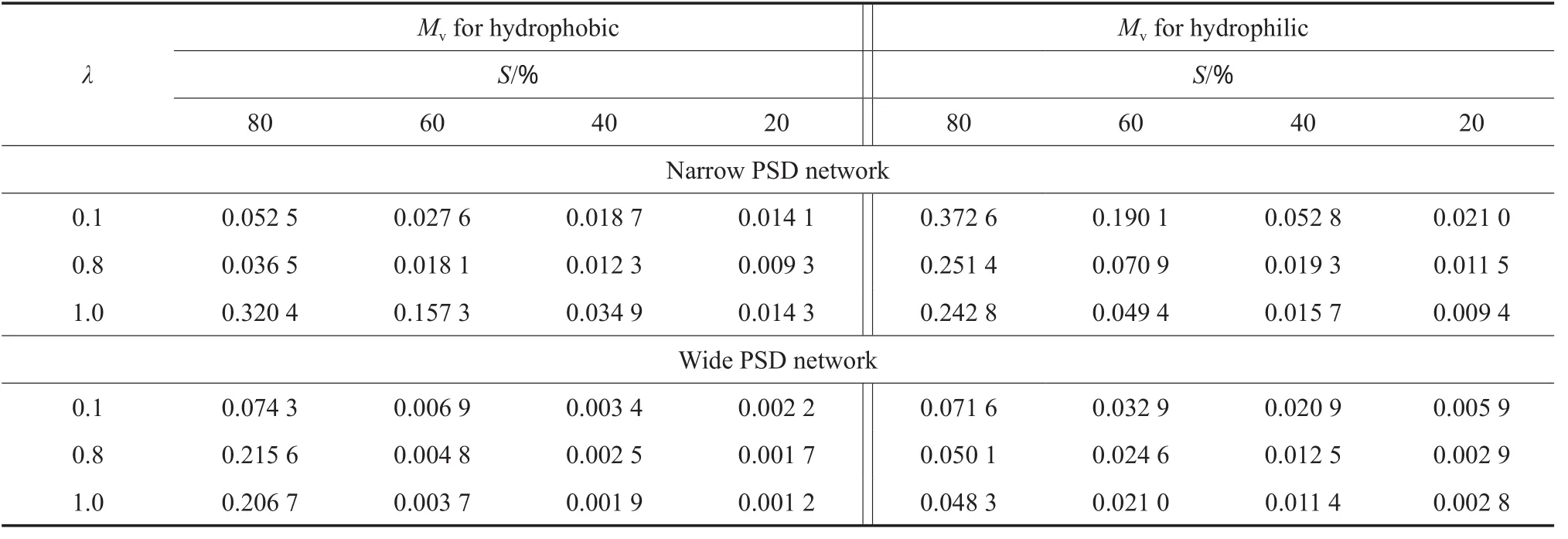
表1 在不同喉孔比条件下紧凑和非紧凑多孔介质中的无量纲蒸发速率Table 1 Non-dimensional evaporation rate(Mv) in the narrow and wide PSD networks at different λ

图7是一个1×1的二维孔隙网络，除上界面外其他3个界面皆封闭。假设初始状态孔隙与喉道完全充满液体，表面喉道中的液体与外界相连。随着蒸发的进行，蒸发端下降至孔隙中点位置。由菲克定律可知，初始状态微元网络的蒸发量（q）为：

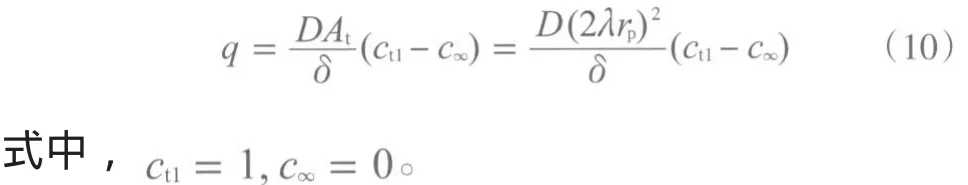
随着蒸发的进行，当孔隙中一半的液体已被蒸发，此时的孔隙中的蒸发量qpt1为：

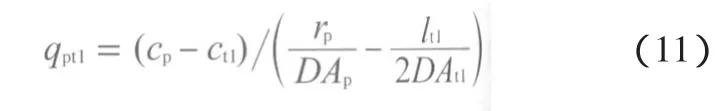
喉道与外界的蒸发量qt13为：

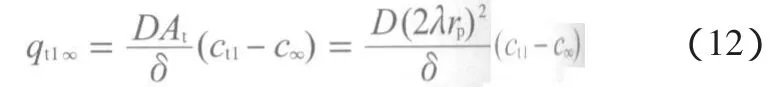
由式（14）可知，J随喉孔比的增大而减小。

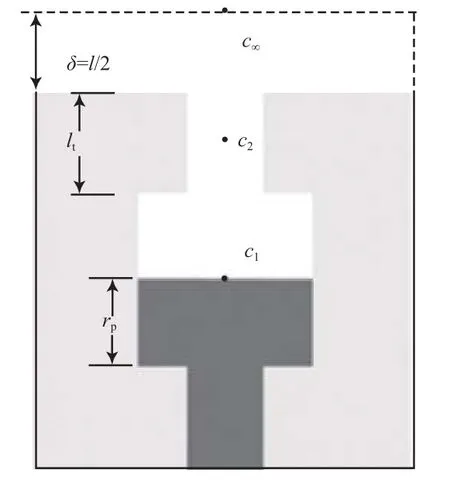
图7 微元网络的蒸发原理Fig.7 Schematic diagram of the evaporation for microelement network.

2.3 干燥总时间

喉孔比对干燥总时间的影响见图8。从图8可知，在相同的喉孔比条件下，紧凑多孔介质的干燥总时间小于非紧凑多孔介质。多孔介质干燥总时间本质上由多孔介质空隙体积与蒸发速率二者联合竞争决定。

多孔介质空隙体积为多孔介质内部孔隙与喉道体积之和。非紧凑多孔介质的空隙体积大于紧凑多孔介质，则在相同的喉孔比条件下，紧凑多孔介质的所需干燥总时间比非紧凑多孔介质更短。

由图8可见，随喉孔比的增大，紧凑多孔介质和非紧凑多孔介质的干燥总时间均呈现出先陡降再缓降最后趋于平衡的趋势；随喉孔比的增大，亲水与憎水多孔介质的干燥时间之间的差距逐渐缩小。其原因在于喉孔比较小时，亲水多孔介质在干燥初期开口上界面还留有部分与外界相连的喉道，这些表面喉道为干燥过程提供了较高的蒸发速率，从而缩短了蒸发时间，而憎水多孔介质在干燥初期与外界相连的表面喉道已被蒸发，所以其蒸发速率较小，从而干燥完全所需时间较长。当喉孔比较大时，亲水与憎水多孔介质干燥初期都存在部分表面喉道，整个干燥过程中的平均干燥速率相似，所以它们的干燥总时间接近。

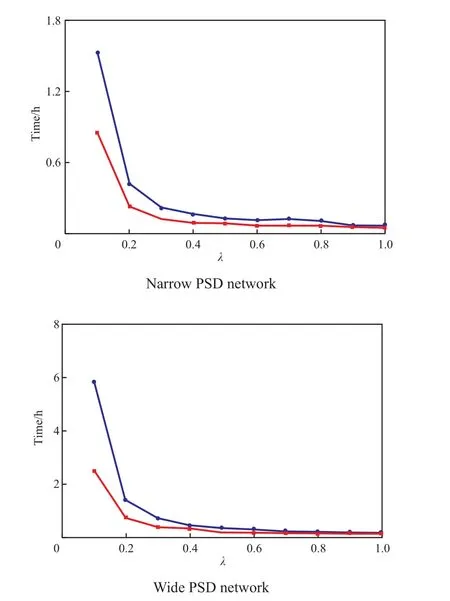
图8 喉孔比对干燥总时间的影响Fig.8 Effects of different λ on the total drying time.

由图8还可见，当喉孔比较小时，亲水多孔介质的干燥过程比憎水多孔介质快，这一现象与文献［29］给出的结论相同；当喉孔比较大时，亲水与憎水紧凑多孔介质干燥总时间几乎相等，其原因在于喉孔比为0.1～0.8时，憎水紧凑多孔介质蒸发逐行进行，表面喉道快速蒸发阶段持续时间短暂，此后蒸发速率降低，因而所需干燥时间较长，而亲水多孔介质在干燥初期由于表面喉道蒸发阶段持续时间较长，所以蒸发速率快。而在干燥后期，多孔介质被突破后，主液体团被撕裂成许多小液团，从而引起了较高的蒸发速率。因此，亲水多孔介质的蒸发速率总大于憎水多孔介质。当喉孔比为0.9～1.0时，憎水多孔介质的蒸发不再逐行进行，而是呈现与亲水多孔介质类似的毛细指径现象，且在达到突破前已经被撕裂成许多小液团。小液团蒸发速率较快，造成憎水多孔介质的蒸发速率非常接近于亲水多孔介质，从而使得两种不同润湿性多孔介质的干燥时间相近。

3 结论

1） 憎水紧凑多孔介质，喉孔比较小时蒸发端平整，喉孔比较大时蒸发端无规则形状；不同喉孔比的亲水紧凑多孔介质蒸发端形状不规则。非紧凑多孔介质，润湿性的改变对蒸发端的影响较小。

2）喉孔比较大的多孔介质干燥过程中既存在孤立的孔隙又存在孤立的喉道。当喉孔比较小时，憎水紧凑多孔介质蒸发相图中只在最后一行边界处存在孤立的孔隙，非紧凑多孔介质中孤立孔隙可出现在孔隙网络中的任意位置。

3） 随喉孔比的增大，亲水和憎水的多孔介质蒸发速率均减小。

4） 当喉孔比相同时，紧凑多孔介质的干燥总时间小于非紧凑多孔介质；当喉孔比较小时，亲水多孔介质的干燥总时间小于憎水多孔介质；当喉孔比较大时，憎水与亲水多孔介质的干燥总时间可以近乎相等。

［1］ 陈永利，曹立勇，何威，等. 分形多孔介质的孔隙特性对气体扩散的影响［J］. 化工学报，2011， 62（11）：3024 -3029.

［2］ 马亮，何榕. 分形多子L介质中气体的非稳态扩散［J］. 化工学报，2013， 64（9）：3139 - 3144.

［3］ Prat M. Recent Advances in Pore-Scale Models for Drying of Porous Media［J］.Chem Eng J，2002，86（1/2）：153 - 164.

［4］ Metzger T，Tsotsas E. Network Models for Capillary Porous Media［J］.Chem Ing Tech，2010，82（6）：869 - 879.

［5］ Daian J F，Saliba J. Determining a Representative Pore-Network for Moisture Sorption and Migration in Cement Mortar［J］.Int J Heat Mass Transfer，1991，34（8）：2081 - 2096.

［6］ Nowicki S C，Davis H T，Scriven L E. Microscopic Determination of Transport Parameters in Drying Porous Media［J］.Dry Technol，1992，10（4）：926 - 946.

［7］ Prat M. Percolation Model of Drying Under Isothermal Conditions Inporous Media［J］.Int J Multiphase Flow，1993，19（4）：691 - 704.

［8］ Tsimpanogiannis I N， Yortsos Y C， Poulou S， et al. Scaling Theory of Drying in Porous Media［J］.Phys Reν E：Stat，Nonlinear，Soft，Matter Phys，1999，59 （4）：4353 - 4365.

［9］ Laurindo J B，Prat M. Numerical and Experimental Network Study of Evaporation in Capillary Porous Media：Phase Distribution［J］.Chem Eng Sci，1996，51（23）：5171 - 5185.

［10］ Yiotis A G，Tsimpanogiannis I N，Stubos A K，et al. Pore Network Study of the Characteristic Speriods in the Drying of Porous Materials［J］.J Colloid Interface Sci，2006，297（2）：738 - 748.

［11］ Yiotis A G，Stubos A K，Boudouvis A G， et al. A 2-D Pore-Network Model of the Drying of Single Component Liquids in Porous Media［J］.Adν Water Res，2001，24（3/4）：439 -460.

［12］ Metzger T，Irawan A，Tsotsas E. Isothermal Drying of Pore Networks：Influence of Friction for Differentpore Structures［J］.Dry Technol，2007，25（1/3）：49 - 57.

［13］ Metzger T，Tsotsas E. Viscous Stabilization of Drying Front：Three-Dimensional Pore Network Simulations［J］.Chem EngRes Des，2008，86（7A）：739 - 744.

［14］ Plourde F，Prat M. Pore Network Simulations of Drying of Capillary Porous Media. Influence of Thermal Gradients［J］.Int J Heat Mass Transfer，2003，46（7）：1293 - 1307.

［15］ Surasani V K，Metzger T，Tsotsas E. Consideration of Heat Transfer in Pore Network Modeling of Convective Drying［J］.Int J Heat Mass Transfer，2008，51（9/10）：2506 - 2518.

［16］ Surasani V K，Metzger T，Tsotsas E. Influence of Heating Mode on Drying Behavior of Capillary Porous Media：Pore Scale Modeling［J］.Chem Eng Sci，2008，63（21）：5218 -5228.

［17］ Metzger T，Irawan A，Tsotsas E. Inf uence of Pore Structure on Drying Kinetics：A Pore Network Study［J］.AIChE J，2007，53（12）：3029 - 3041.

［18］ Surasani V K，Metzger T，Tsotsas E. Drying Simulations of Various 3D Pore Structure by a Nonisothermal Pore Network Model［J］.Dry Technol，2010，28（5）：615 - 623.

［19］ Pillai K M，Prat M，Marcoux M. A Study on Slow Evaporation of Liquids in a Dual-Porosity Porous Medium Using Square Network Model［J］.Int J Heat Mass Transfer，2009，52 （7/8）：1643 - 1656.

［20］ Segura L A，Toledo P G. Pore-Level Modeling of Isothermal Drying of Pore Networks：Effects of Gravity and Pore Shape and Size Distribution on Saturation and Transport Parameters［J］.Chem Eng J，2005，111（2/3）：237 - 252.

［21］ Yiotis A G，Tsimpanogiannis I N，Stubos A K. Three-Dimensional Modeling of the Evaporation of Volatile Hydrocarbons from Anisotropic Porous Media［J］.J Porous Media，2010， 13（3）：209 - 219.

［22］ Yiotis A G，Boudouvis A G，Stubos A K，et al. Effect of Liquid Films on the Drying of Porous Media［J］.AIChE J，2004，50（11）：2721 - 2737.

［23］ Yiotis A G，Stubos A K，Boudouvis A G，et al. Pore Network Modeling of Isothermal Drying in Porous Media［J］.Trans Porous Media，2005，58 （1/2）：63 - 86.

［24］ Thomas Metzger，Evangelos Tsotsas. Network Models for Capillary Porous Media：Application to Drying Technology［J］.Chem Ing Tech，2010，82 （6）：869 - 879.

［25］ Sghaier N，Prat M，Nasrallah S B. On the Infuence of Sodium Chloride Concentration on Equilibrium Contact Angle［J］.Chem Eng J，2006，122（1/2）：47 - 53.

［26］ 吴睿，朱恂，廖强，等. PEMFC气体扩散层干燥过程孔隙网络模拟［J］. 工程热物理学报，2011，32（1）：97 - 100.

［27］ Wu Rui，Cui Guomin，Chen Rong. Pore Network Study of Slow Evaporation in Hydrophobic Porous Media［J］.Int J Heat Mass Transfer，2014，68（1）：310 - 323.

［28］ Chapuis O，Prat M. Influence of Wettability Conditions on Slow Evaporation in Two-Dimensional Porousmedia［J］.Phys Reν E：Stat，Nonlinear，Soft，Matter Phys，2007，75（4）：046311.

［29］ Lenormand R. Liquids in Porous Media［J］.J Phys：Condens Matter，1990，2（1）：79 - 88.

［30］ Prat M. Discrete Models of Liquid-Vapour Phase Change Phenomena in Porous Media［J］.Reνue Générale Thermique，1998，37（11）：954 - 961.

（编辑 李治泉）

Numerical Simulation of Influence of Wetting Property on Slow Drying of Porous Media

Cheng Shu, Wu Rui, Cui Guomin, Li Yanming
（Institute of New Energy Science and Engineering，School Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China）

The slow drying processes of hydrophilic and hydrophobic porous media with different pore structure were simulated by using a pore network model and the inf uences of wetting property on evaporation behavior were investigated. The simulation results indicated that when adhesion and gravity were ignored，capillary pressure dominated the drying processes; the drying front ends in the hydrophilic porous media kept irregular shape，but in the hydrophobic porous media the drying front ends showed different features according to the pore size distribution(PSD) and throat-pore ratio; the total drying time was affected by the evaporation rate，pore structure and wetting property. For the wide PSD network，the total drying time of the hydrophilic porous media is less than that of the hydrophobic porous media when the throat-pore ratio is low. For the narrow PSD，the total drying time of the hydrophobic porous media is similar to that of the hydrophilic porous media when the throat-pore ratio is high.

porous media；evaporation；pore network；wetting property；throat-pore ratio

1000 - 8144（2014）09 - 1035 - 09

TQ 021.4

A

2014 - 03 - 27；［修改稿日期］ 2014 - 06 - 06。

程树（1988—），女，浙江省安吉市人，硕士生，电邮 shucheng1022@gmail.com。联系人：吴睿，电话 021 -55270155，电邮 ruiwu1986@gmail.com。

国家自然科学基金青年自然基金项目（51306124）；上海市自然科学基金青年项目（13ZR1458300）；重庆大学教育部重点实验室开放基金项目（LLEUTS-201305）；沪江基金研究基地专项（D14001）。