力磁耦合作用下电磁超声换能器换能效率仿真分析

宋小春，王亚午，李羽可

SONG Xiao-chun，WANG Ya-wu，LI Yu-ke

（湖北工业大学 机械工程学院，武汉 430068）

0 引言

作为油、水、气、浆液等流体运输工具之一的长输管道，常常工作在比较特殊或恶劣的环境中，经过一定时间的运行后，会出现锈蚀、腐蚀、裂纹等缺陷。为防止发生管道腐蚀穿孔、爆管等恶性事故，许多国家都制定了相应的法律、法规，以加强对在役管道的安全管理。但由于检测手段的制约，往往造成盲目开挖、盲目报废，维修缺少科学性，从而导致大量的资源浪费。而基于磁致伸缩效应的电磁超声检测技术由于具有长距离、快速、可靠、经济且无须剥离外包层等优点，近年来受到国内外无损检测学者的极大关注。

Kwun[1,2]利用磁致伸缩传感器对管道中缺陷进行检测和描述，深入研究了多种特征对象中纵向模态导波的频散特性。金建华[3]研制了基于磁致伸缩效应的导波传感器，讨论了传感器结构设计及结构参数的选择方法。王悦民[4]开发了用于磁致伸缩导波检测的实验系统，验证了磁致伸缩导波检测方法的可行性。任晓可[5]采用ANSYS仿真了电磁超声换能器偏置磁场和钢板内涡流的大小，并得到传感器参数与涡流大小的关系，以此推测产生导波的大小。靳志胜[6]仿真分析了偏置磁场均匀性对电磁超声传感器的影响，并尝试使用压电单元类比磁致伸缩效应中力磁耦合的过程，仿真磁致伸缩效应。万红[7]尝试使用热结构分析模块中的热膨胀效应类比模拟磁致伸缩效应中磁—位移场的相互关系。Lerch[8]提出通过有限元、边界元以及多重网格法对换能器进行建模。Jian和Dixon[9,10]历经多年时间对电磁超声在非磁性材料中的发射与接收进行全面模拟。

但上述研究均以理想构件（非承载）为对象的，未考虑外加应力对检测效果的影响。然而在役设备必然会受到自身残余应力或工作应力的作用，力磁耦合不可避免，尽管在相关研究上取得了许多新的进展，但目前关于外加应力对电磁超声换能器换能效率的影响问题仍然了解得很少，因此深入研究外加应力与磁致伸缩效应的作用关系，解决力磁耦合作用下试件裂纹检测技术的“瓶颈”问题，对缩小我国在裂纹检测、评价方面与国外的差距，具有非常重要的实际意义。

1 力磁耦合作用下外加应力对磁致伸缩应变的影响

根据力—磁—热多场耦合的非线性理想本构模型[11]，如果不考虑温度效应，令∆T=0。则该模型可简化为：

式中，ε为应变，H为作用磁场，λs为饱和磁致伸缩系数，Ms为饱和磁化强度，M为磁化强度，σs为饱和应力，σ为外加应力，χm为初始磁化系数，µ0为真空磁导率，ES为材料的固有杨氏模量。

式(1)中，第一项反映磁致伸缩材料固有的弹性性质，表示材料应变与外加应力间的线性关系；第二项反映由于应力各向异性，磁畴在应力作用下发生转动对其弹性性质(应变)的影响；第三项反映力磁耦合作用对材料弹性性质的影响。

在σ=0条件下，式(2)可简化为：

根据Clark[12]实验结果，磁致伸缩应变仅与磁化M2有关。从式(1)中取第三项，则可得出力磁耦合作用下磁致伸缩应变本构关系。

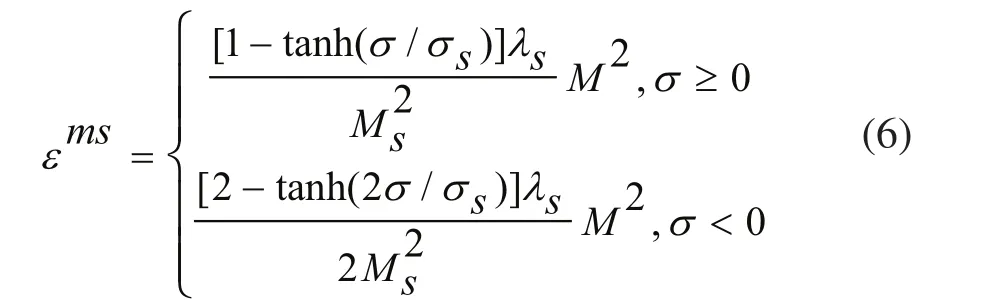
式中，εms为磁致伸缩应变。

将式(5)代入式(6)得:

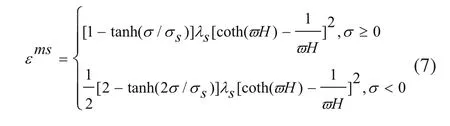
2 电磁超声换能器仿真模型建立

电磁超声换能器激励端由永久磁铁，“回字形”线圈，被检测工件三部分组成，在线圈产生的交变磁场和永磁铁提供的偏置磁场的耦合作用下，被检测工件内产生磁致伸缩效应，最终形成超声振动波。根据电磁超声换能器的结构特征，运用COMSOL Multiphysics有限元分析软件建立电磁超声换能器有限元分析模型，其中激励端几何模型如图1所示。被检钢板材料为Q235钢，长度、宽度和厚度分别为96mm、70mm和6mm，应力及磁特性属性参数如表1所示，材料B-H曲线如图2所示。偏置永磁体几何尺寸及材料属性参数如表2所示。铜制线圈以“回字形”方式缠绕，所加载的输入电流如式(8)所示：

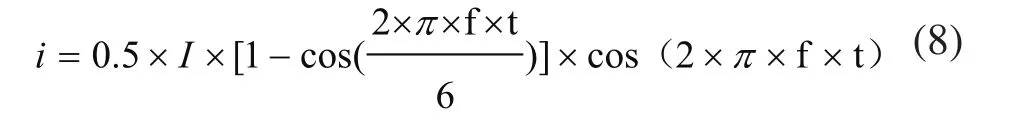
式中I为电流大小，f为激励频率。

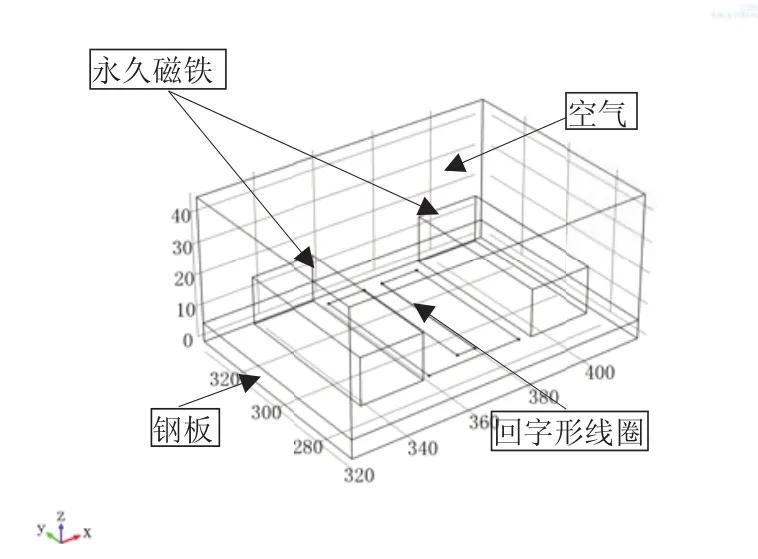
图1 电磁超声换能器几何模型

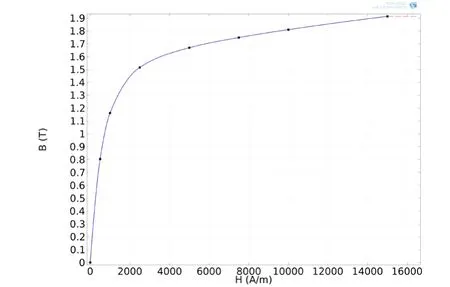
图2 Q235钢BH曲线

3 仿真结果分析

由力磁耦合作用下磁致伸缩材料的本构方程式(7)可知：在待检测工件存在外加应力时，材料的磁致伸缩振动是由外磁场和外应力共同决定的。使用上节建立的仿真模型，依次分析钢板中应力及磁场的分布规律；力磁耦合作用下钢板中磁致伸缩振动的变化规律，并探讨克服外加应力使电磁超声换能器换能效率降低的实际办法。

表1 钢板应力及磁特性属性参数

表2 偏置永磁体几何尺寸及材料属性参数

3.1 钢板中应力及磁场分布

仿真模拟了外加压应力为0～400MPa的11组电磁超声换能器。当外加压应力为20MPa时，钢板应力分布图如图3所示，结果表明：外加应力使材料产生应变，应变导致材料几何尺寸发生变化。钢板内由永磁体提供的静态磁场如图4所示，由线圈提供的动态磁场如图5所示，结果表明：钢板内磁场分布并非均匀的，磁场在永磁体与线圈下方处值较大，而在靠近模型端部处值较小，并且由线圈所产生的磁场较小，远不及永磁体所产生的的磁场，故最终线圈产生的大小与方向时变的动态磁场与永磁体产生的静态偏置磁场耦合作用于钢板，在板内形成一个大小变化但方向不变的动态磁场。

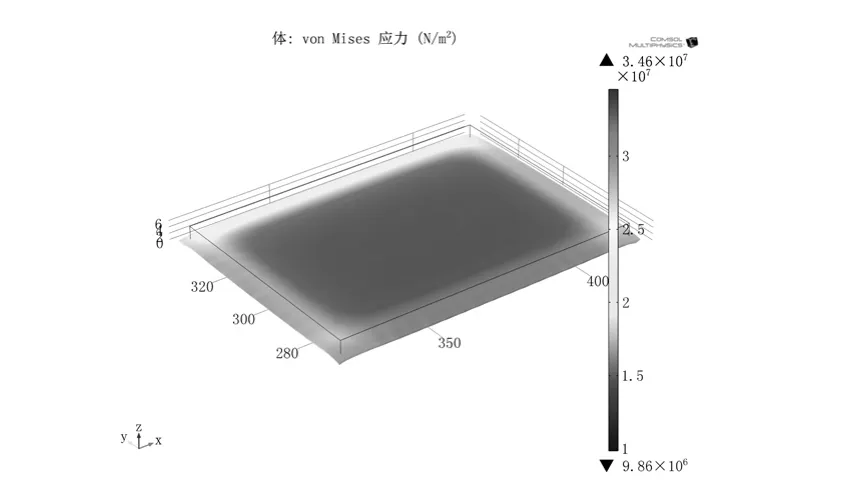
图3 钢板应力分布

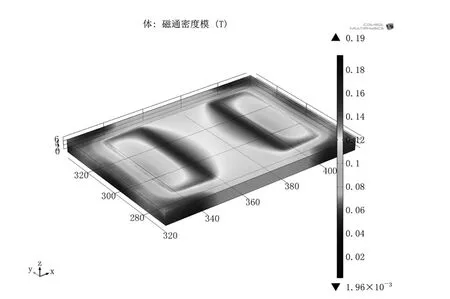
图4 板中由永磁体产生的磁场

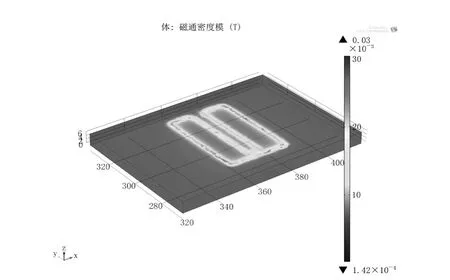
图5 板中由线圈产生的磁场

3.2 力磁耦合作用下钢板中磁致伸缩振动

设置瞬态求解时间为：5.5×10-5(s)，求解步长为：1×10-7(s)，结合力磁耦合作用下磁致伸缩材料本构方程(7)，通过加载求解，读取换能器正下方钢板中心处坐标为(368,300,3)质点的磁致伸缩位移量，如图6所示，并提取图6中磁致伸缩振幅量绘于图7。分析结果表明：在相同激励磁场的条件下，随着外加应力的增加，磁致伸缩振幅减小，换能器换能效率降低，当外加应力值超过材料的屈服强度时，磁致伸缩振幅趋近于零。这是由于：当引入外加应力σ时，由应力引发的各向异性使磁畴难以向磁化方向发生偏转，所以在相同磁场中，磁致伸缩应变随外加应力的增加而逐渐减小。当外加应力值超过材料屈服强度时，材料力学状态近于饱和，故难以被激励出超声振动。

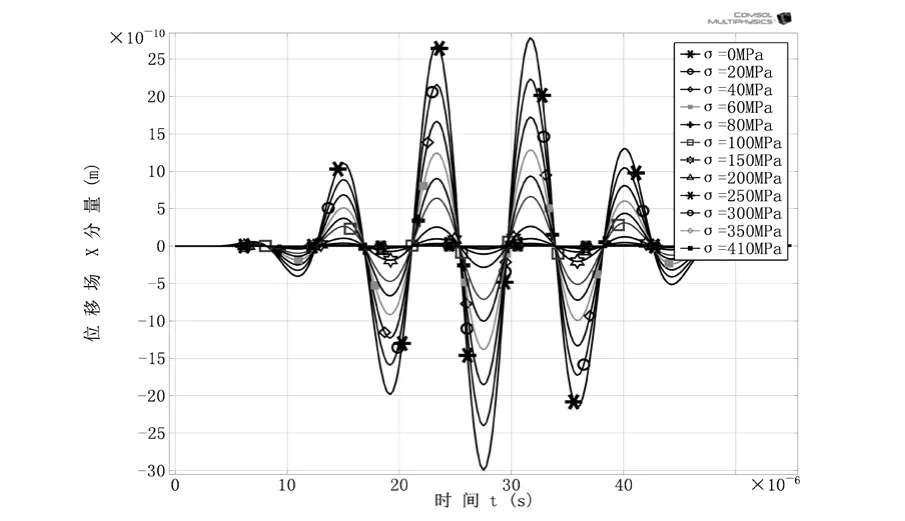
图6 不同外加应力下时间-磁致伸缩振动

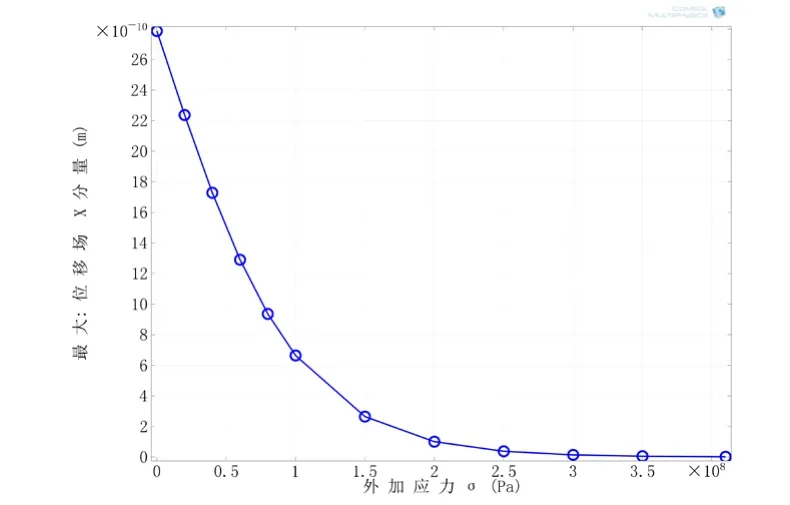
图7 外加应力-磁致伸缩振幅

3.3 电磁超声检测效率提升办法

为了克服外加应力对电磁超声检测效果的影响，尝试增加换能器的激励能量。当同时改变换能器偏置永磁体剩余磁通密度和外加应力时，钢板内质点磁致伸缩振幅量如图8所示；当同时改变换能器线圈激励电流大小和外加应力时，钢板内质点磁致伸缩振幅量如图9所示。分析结果表明：在改变换能器永磁体剩余磁通密度或激励电流大小时，外加应力对换能器换能效率影响趋势不变(即随外加应力增大，换能效率降低)，但随永磁体剩余磁通密度或线圈激励电流大小的增加，钢板内由电磁超声换能器激励产生的超声波能量增大，磁致伸缩振幅增大。因此，当被检测工件存在外加应力导致检测效果降低时，应适当增加电磁超声换能器偏置永磁体剩余磁通密度或增加线圈激励电流大小，以保证较高的电磁超声检测效率。

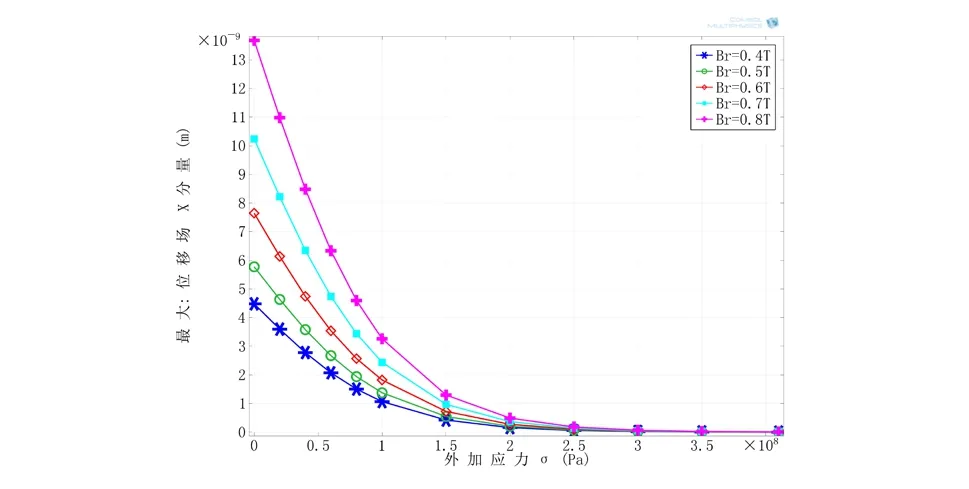
图8 不同永磁体剩余磁通密度下外加应力-磁致伸缩振幅

4 结论

由力—磁—热多场耦合的非线性理想本构模型，推导了力磁耦合作用下磁致伸缩应变本构关系，并由此研究了力磁耦合作用下外加应力对电磁超声换能器换能效率的影响关系，通过理论研究和数值模拟得出以下结论：

1）对于磁致伸缩材料而言，由外加应力引发的各向异性使磁畴难以向磁化方向发生偏转，因此在相同磁场中，磁致伸缩振幅随外加应力的增加而逐渐减小，当外加应力超过材料屈服强度时，磁致伸缩振幅趋近于零。

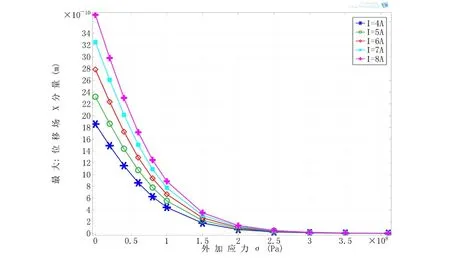
图9 不同线圈激励电流下下外加应力-磁致伸缩振幅

2）随着外加应力的增大，电磁超声换能器换能效率减小，严重影响检测效果。要保证较高的电磁超声换能器换能效率，则需增加换能器中偏置永磁体剩余磁通密度或增加线圈激励电流大小。

[1]H.Kwun,J.J.Hanley,A.E.Holt. Detection of corrosion in pipe using the magnetostrictive sensor technique [J].NDT and E International,1997,30(2):30-33.

[2]H.Kwun, K.A.Bartels, C.Dynes. Dispersion of longitudinal waves propagating in liquid-filled cylindrical shells [J].Journal of the Acoustical Society of American, 1999,105(5):2601-2611.

[3]金建华,金纪东.基于磁致伸缩效应的管道纵向超声导波检测传感器[J].仪表技术与传感器,2004,(11):3-4.

[4]王悦民,康宜华,武新军.基于磁致伸缩效应的钢管缺陷试验研究[J].振动、测试与诊断,2005,34(12):210-213.

[5]任晓可,李健.电磁超声无损检测技术的ANSYS仿真研究[J].电子测量技术,2008,31(7):26-29.

[6]靳志胜.磁致伸缩导波无损检测方法与仿真试验研究[D].武汉:湖北工业大学,2009.

[7]万红,沈仁发,吴学忠.对称磁电层合板磁电转换效应理论研究[J].物理学报,2005,54(3):1426-1430.

[8]R.Lerch, M.Kaltenbacher, H.Landes, et al. Advanced computer modeling of magnetomechanical transducers and their sound fi elds[C].2000 IEEE Ultrasonics Symposium,2000:747-758.

[9]X.Jian, S.Dixon, R.S.Edwards, et al. Coupling mechanism of EMATs for ultrasonic generation[J].The Journal of the acoustical society of America,2006,119(5):2693-2701.

[10]X. Jian, S. Dixon,R. S. Edwards, et al. Coupling Mechanism of an EMAT[J].Ultrasonics, 2006, 44:653-656.

[11]Xiaojing. A nonlinear constitutive model of magnetothermo-mechanical coupling for giant magnetostrictive materials[J].Journal of Applied Physics, 2006,100(6):063906-063906-6.

[12]A.E.Clark. Mafnetostrictive rare earth-Fe2 compounds[J].Wohlforth,E,P.(Ed),Ferromagnetic materials,Vol.1,N North-Holl and Amsterdam,1980:531-589.