基于一个新高分数维混沌系统的彩色图像加密

赵建峰, 王淑英, 张理涛, 李险峰

(1.河南职业技术学院信息工程系,河南郑州450046； 2.黄河科技学院民族学院,河南郑州450053；3.郑州航空工业管理学院数理系,河南郑州450015； 4.香港城市大学土木建筑工程系,香港999077)

在当今信息社会,随着计算机网络技术的飞速发展和微型计算机的普及,越来越多的多媒体数字信息通过网络进行传输,据统计,其中图像信息约占信息总量的70%.这些信息在传输过程中的安全与保密不仅关系到个人隐私、企业的商业机密等问题甚至关系到国家安全,因此在网络中图像信息的安全与保密技术已越来越受到全社会的重视.混沌系统具有良好的伪随机特性、轨道的不可预测性、对系统初值及参数的极端敏感性及拓扑传递性等特点.由于越来越广泛使用的图像和多媒体信息的数据量大且冗余度高,已给传统密码提出了挑战,混沌信号天然的随机性和隐蔽性等诸多特性使混沌成为加密研究的新热点.L.Kocarev[1]将二者之间的一些对比关系做了总结,国内外学者改进加密技术并将混沌动力学应用于传统的加密算法[2-7].而采用一维混沌系统的加密算法,已被证明安全性不高,因为密钥空间不够,不能抵御穷举攻击；且容易利用相空间重构方法进行混沌系统识别[8],攻击者只要截获足够长的明文/密文对,就能够破解种子密钥,从而不能抵御已知明文攻击.为了加强图像加密的安全性,高维混沌加密算法已成为研究热点[9-15].

数字图像像素位置的置乱变换是一种重要的加密方法,不会改变图像的直方图特征,对于冗余度高的图像不太适合,较难应对穷举攻击法,为提高加密性能,与其他加密算法相融合,本文对于彩色图像先进行基于混沌序列的图像R、G、B三基色平面像素置乱,之后对密文三基色分量进行像素值异或替代加密,最后对密文进行统计特性分析.

1 高维数混沌系统

各种混沌系统相继被提出,其中分数维数越高,系统占用的空间就越大,系统的吸引子的缠绕性就越复杂,混沌信号的类随机性越强,而具有高分数维数的混沌系统并不多见[16-17],为此,构造一个新三维自治混沌系统,其方程为

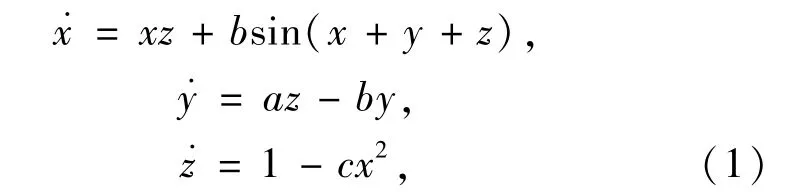
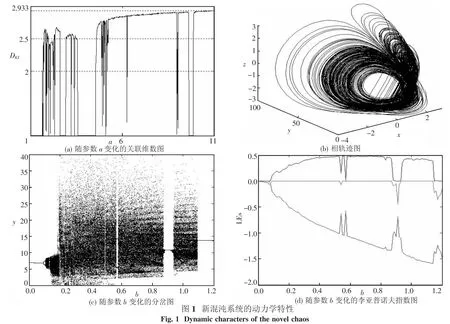
其中,X=(x,y,z)T为系统的状态变量,(a,b,c)T为系统的参数向量.图1(a)给出新混沌的控制参数a在区间[1,11]内连续变化下的DKY值.图1(a)显示,此混沌吸引子的DKY几乎都大于2.5,并且随着控制参数继续增大,有的混沌吸引子的DKY甚至达到了2.933.图1(b)和图1(c)展示了该混沌系统的非线性特征.取积分步长为0.01,在积分5×105次后,计算得出的3个Lyapunov指数分别为(l1,l2,l3)=(0.555 8,0,-0.595 3),DKY=2.933 6,DJ=2.955 1,关联维数D2=2.912 4,DKY和DJ的绝对误差|d|是0.021 4,DKY依旧小于DJ.

令(1)式中各项等于零,得到

求解(2)式中的2个平衡点分别为点M(-0.447 2,-13.416 2,-0.268 3)和点N(0.447 2,-4.085,-0.817 1),在点M处对系统(1)进行线性化,得到系统的Jacobian矩阵为

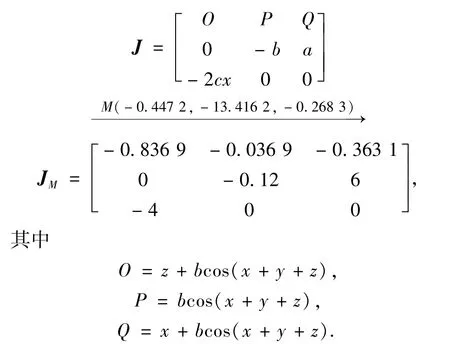
为求出系统(1)在平衡点M处相应的特征值,令det(JM-λI)=0,解得特征值为:λ1=0.353,λ2,3=-0.654 9±1.259 5i.

同理解得平衡点N处的特征值为λ1=0.13,λ2,3=-0.216 8±1.251 3i,可见2个平衡点有1个特征值是正实数,而另外2个是一对共轭复数,因此2个平衡点都是第一类鞍点,显然是不稳定的.由微分方程理论知这2个平衡点都不稳定,其中实部为负的特征根保证平衡点在某方向上有吸引性,使轨线收敛,正特征根保证平衡点在某方向有排斥性,使轨线螺旋发散.这从理论上证明了该系统存在混沌的可能性.

混沌吸引子的相邻轨线呈现分离的趋势,Lyapunov指数图可以定量描述轨线收缩或者开展的量,采用四阶Runge-Kutta算法对系统进行数值仿真,步长根据控制目标进行调整,系统的全局分岔图如图1(c)所示.由此可见,当分岔参数b递增的时候,系统呈现出复杂的动力学行为.系统的全局Lyapunov指数谱如图1(d)所示,与系统的全局分岔图(图1(c))完全吻合.

2 基于新混沌的数字图像加密实现

2.1 算法描述基于混沌的加密流程如图2所示.读入原始图像Ximage,大小为M×N的Lena图像,A(x,y)(x∈[0,M-1],y∈[0,N-1])表示原始图像在点(x,y)处的像素值,Ai(x,y)(x∈[0,M-1],y∈[0,N-1])(i=1,2,3)表示原始图像在第i次加密后的像素值.基于图像像素值替代的加密算法设计如下.

1)给出新混沌的系统参数(a,b,c)和系统初始值(x(0),y(0),z(0))作为密钥,代入混沌系统(1),生成3个混沌序列(x,y,z).计算过程中,使用双精度数以降低出现循环数据的可能性.

2)动力系统初期不会立刻进入混沌状态,故加密时从混沌序列(x,y,z)的第1 000位开始取起,x=reshape(x(1 000:M*N+1 000-1),M,N)；y=reshape(y(1 000:M*N+1 000-1),M,N)；z=reshape(z(1 000:M*N+1 000-1),M,N).

利用排序函数对3个混沌序列进行排序并记下位置矩阵,用位置矩阵对图像的R分量、G分量和B分量分别进行像素位置置换.

3)取x序列中每一个值小数点后的第5、6、7三位数字组成一个正整数进行模运算,将此整数对256取余,得到一个字节的无符号整数:

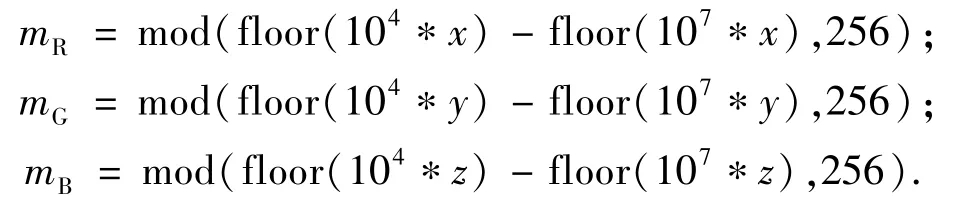
将无符号整数组成加密序列,对置乱图像中的(i,j)位置的像素点的灰度值A(i,j)进行二进制位异或操作得到加密图像.

2.2 数值试验和安全性分析仿真实验以Matlab 7.1为平台,明文图像选用大小分别为256×256的Lena彩色图像,加密效果如图3和图4所示.

相邻像素的相关性.为了检验原始图像和加密图像相邻像素的相关性,从图像中选取1 000对水平方向、垂直方向和对角方向相邻像素对,用如下公式定量计算相邻像素的相关系数:

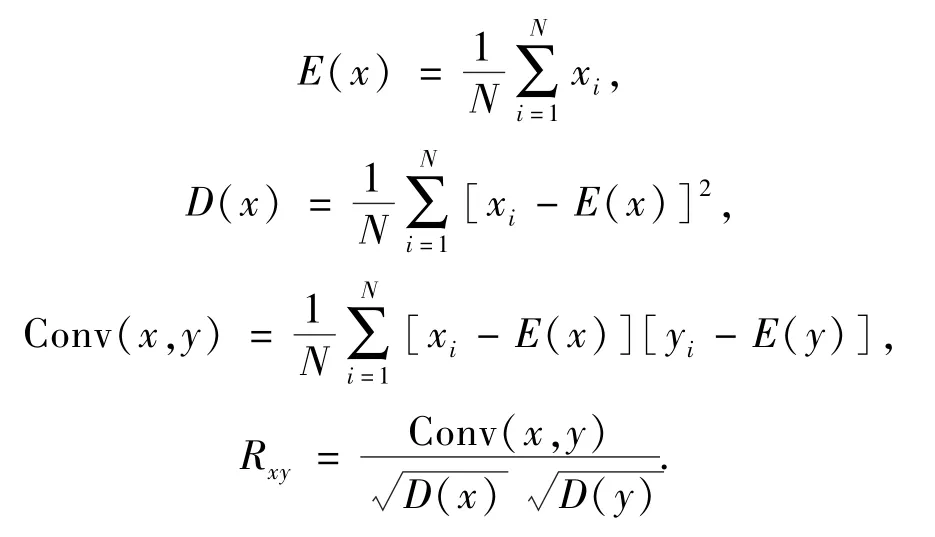
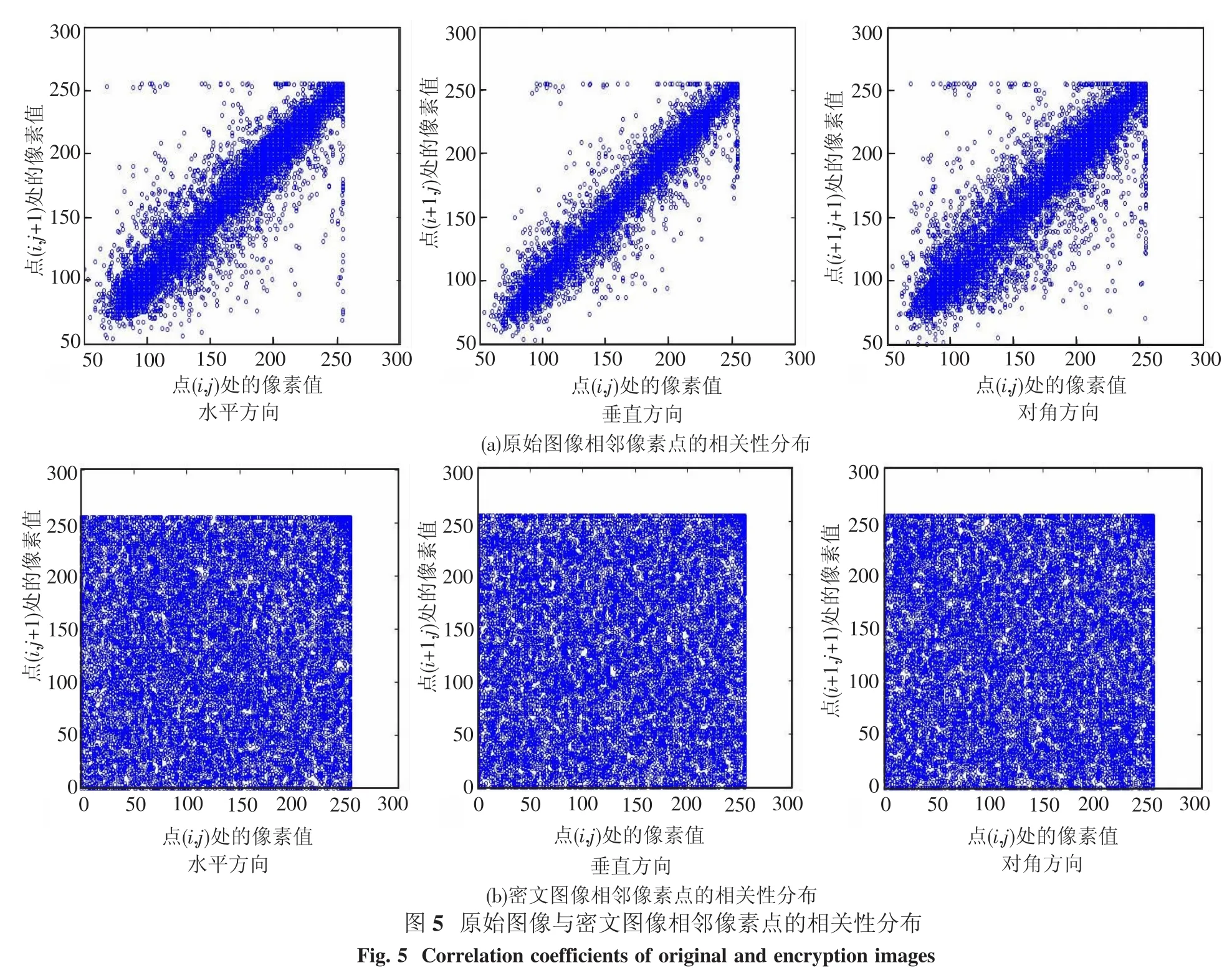
从图5和表1中可以看出,原始图像的相邻像素是高度相关的,而加密图像的相邻像素相关系数已经明显降低,原始图像的统计特性已经扩散到随机的密文中.

表1 原始图像和密文图像相邻像素的相关性系数分析Table 1 Correlation coefficients of original and encryption image

3 结论

本文提出一个彩色图像加密算法,先通过新的最复杂吸引子产生的3个混沌序列生成位置矩阵对R、G、B三基色进行位置置乱,生成置乱图像.为增强加密效果,再利用3个混沌序列对置乱图像的三基色平面进行异或加密,直方图显示加密效果良好,并且相邻像素的相关性极大降低,Matlab平台数值仿真给出了3个方向的相邻像素相关系数及图像,验证了此算法的适用性.

[1]Kocarev L.Chaos-based cryptography:a brief overview[J].IEEE Circuits and Systems,2001,1(3):6-21.

[2]Chen G R,Mao Y B,Chui C K.A symmetric image encryption scheme based on 3D chaotic cat maps[J].Chaos Solitons and Fractals,2004,21(3):749-761.

[3]廖晓峰,肖迪,陈勇,等.混沌密码学原理及其应用[M].北京:科学出版社,2009.

[4]杨小平,付静.一种混沌密码体制的实现[J].四川师范大学学报:自然科学版,2004,27(4):431-433.

[5]庞朝阳,周日贵,丁从宝,等.量子算法及其在图像处理中的应用[J].四川师范大学学报:自然科学版,2009,32(4):522-540.

[6]Ismail A I,Mohammed A,Hossam D.A digital image encryption algorithm based a composition of two chaotic logistic maps[J].Int J Network Security,2010,11(1):1-10.

[7]赵耿,李杨,方锦清.电子商务中混沌密码算法的研究[J].广西师范大学学报:自然科学版,2005,23(4):1-7.

[8]王雅庆,周尚波.基于分数阶陈氏混沌系统的图像加密算法[J].计算机应用,2013,33(4):1043-1046.

[9]靳冰,祝孔涛.基于小波和混沌的图像置乱加密新算法[J].西华大学学报:自然科学版,2012,31(6):44-45.

[10]Behnia S,Akhshani A,Mahmodi H,et al.A novel algorithm for image encryption based on mixture of chaotic maps[J].Chaos Solitons and Fractals,2008,35(2):408-419.

[11]Gao T G,Chen Z Q.A new image encryption algorithm based on hyper-chaos[J].Phys Lett,2008,372(4):394-400.

[12]韩凤英,朱从旭.基于Lorenz系统的自适应数字图像加密算法[J].吉首大学学报:自然科学版,2011,32(4):39-41.

[13]Seyedzadeh S M,Mirzakuchaki S.A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map[J].Signal Processing,2012,92(5):1202-1215.

[14]曾光辉,胡凯,佟维.基于Logistic均匀分布图像置乱方法[J].物理学报,2011,60(11):11508-1-8.

[15]朱从旭,孙克辉.对一类超混沌加密算法的密码分析与改进[J].物理学报,2012,61(12):120503-1-11.

[16]高智中,韩新风,章毛连.一个新的混沌系统及其电路仿真[J].四川师范大学学报:自然科学版,2012,35(2):288-292.

[17]褚衍东,李险峰,张建刚,等.一类新自治混沌系统的计算机仿真与电路模拟[J].四川大学学报:自然科学版,2007,44(3):550-556.