基于高精度波前快速推进法的页岩气储层动用分析

黄世军，滕柏路，程林松，艾 爽，贾 振

（中国石油大学（北京）石油工程学院，北京 102249）

基于高精度波前快速推进法的页岩气储层动用分析

黄世军，滕柏路，程林松，艾 爽，贾 振

（中国石油大学（北京）石油工程学院，北京 102249）

为了快速准确模拟页岩气储层开发过程中的动用情况，利用高精度波前快速推进法对波前运移程函方程进行求解，通过复合线性流模型对多级压裂水平井模型中的气体流态进行分区，实现飞行时间与真实时间的换算，得到储层动用随时间变化示意图及储层动用范围与时间的定量关系.对比波前快速推进法与高精度波前快速推进法的计算结果，发现在相同时间内，利用高精度波前快速推进法计算时储层动用范围更大.在裂缝总长相等的情况下，通过对比不同裂缝形态下的储层动用发现，在裂缝间的压力达到连通前，储层动用程度与裂缝形态无关；当裂缝之间压力连通后，储层动用与裂缝形态密切相关.

页岩气；高精度波前快速推进法；储层动用；波前运移；裂缝形态

0 引言

随着钻井及压裂技术的进步，页岩气藏得以经济高效的开采，页岩气也成为北美地区主要的供气来源，北美页岩气的成功开发也激起全球开采页岩气的高潮[1-2].中国具有丰富的页岩气资源，经济价值巨大，加大对页岩气的开发力度可以有效缓解能源紧张的局势[3-7].在页岩气藏生产过程中，储层动用范围是描述页岩气藏生产能力的一个重要参数，大部分研究人员认为压裂改造区（SRV）外侧的动用很少.Fisher M K等利用微地震监测技术研究Barnett页岩压裂水平井的裂缝分布情况[8]，Mayerhofer M J等阐述从微地震图数据估算SRV的方法，实现利用微地震监测技术研究页岩气藏压裂水平井动用规律[9].徐兵祥等利用双孔瞬态线性流动模型及典型生产曲线，分析Eagle Ford页岩气藏产量数据，计算压裂区范围内的游离气总储量，从而得到SRV[10].这些研究只是静态地利用SRV表征储层的动用情况，并没有动态给出储层动用范围随时间的变化，更没有考虑到开发后期改造区以外的储层动用.另外，虽然可以采用Eclipse等数模软件模拟储层的动用变化，但在模型网格数较多的情况下，一般数模软件需要花费几十分钟甚至几个小时才能完成模拟运算.Jiang Xie等提出利用波前快速推进法（简称FMM）预测储层动用范围的方法，即使针对百万计网格的计算也只需要十几分钟时间[11-12].在利用FMM进行计算时，由于插值方法所限，所得结果的精度还有待提高.

笔者改变FMM的插值计算方法，利用高精度波前快速推进法（简称HAFMM）模拟计算波前运移情况，实现对储层动用范围随时间变化更为准确的预测，并且对比不同裂缝形态下的储层动用结果，对页岩气藏的生产开发具有指导作用.

1 波前运移程函方程

超低渗是页岩气藏的一个重要特点，与常规气藏相比，压力波不可能在短时间内传到整个储层，相反，在整个气藏的开发过程中，储层的压力传播往往限制在距离井筒不远的范围内.对于气藏，压力波传播的范围即代表储层动用的范围.为了对页岩气井产能及气藏开发状况进行准确快速的预测，对波前运移的研究显得更为重要.文中对于压力波前缘的预测主要基于调查半径，Lee W J提出调查半径的概念，并给出调查半径r的计算公式[13]：

式中：K为渗透率；t为时间；φ为孔隙度；μ为气体黏度；ct为综合压缩系数.通常，对于不同的流动模型，压力波传播的距离和时间关系可以写为，其中η=K/（μφct），β是与流态有关的常数，在线性流、平面径向流及球面径向流中取值分别为2、4、6[14].波前运移的程函方程可以写为

其中，未知量τ（x）为飞行时间，它与波的传播时间t有关，即

在将飞行时间换算成真实时间时，利用Van Kruysdijk等提出的多段压裂水平井的复合线性流模型[15]（见图1），将区域分为4个流态：（1）裂缝线性流；（2）双线性流；（3）复合线性流；（4）拟径向流.在换算过程中β在不同区域分别选取相应的值.

基质和裂缝的程函方程可以分别写为

图1 复合线性流模型Fig.1 Compound linear flow model

式中：下标m、f分别代表基质与裂缝系统，其中ηm=Kami/（μgiφmctmi），ηf=Kf/（μgiφfctfi）.

Kami是在考虑滑脱、扩散情况下基质的原始表观渗透率[16]，即

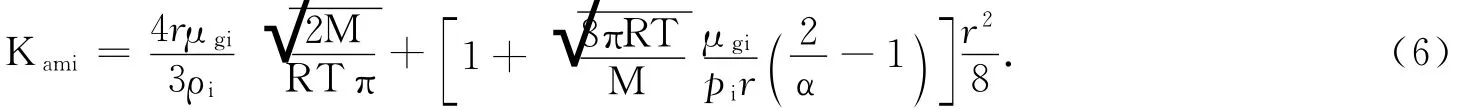
ctmi是考虑解吸条件下基质的原始综合压缩系数，即

ctfi是裂缝的原始综合压缩系数，即

式（6-8）中：r为基质孔隙半径；ρi为气体原始密度；M为储层气体的相对分子质量；R为通用气体常数；T为储层温度；pi为储层原始压力；α为切向动量供给因数，取为0～1；cmi为基质系统原始压缩系数；cfi为裂缝系统原始压缩系数；cgi为气体原始压缩系数；cdi为基质原始解吸压缩系数.

2 利用HAFMM求解程函方程

2.1 计算方法

HAFMM是Sethian J A提出的可以高效计算程函方程的一种方法[17]，利用HAFMM求解计算波前运移的程函方程，可以对储层动用进行预测.利用HAFMM计算时用到的点见图2.

假设 点τi，j未 知，它 周 围 的 8 个 点τi，j+1、τi，j-1、τi+1，j、τi-1，j、τi，j+2、τi，j-2、τi+2，j、τi-2，j是已知的，Sethian J A 提出计算τi，j方法，则

由式（2）可得

图2 波前快速推进法中的相邻点Fig.2 Neighborhood points in FMM

将式（10）代入式（9），可以得到η，即

式（11）中，差分运算D的计算方法[18]为

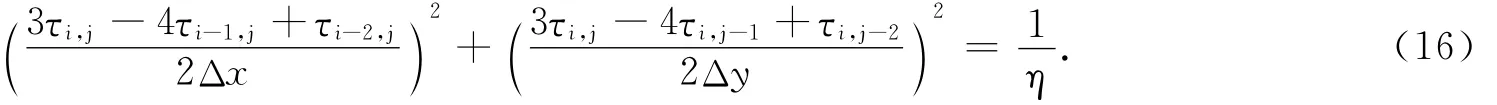
式（16）是一个简单的一元二次方程，对其求解，选出较大的解作为τi，j值.当τi，j周围的8个点中，如果有任意点值不为已知，在计算τi，j时可不将其考虑在内.

2.2 计算过程

HAFMM的计算过程见图3：

（1）找到所有的已知点标记为初始点，见图3（a）中的黑点；（2）找到初始点周围的相邻点，并利用初始点计算相邻点的值，标记为备选点，见图3（b）中的蓝点；（3）选出所有备选点中的最小值，标记为已知点，见图3（c）红框中的点，并以它为初始点计算相邻点的值，标记为备选点，见图3（d）；（4）重复步骤（2）和（3），直到所有点被标记为已知点.

式（12-15）中：Δx、Δy分别代表x、y方向上两点间的距离.在x方向上，比较、、0的大小，选出最大值，确保压力波沿x方向一直向外推进，假设为τ，同理也选出y方向的最大值，假设为τ，式（11）可以改写为

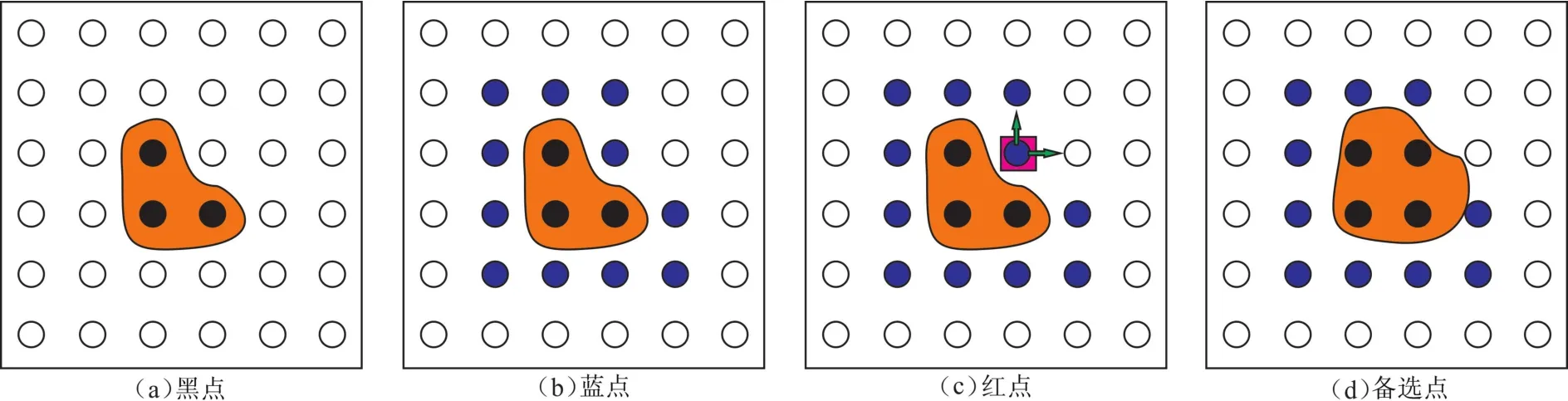
图3 HAFMM计算过程Fig.3 Calculation process of HAFMM

3 结果分析

3.1 参数选取

综合文献[16，19]，在计算页岩气藏压力波前缘运移情况时，选用的参数见表1.

在计算基质表观渗透率时，考虑基质孔隙的吸附作用，在基质的孔隙壁上吸附一层分子膜，所以在计算时，需要使用基质的有效孔隙半径re，re=rm-2rg，其中，rm为基质孔隙半径；rg为气体半径.

将re代入到式（6）中，可以得到基质的表观渗透率Kami=5.21×10-6μm2.

3.2 HAFMM与FMM结果对比

与传统的 FMM 不同，HAFMM 改变 FMM 中的一阶近似插值方法（τi+1，j-τi，j）/Δx，替换成二阶近似，使得所计算的结果更加准确.为了比较 HAFMM 与FMM 的计算结果，选用裂缝模型（见图4），其中中水平井长度L=1 000 m，裂缝长度Lf=500 m，裂缝间距为200 m.

表1 储层参数Table 1 Reservoir parameters

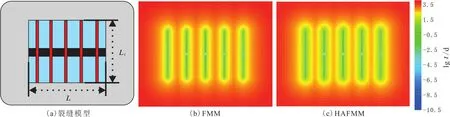
图4 裂缝模型及HAFMM与FMM计算的动用范围随时间变化结果Fig.4 Fracture model and drainage area vs time under FMM and HAFMM

储层动用范围与时间的关系曲线见图5（其中箭头所指处代表裂缝间的压力达到连通）.由图4及图5可以看出，利用HAFMM计算时，在相同的时间内储层动用的范围比利用FMM计算传播的范围更大.以气井生产3 a为例，利用HAFMM计算时储层的动用范围为0.823 km2，比利用FMM的计算结果0.779 km2要多出0.044 km2；当气井的生产时间达到12 a时，前者的计算结果为1.402 km2，后者的计算结果为1.33 km2，两者相差0.072 km2，且随着生产时间的增加，两者的差别越来越大.

3.3 不同裂缝形态下的储层动用

在页岩气藏开发的过程中，裂缝的形态对气井产能具有直接影响.在裂缝总长度相等的条件下，考虑缝间干扰对储层动用的影响及工程施工的可行性，选取5种裂缝形态进行对比（见表2）.其中裂缝间距为200 m，并且假设气井生产过程中未受到边界的影响.

经HAFMM计算的结果见图6.图6的橙色、紫色和粉色区域分别代表气井生产30 d、2 a和9 a时储层的动用范围.压力波的传播范围与时间的关系曲线见图7.

由图7可以看出，当气井生产570 d时，裂缝之间的压力达到连通，5种裂缝形态下的储层动用范围为0.681 km2，在此之前储层动用范围与裂缝形态无关.这是因为当裂缝之间的压力达到连通之前，各裂缝之间不存在干扰.当裂缝之间的压力达到连通后，不同的裂缝形态下储层动用具有明显区别.在表2（d）时储层动用的最快，表2（e）的动用速度要低于表2（d）的，但明显高于其他3种情况，表2（b）和（c）的储层动用较慢，表2（a）的最慢.这是因为在压力连通后，裂缝之间正对的区域形成严重的干扰区，阻碍压力波的运移.由于在表2（a）时各裂缝长度相等，缝间正对面积达到0.4 km2，干扰区面积最大，所以储层动用最慢.表2（b）和（c）分别采用纺锤型和哑铃型裂缝形态，长短裂缝依次排列，缝间正对面积为0.32 km2，一定程度上减少干扰区的面积，所以它们的动用速度稍快.表2（d）和（e）采用长裂缝与短裂缝交错排列的办法，可有效地将缝间正对面积分别降到0.16 km2和0.24 km2，所以表2（d）的动用最快，表2（e）的次之.

图5 不同算法的储层动用与时间关系曲线Fig.5 Curve of drainage area vs time under different calculation method

表2 裂缝形态与长度Table 2 Fracture pattern and length

图6 不同裂缝形态下的气井生产30 d、2 a及9 a时的储层动用Fig.6 Drainage area after 30 d，2 years and 9 years under different fracture patterns

图7 不同裂缝形态的储层动用与时间关系曲线Fig.7 Curve of drainage area vs time under different fracture patterns

4 结论

（1）利用波前快速推进法对页岩气储层的波前运移进行预测，并且给出储层动用情况与时间之间的定量关系.

（2）对比波前快速推进法与高精度波前快速推进法的结果，利用高精度波前快速推进法计算时，在相同时间内，储层动用范围更大.

（3）选取5种不同的裂缝形态进行对比，在裂缝之间的压力达到连通前，储层的动用与裂缝形态无关；当裂缝之间的压力达到连通后，不同的裂缝形态对储层动用具有明显的影响.

（4）对比不同裂缝形态下的储层动用情况，缝间正对面积越小，即缝间干扰越小，储层动用的越快.

[1] Nobakht M，Clarkson C R.Hybrid forecasting methods for multi-fractured horizontal wells：EUR sensitivities[C].SPE 153220，2012.

[2] Cipolla C L，Lolon E，Mayerhofer M J.Reservoir modeling and production evaluation in shale-gas reservoirs[C].SPE 13185，2009.

[3] 孙赞东，贾承造，李相方，等.非常规油气勘探与开发[M].北京：石油工业出版社，2011：865-1116.

Sun Zandong，Jia Chengzao，Li Xiangfang，et al.Unconventional oil and gas exploration and development[M].Beijing：Petroleum Industry Press，2011：865-1116.

[4] 单衍胜，张金川，李晓光，等.辽河盆地东部凸起太原组页岩气聚集条件及有力预测[J].大庆石油学院学报，2012，36（1）：1-7.

Shan Yansheng，Zhang Jinchuan，Li Xiaoguang，et al.Shale gas accumulation factors and prediction of favorable area Taiyuan formation in Liaohe eastern uplift[J].Journal of Daqing Petroleum Institute，2012，36（1）：1-7.

[5] 梁超，姜在兴，郭岭，等.陆棚相黑色泥岩发育特征、沉积演化及页岩气勘探前景——以瓮安永和剖面牛蹄塘组为例[J].大庆石油学院学报，2011，35（6）：13-21.

Liang Chao，Jiang Zaixing，Guo Ling，et al.Characteristics of black shale，sedimentary evolution and shale gas exploration prospect of shale face taking Weng'an Yonghe profile Niutitang group as an example[J].Journal of Daqing Petroleum Institute，2011，35（6）：13-21.

[6] 久凯，丁文龙，黄文辉，等.渤湾地盆地济阳拗陷沙三段页岩气地质条件分析[J].大庆石油学院学报，2012，36（2）：65-70.

Jiu Kai，Ding Wenlong，Huang Wenhui，et al.Analysis of geological condition of the formation of Shahejie shale gas in Jiyang depression in Bohai bay basin[J].Journal of Daqing Petroleum Institute，2012，36（2）：65-70.

[7] 任俊杰，郭平，王德龙，等.页岩气藏压裂水平井产能模型及影响因素[J].东北石油大学学报，2012，36（6）：76-81.

Ren Junjie，Guo Ping，Wang Delong，et al.Productivity model of fractural horizontal wells in shale gas reservoir and analysis of influential factors[J].Journal of Northeast Petroleum University，2012，36（6）：76-81.

[8] Fisher M K，Heinze J R.Optimizing horizontal completion techniques in the Barnett shale using microseismic fracture mapping[C].SPE 2004，26-29.

[9] Mayerhofer M J，Lolon E P，Warpinski N R，et al.What is stimulated reservoir volume[C].SPE 119890，2008.

[10] 徐兵祥，李相方.页岩气产量数据分析方法及产能预测[J].中国石油大学学报：自然科学版，2011，37（3）：120-125.

Xu Bingxiang，Li Xiangfang.Production data analysis and productivity forecast of shale gas reservoir[J]. Journal of China University of Petroleum：Natural Science Edition，2011，37（3）：120-125.

[11] Zhang Yanbin，Yang Changdong，King Michael J，et al.Fast marching methods for complex grids and anisotropic permeabilities：Application to unconventional reservoirs[C].SPE 163637，2013.

[12] Jiang Xie，Neha Gupta，Michael J King，et al.Depth of investigation and depletion behavior in unconventional reservoirs using fast marching methods[C].SPE 154532，2012.

[13] Lee W J.Well Testing[M]∥Richardson.SPE Textbook Series.Texas：Society of Petroleum Engineers，1982.

[14] Kim J U，Data-Gupta A，Brouwer R，et al.Calibration of high-resolution reservoir models using transient pressure data[C].SPE 124834，2009.

[15] Van Kruysdijk，Dullaert G M.A boundary element solution of the transient pressure response of multiple fractured horizontal wells[C].Cambridge：Paper Presented at The 2nd European Conference of The Mathematicsof Oil Recovery，1989.

[16] Shabro V，Torres-Verdin C，Sepehrnoori K.Forecasting gas production in organic shale with the combined numerical simulation of gas diffusion in kerogen，Langmuir desorption from kerogen surfaces，and advection in nanopores[C].SPE 159250，2012.

[17] Sethian J A.Level set methods and fast marching methods[M].Cambridge：Cambridge University Press，1999：86-100.

[18] Andreas Barentaen J.On the implementation of fast marching methods for 3d lattices[C].Department of Mathematical Modeling，2001.

[19] 王瑞，张宁生，刘晓娟，等.考虑吸附和扩散的页岩是渗透率及其与温度、压力之关系[J].西安石油大学学报：自然科学版，2013，28（2）：50-53.

Wang Rui，Zhang Ningsheng，Liu Xiaojuan，et al.Apparent permeability of shale considering the adsorption and diffusion of gas and the effects of temperature and pressure on it[J].Journal of Xi'an Shiyou University：Natural Science Edition，2013，28（2）：50-53.

TE332

A

2095-4107（2014）04-0017-06

2013-10-12；

陆雅玲

国家“973”重点基础研究发展计划项目（SQ2012CB027805）

黄世军（1974-），男，博士，副教授，主要从事油气渗流机理方面的研究.

DOI 10.3969/j.issn.2095-4107.2014.04.003