奇异非线性二阶边值问题的正解

田淑杰，高 伟，赵冬霞，支 艳

（1.东北石油大学 数学与统计学院，黑龙江 大庆 163318； 2.大庆师范学院 数学科学学院，黑龙江 大庆 163712；

3.中国石油天然气管道局 北戴河培训中心，河北 秦皇岛 066100）

奇异非线性二阶边值问题的正解

田淑杰1，高 伟1，赵冬霞2，支 艳3

（1.东北石油大学 数学与统计学院，黑龙江 大庆 163318； 2.大庆师范学院 数学科学学院，黑龙江 大庆 163712；

3.中国石油天然气管道局 北戴河培训中心，河北 秦皇岛 066100）

利用Schauder不动点定理、截断技术，结合Green函数性质，证明一类奇异非线性二阶边值问题的正解存在性.

二阶奇异边值问题；不动点；正解

0 引言

随着微分方程边值问题理论的不断发展与完善，具有奇异性边值问题的应用前景也逐渐广泛，如大气对流、边界层流动、天体运动和流体力学等，因此具有奇异性的微分方程边值问题的正解存在性的研究成为重要的研究方向之一.近年来，常微分方程边值问题的正解存在性和惟一性研究已有成果.非奇异的情况下，Yao Q L、胡金燕等给出一类二阶非线性周期边值问题存在正解的条件[1-2]；魏淑惠等讨论一类二阶非线性边值问题的正解存在惟一性问题[3]；在具有奇异性的条件下，Jiang D Q、孙经先等研究两类典型的奇异边值问题的正解存在性问题[4-5]；Khan R A、Liu B M等研究两种不同类型的多点奇异边值问题的正解存在性充分条件[6-7]；张国伟研究一类奇异两点边值问题的正解存在性条件[8]；Zhang Z X等研究奇异二阶非线性微分方程周期边值问题的多个正解存在性[9]；刘继颖等给出偶数阶非线性微分方程边值问题的正解存在惟一性结果[10].文献[3]虽然研究含有两个参数的二阶非线性边值问题，并得出正解存在惟一性结果，但未考虑具有奇异性的情形，在f（t，u）于t=0和t=1处为奇异的情况下，笔者研究边值问题的正解存在性问题，证明边值问题的正解存在性和惟一性.

1 边值问题与主要定理

二阶非线性边值问题

式中：α，β为参数，满足α2＞4β＞0.

假设：

（H1）对每个固定的u∈[0，+∞），f（t，u）在[0，1]上非负可积，并且

（H2）对几乎所有的t∈[0，1]，f（t，u）关于u≥0单调非增，并且

在假设（H1）、（H2）条件下，允许f（t，u）具有适当的奇性，称函数u（t）为边值问题（1）的一个正解，如果它满足

定理 假设（H1）、（H2）成立，则边值问题（1）存在惟一的正解.

2 等价形式及Green函数

微分方程

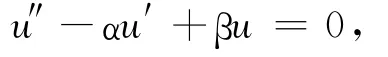
的通解形式为

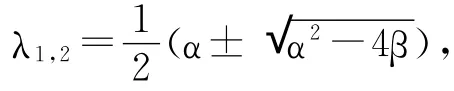
其中再利用常数变异法可得

因此有

利用边值条件u（0）=u（1）=0得

将C3，C4表达式代入式（2）有

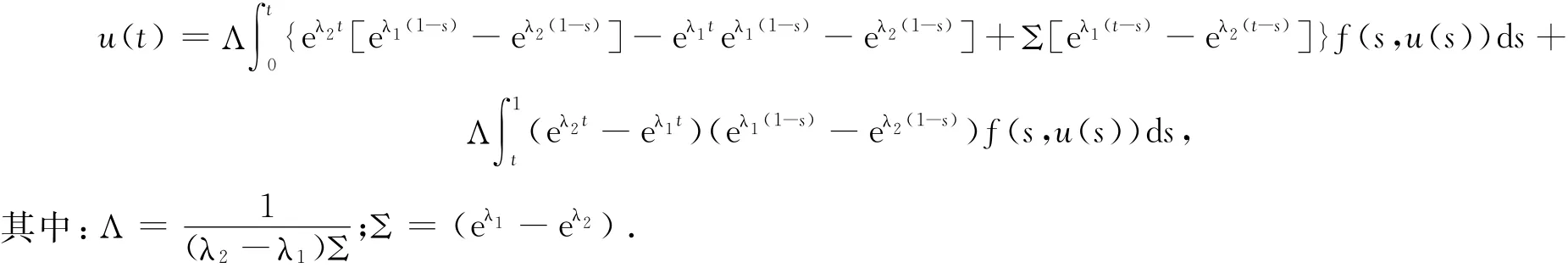
注意到α2＞4β＞0，边值问题（1）等价于积分方程：

式中：G（t，s）为 Green函数，

3 正解存在性及惟一性

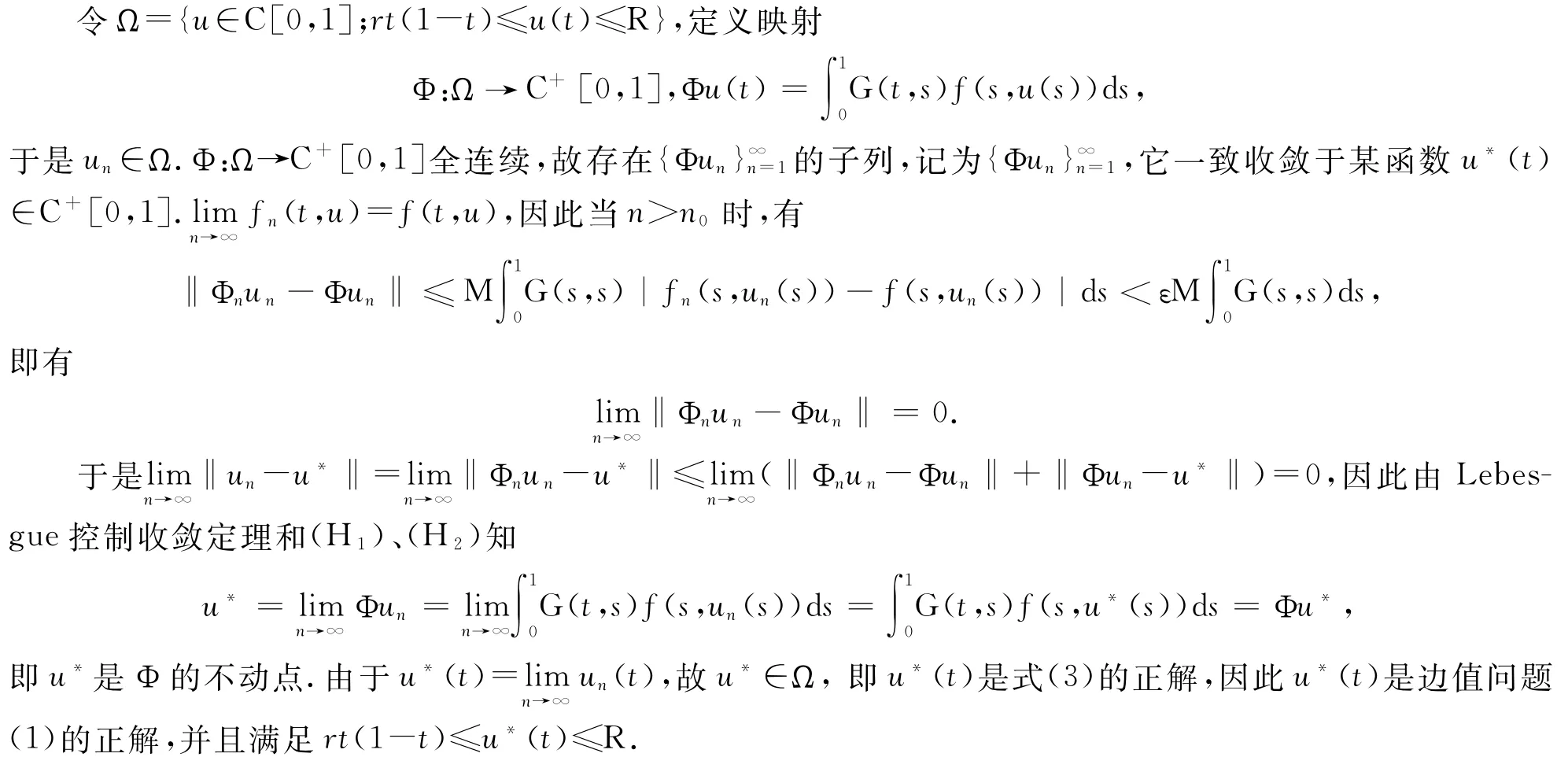
最后证明边值问题（1）的正解惟一性.设u1（t）、u2（t）是边值问题（1）的正解，令

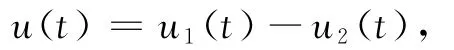
则u（t）满足

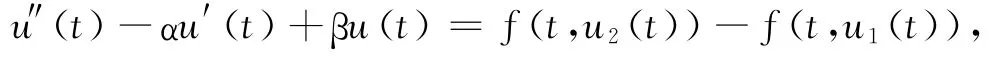
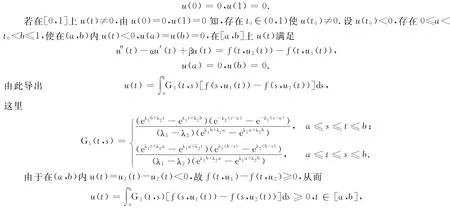
特别u（t0）≥0，与u（t0）＜0矛盾，故u（t）=0，即边值问题（1）的正解是惟一的.

4 结束语

研究一类含有两个参数的二阶非线性边值问题，通过给出问题的Green函数，利用Green函数的性质将边值问题转化为等价的积分方程形式，利用截断技术及Schauder不动点定理，证明正解的存在性和惟一性.

[1] Yao Q L.Positive solutions of nonlinear second order periodic boundary value problem[J].Appl.Math.Letters，2007（20）：583-590.

[2] 胡金燕，孔令彬.二阶非线性周期边值问题的正解[J].大庆石油学院学报，2011，35（5）：97-101.

Hu Jinyan，Kong Lingbin.Positive solutions to a second order periodic boundary value problem[J].Journal of Daqing Petroleum Institute，2011，35（5）：97-101.

[3] 魏淑惠，孔令彬.非线性二阶边值问题正解[J].大庆石油学院学报，2011，35（4）：113-116.

Wei Shuhui，Kong Lingbin.Positive solution to the nonlinear second order boundary value problem[J].Journal of Daqing Petroleum Institute，2011，35（4）：113-116.

[4] Jiang D Q，Chu J，Regan D O'，et al.Multiple positive solutions to superlinear periodic boundary value problems with repulsive singular force[J].J.Math.Anal.Appl.，2003（286）：563-576.

[5] 孙经先，张国伟.奇异非线性Sturm-Liouville问题的正解[J].数学学报，2005，48（6）：1095-1104.

Sun Jingxian.Positive solutions of singular nonlinear sturm-liouville problems[J].Acta Mathematica Sinica，2005，48（6）：1095-1104.

[6] Khan R A.Positive solutions of four point singular boundary value problems[J].Appl.Math.Comput.，2008（201）：762-773.

[7] Liu B M，Liu L S，Wu Y H.Positive solutions for a singular second order three point boundary value problem[J].Appl.Math.Comput.，2008（196）：532-541.

[8] 张国伟，孙经先.一类奇异两点边值问题的正解[J].应用数学学报，2006，29（2）：297-309.

Zhang Guowei，Sun Jingxian.Positive solutions of a class of singular two-point boundary value problems[J].Acta Mathematicae Applicatae Sinica，2006，29（2）：287-309.

[9] Zhang Z X，Wang J Y.On existence and multiplicity of positive solutions to periodic boundary value problems for singular nonlinear second order differential equations[J].J.Math.Anal.Appl.，2003（281）：99-107.

[10] 刘继颖，孔令彬.偶数阶非线性奇异值边值问题正解的存在惟一性[J].大庆石油学院学报，2010，34（2）：113-116.

Liu Jiying，Kong Lingbin.Existence and uniqueness of the positive solution for a even-order nonlinear singular boundary value problems[J].Journal of Daqing Petroleum Institute，2010，34（2）：113-116.

O175.8

A

2095-4107（2014）04-0001-04

2014-03-13；

任志平

黑龙江省教育厅科技项目（12541089）

田淑杰（1979-），女，硕士，讲师，主要从事非线性微分方程边值问题方面的研究.

DOI 10.3969/j.issn.2095-4107.2014.04.001