河道型低渗透储层有限导流垂直裂缝井动态特征

王家航，侯晓春，王晓冬，王 磊，董文秀，李 磊

（1.中国地质大学（北京） 能源学院，北京 100083；2.中国地质大学（北京）能源学院非常规天然气能源地质评价与开发工程北京市重点实验室，北京 100083）

河道型低渗透储层有限导流垂直裂缝井动态特征

王家航1，侯晓春1，王晓冬1，王 磊1，董文秀2，李 磊1

（1.中国地质大学（北京） 能源学院，北京 100083；2.中国地质大学（北京）能源学院非常规天然气能源地质评价与开发工程北京市重点实验室，北京 100083）

低渗透储层内考虑启动压力梯度的流体渗流过程中，动边界的传播规律反映储层的动用范围，并影响井底压力动态.建立河道型低渗储层考虑启动压力梯度和存在动边界的有限导流垂直裂缝井双线性流渗流数学模型，通过Laplace变换，得到动边界传播方程和地层流体压力分布方程；在Laplace变换域中，运用牛顿迭代和Stehfest数值反演方法计算获得井底压力分布特征、动边界传播规律及产能动态曲线.结果表明：启动压力梯度越大，动边界传播越慢、压力损失越大、井产量下降越快；定产条件下，裂缝导流能力越大，压力损失越小；裂缝导流能力对动边界传播影响较小；定压条件下，动边界存在最大值.由压力分布特征和动边界范围确定单井最大动用面积，对实际生产具有指导意义.

启动压力梯度；动边界；有限导流垂直裂缝；双线性流动；压力分析

0 引言

通过对低渗透储层中油气井进行压裂而形成垂直裂缝，可改变近井地层流体渗流方式，提高地层能量的利用率和动用面积[1].低渗透储层渗流规律特殊，通常需要考虑启动压力梯度和动边界传播等非线性渗流问题，分析求解比较复杂.

在低渗透储层中，对考虑启动压力梯度的不稳定渗流问题的分析和求解非常复杂.Prats M[2-3]、刘慈群[4-6]、邓英尔[7-8]等将裂缝抽象为一个细长椭圆，并采用椭圆坐标建立不稳态渗流数学模型.椭圆坐标数学模型的精确求解采用Mathieu方程和周期Mathieu函数，计算过程繁琐，不易完成；考虑启动压力梯度，进一步增加控制方程组的非线性，刘慈群等[4-6]利用影响椭圆近似求解该问题取得较好效果.对于有限导流垂直裂缝井的不稳态渗流分析，采用双线性流动[9]或三线性流动模型[10]，可避免求解地层流动和裂缝流动的耦合积分方程而得到近似解.模型对于泄流面积较大、几何形状较为规则的储层，近似解能够以解析形式给出早期线性流动情况，不能给出中期径向流动情况.考虑一种河道型低渗透储层，该储层—水力裂缝系统可由双线性流动模型模拟.通过改进无量纲压力定义[11]，解析求解一维不定常渗流控制方程组，得到动边界运动方程、压力分布和产能公式，进而获得有限导流垂直裂缝井动边界传播规律，指导油田实际生产.

1 数学模型

1.1 物理模型

在河道型均质各向同性储层中心，有一口带有垂直裂缝的生产井，裂缝垂向贯穿储层（见图1），储层厚度为h，裂缝宽度为w，裂缝半长为yf，储层长度为x.当裂缝井以常流量产出微可压缩流体时，忽略重力和毛管力影响，流体流动形式为低速非达西渗流.由于储层狭长、裂缝穿透长度较大，在渗流过程中垂直于裂缝壁面方向上的线性流动占主导地位，可采用双线性复合流动模型进行模拟.

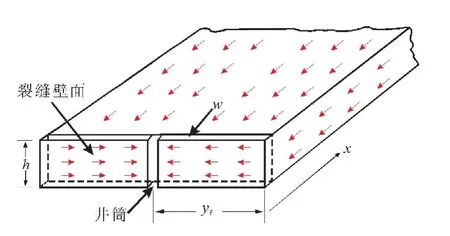
图1 垂直裂缝井剖面Fig.1 Corss-section of a vertical fractured well

1.2 初始条件

对于定井底流量和定流压生产，分别定义无量纲井底压力pD为

式中：K为储层渗透率；q为井产量；μ为流体黏度；B为流体体积系数；p为地层压力；pi为原始地层压力；pwf为井底流压；φ为储层孔隙度；ct为流体压缩系数；xm为压力扰动外边界；λ为启动压力梯度；xD为无量纲x方向距离，xD=x/yf；λD为无量纲启动压力梯度.

定义无量纲时间tD、无量纲动边界位置xmD、无量纲裂缝宽度wfD和无量纲裂缝导流能力cfD为

式中，t为延续生产时间；wf为裂缝宽度.

1.2.1 地层低速非达西渗流

设井位于矩形中心，且井点处为坐标原点，考虑对称性，地层线性流动控制方程为

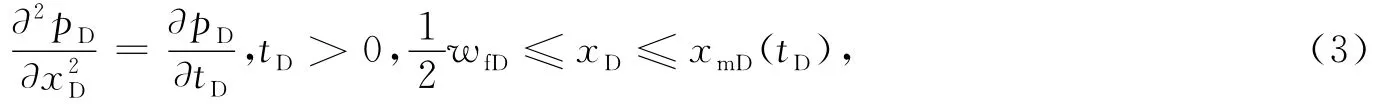
初始条件为

式中：yD为无量纲y方向距离.

动边界条件为

内边界条件为

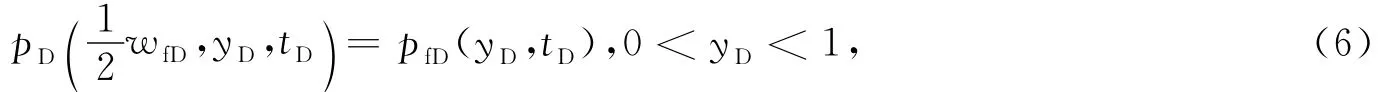
式中：pfD为无量纲裂缝井底压力.式（1）-（6）构成带有动边界的地层一维渗流控制方程组.

1.2.2 裂缝线性流动

裂缝线性流动控制方程为

对于定井底流量和流压生产，内边界方程分别为

裂缝中的流量分布qfD为

式（7）-（9）构成裂缝渗流的控制方程组，它需要与地层渗流方程组耦合求解.

2 模型求解

首先，通过Laplace变换求解地层流体流动模型，得到地层流体的压力分布为

地层条件下的压力传播的动边界方程为

式（8）两边对xD求偏导，得：

然后，对式（7）-（9）做Laplace变换，并将式（12）代入式（7），得到拉氏空间的控制方程组：

井底定流量和定流压时的内边界条件为

将式（14）带入式（13），得到：

（1）井底定流量生产时的井底压力及动边界方程为

（2）井底定流压生产时的地层压力、井底产量及动边界方程为

3 动态特征影响因素

分析井底压力动态特征和井产量递减特征时需求解动边界方程.因为储层存在裂缝，计算时需考虑裂缝导流能力对井底压力及井产量的影响.

设一口有限导流垂直裂缝井，模拟基本参数：B=1.0 m3/m3；μ=1.0 mPa·s；K=3.0×10-3μm2；h=10.0 m；w=5.0 m；φ=0.2；cf=0.005 MPa-1.当无量纲启动压力梯度λD=5，无量纲裂缝导流能力cfD=200时，由式（19）可得在井底定压生产条件下，裂缝不同位置处动外边界随时间的传播规律（见图2）.

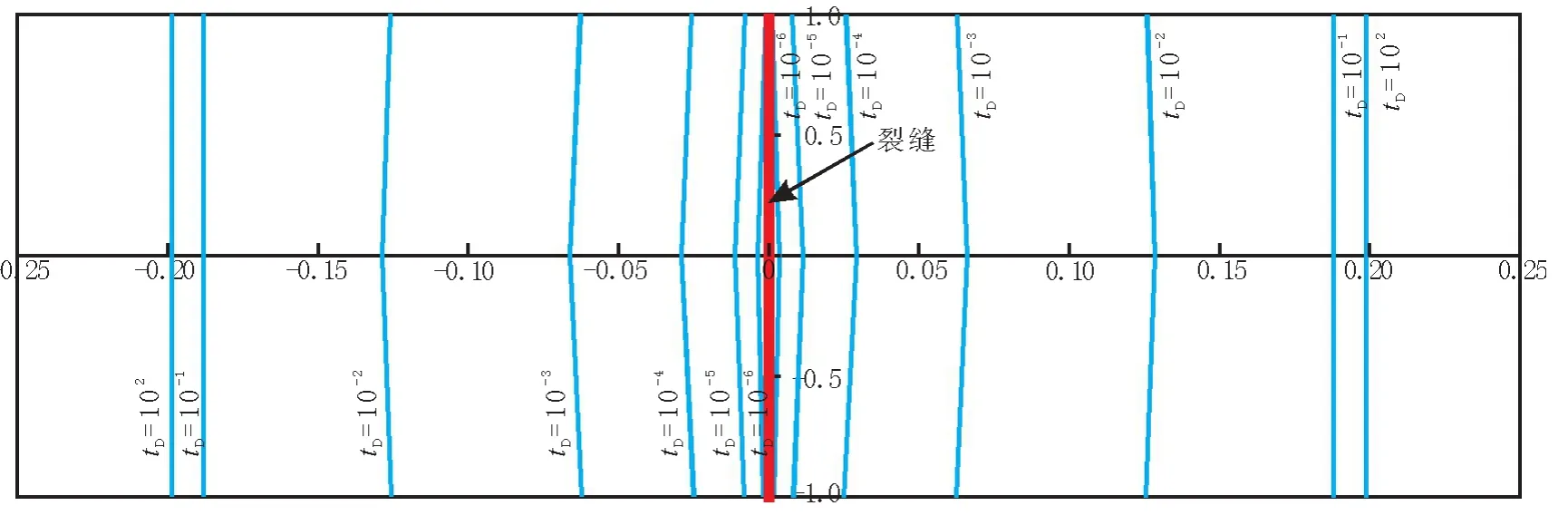
图2 定压条件下动边界传播规律Fig.2 The propagation of moving boundary in the condition of constant pressure

由图2可见，当无量纲时间tD分别为10-6、10-5、10-4、10-3、10-2、10-1和102时，在定井底流压生产情况下，在生产初期，裂缝中点和边缘处的动边界传播速度不同，裂缝中点处动边界传播速度最快，边缘处相对较慢；随着时间的延续，动边界不断扩展，整体呈坡锥的曲线形状，直到达到最大动边界面后停止传播.

3.1 定产条件

3.1.1 无量纲启动压力梯度和裂缝导流能力对动边界的影响

固定井底产量条件下，无量纲启动压力梯度和裂缝导流能力对动边界传播的影响见图3.由图3（a）可见，当无量纲导流能力cfD为10π、无量纲启动压力梯度λD分别为0.100、1.000和5.000时，无量纲动边界xmD在双对数坐标下呈良好的线性关系，且无量纲启动压力梯度λD越大，相同时刻动边界传播距离越短，传播速度越慢；由图3（b）可见，当无量纲启动压力梯度λD为0.010、无量纲裂缝导流能力cfD分别为π、10π和50π时，无量纲裂缝导流能力仅在生产初始阶段对动边界的传播有较小影响，随着时间延长，影响很快消失，且影响很小可被忽略，因此，裂缝可被视为均匀流量裂缝.

图3 固定产量条件下无量纲启动压力和裂缝导流能力对动边界的影响Fig.3 The effect of TPG and fracture conductivity to the dimensionless moving boundary propagation under the condition of constant production

3.1.2 无量纲启动压力梯度和无量纲裂缝导流能力对井底压力/压力导数的影响

固定井底产量条件下，无量纲启动压力梯度和无量纲裂缝导流能力对井底压力/压力导数的影响见图4.图4井底压力/压力导数与时间双对数曲线中，实线为压力时间关系，虚线为压力导数时间关系.图中可见，同一时刻下，当无量纲导流能力cfD为10π时，无量纲启动压力梯度λD越大，无量纲压力pD越大，表明无量纲启动压力梯度引起附加压力损失（见图4（a））.当无量纲启动压力梯度λD为0.010时，早期反映斜率为1/4的裂缝与地层间的双线性流特征；随着流体流动时间延长，曲线反映斜率为1/2的地层线性流特征；无量纲裂缝导流能力cfD越大，无因次压力/压力导数越小，表明早期压力消耗越小，压力变化缓慢（见图4（b））.

图4 固定产条件下无量纲启动压力梯度和裂缝导流能力对井底压力/压力导数的影响Fig.4 The effect of TPG and fracture conductivity to the dimensionless pressure/pressure derivative under the condition of constant production

3.2 定压条件

3.2.1 无量纲启动压力梯度对无量纲动边界的影响

当无量纲裂缝导流能力cfD为30时，定压条件下无量纲启动压力梯度对动边界的影响见图5.由图5可见，当无量纲启动压力梯度分别为0.100、1.000和5.000时，随着无量纲启动压力的增大，无量纲动边界传播距离减小.此外，随着生产时间的延长，无量纲动边界传播距离逐渐增大，压力扰动范围增大，传播速度减慢.时间很大时，对式（19）化简近似可得：当无量纲动边界与无量纲启动压力梯度满足xmD=1.0/λD时动边界停止传播，单井最大动用面积为A=yf（pi-pwf）/λ.

3.2.2 无量纲启动压力梯度对产能的影响

当无量纲裂缝导流能力cfD为30时，定压条件下无量纲启动压力梯度对产量的影响见图6.由图6可见，井产量随生产时间延长而下降.当无量纲启动压力梯度分别为0、0.001、0.100、1.000和5.000时，在生产初期，产量下降幅度较小，双对数曲线反映斜率为-1/2特征；随着生产时间延长，相同时刻无量纲启动压力梯度越大，产量下降幅度越大.

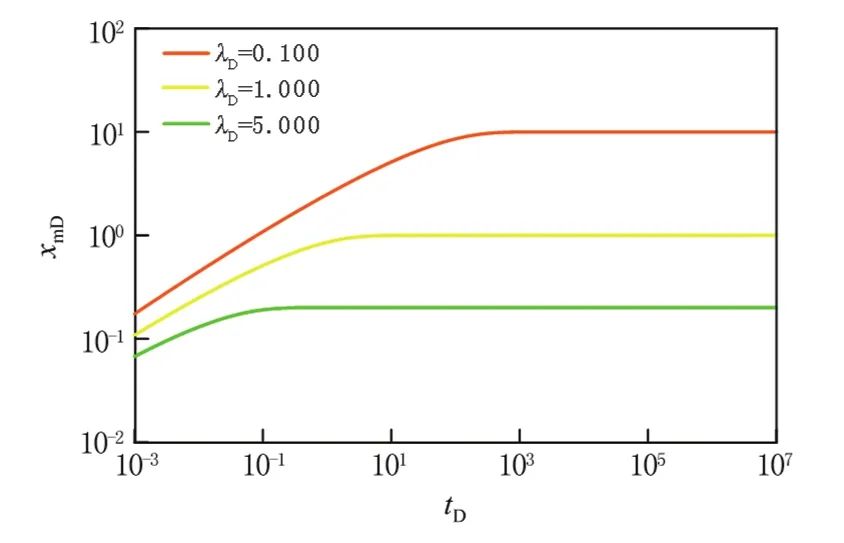
图5 定压条件下无量纲启动压力梯度对无量纲动边界的影响Fig.5 The effect of TPG to the moving boundary under

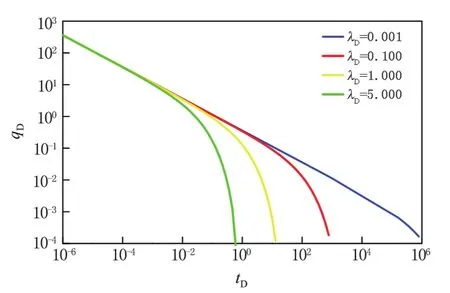
图6 定压条件下无量纲启动压力梯度对井产量的影响Fig.6 The effect of TPG to the well production under the condition of constant pressure the condition of constant pressure

3.2.3 不同时间和启动压力梯度下的井底压力剖面

将式（17）量纲化，分别得到低渗透地层垂直裂缝井定井底流压条件下，当裂缝导流能力为4.5×10-3μm2·m时，不同时间和启动压力梯度的压力剖面（见图7），图7（a）中实线表示启动压力梯度λ为0.020 0 MPa/m，虚线表示启动压力梯度为0 MPa/m.由图7可见，随着生产时间的增加，压力波及范围不断扩大；低渗透地层中流体受启动压力梯度影响，其压力曲线与未受启动压力梯度影响的地层流体压力曲线相交，且启动压力梯度阻碍压力传播（见图7（a））；启动压力梯度越大，压力传播速度越慢，压力波及距离越小，压降漏斗越陡（见图7（b））.

图7 定压条件下不同时间和启动压力梯度时的压力剖面Fig.7 The pressure cross-section of different time and TPG under the condition of constant pressure

4 实例分析

以文中推导的考虑启动压力梯度和裂缝导流能力的双线性渗流时间—压力关系解析方程（见式15）为基础，绘制有限导流垂直裂缝井双对数曲线，以曲线作为解释图版，利用实际测试资料拟合方法，获得垂直裂缝井所在特低、低渗透储层的渗透率、裂缝导流能力、裂缝半长及启动压力梯度等参数.

以现场实际生产井A井为例，对A井的特低渗透层F110层进行压裂后压力恢复测试，根据测试资料绘制的压力恢复双对数曲线具有明显的裂缝特征（见图8）.

利用基于文中推导绘制曲线图版，结合该井和油藏的基本参数对现场实测压力恢复曲线进行解释，得到A井生产储层参数：渗透率为3.086×10-3μm2，裂缝导流能力为1.538μm2·m，裂缝半长为210 m，启动压力梯度为0.020 3 MPa/m.由图8可见，曲线拟合效果良好，该井取得较好压裂效果.

图8 A井双对数拟合曲线Fig.8 Double logarithmic curves of well A

5 结论

（1）利用双线性流模型建立考虑启动压力梯度影响的低渗透无限大油藏渗流模型，分别得到井底定产量及定流压条件下不同启动压力梯度、导流能力的动边界传播规律，以及井底压力、储层压力分布剖面和井底产量图.

（2）对于动边界传播，启动压力梯度越大，动边界传播越慢.对于固定井底产量条件，裂缝导流能力仅在初始阶段对动边界的传播有较小影响，裂缝导流能力越大，压力损耗越小；随着时间的延长，裂缝导流能力对动边界传播的影响小，可忽略不计，裂缝在计算时可视为均匀流量裂缝.

（3）对于固定井底流压条件，动边界随着时间的延长向外传播，裂缝中点处动边界传播速度最快，两边逐渐递减，整体呈坡锥型曲线，达到最大动外边界后停止传播；当最大无量纲动边界满足xmD=1.0/λD时，单井最大动用面积为yf（pi-pwf）/λ；启动压力梯度越大，压降漏斗越陡，产量递减速度越快.

（4）双线性流模型较好地反映流体在低渗储层垂直裂缝井地层及裂缝中的流动，利用典型曲线拟合方法对现场实测资料进行拟合并解释，获得储层渗透率、裂缝导流能力和裂缝半长等动态参数，文中方程与实际有限导流垂直裂缝井情况较为符合.

[1] 尹洪军，刘宇，付春权.低渗透油藏压裂井产能分析[J].新疆石油地质，2005，26（3）：285-287.

Yin Hongjun，Liu Yu，Fu Chunquan.Productivity analysis of fractured well in low permeability reservoir[J].Xinjiang Petroleum Geology，2005，26（3）：285-287.

[2] Prats M.Effect of vertical fracture on reservoir behavior-incompressible fluid case[C].Denver：The 35th Annual Fall Meeting of SPE，1960.

[3] Prats M，Hazebroek P，Strickler W R.Effect of vertical fracture on reservoir behavior-compressible fluid case[C].Dallas：The 36th Annual Fall Meeting of SPE，1961.

[4] 刘慈群.垂直裂缝地层中的流体渗流[J].石油勘探与开发，1987，14（3）：69-73.

Liu Ciqun.The flow of fluid through porous media with a vertical fracture[J].Petroleum Exploration and Development，1987，14（3）：69-73.

[5] 刘慈群.在双重孔隙介质中有限导流垂直裂缝井的非牛顿流体试井分析方法[J].石油学报，1990，11（4）：61-67.

Liu Ciqun.Transient pressure behavior of a well with a vertical fracture with finite-conductivity in a reservoir with double-porosity[J].Acta Petrolei Sinica，1990，11（4）：61-67.

[6] 刘慈群.具有启动压力梯度的油水两相渗流理论与开发指标计算方法[J].石油勘探与开发，1998，25（6）：36-39.

Liu Ciqun.Theory of oil water flow through porous media and calculation of development indexes with starting pressure gradient included[J].Petroleum Exploration and Development，1998，25（6）：36-39.

[7] 邓英尔，刘慈群.低渗油藏非线性渗流规律数学模型及其应用[J].石油学报，2001，22（4）：72-77.

Deng Yinger，Liu Ciqun.Mathematical model of nonlinear flow law in low permeability porous media and its application[J].Acta Petrolei Sinica，2001，22（4）：72-77.

[8] 邓英尔，刘慈群.垂直裂缝井开发低渗油藏非线性渗流压力分析[J].石油勘探与开发，2003，30（1）：81-83.

Deng Yinger，Liu Ciqun.Analysis of pressure of nonlinear flow through low-permeability reservoir with vertically fractured well producing[J].Petroleum Exploration and Development，2003，30（1）：81-83.

[9] Heber Cinco-Ley.Transient pressure analysis for fractured wells：Mexicano del Petroleo[J].SPE 7490，1978.

[10] Lee Shengtai，John R Brockenbrough.A new approximate analytic solution for finite-conductivity vertical fractures[J].Formation Evaluation，SPE 12013，1986.

[11] 王晓冬，侯晓春，郝明强，等.低渗透介质有启动压力梯度的不稳态压力分析[J].石油学报，2011，32（5）：847-851.

Wang Xiaodong，Hou Xiaochun，Hao Mingqiang，et al.Pressure transient analysis in low-permeable media with threshold gradients[J].Acta Petrolei Sinica，2011，32（5）：847-851.

[12] 郭显赋，梁景伟，周密.低速非达西流垂直裂缝井试井模型[J].油气田地面工程，2010，29（10）：14-17.

Guo Xianbing，Liang Jingwei，Zhou Mi.Low velocity non Darcy flow in vertical fractured well test model[J].Oil Gas Field Surface Engineering，2010，29（10）：14-17.

[13] 严涛.低速非达西流有限导流垂直裂缝模型[J].天然气工业，2005，25（2）：130-132.

Yan Tao.Low velocity non-Darcy flow with finite conductivity vertical fracture model[J].Natural Gas Industry，2005，25（2）：130-132.

[14] 付春权，尹洪军，刘宇，等.低速非达西渗流垂直裂缝井试井分析[J].大庆石油地质与开发，2007，26（5）：53-56.

Fu Chunquan，Yin Hongjun，Liu Yu，et al.Well testing analysis of vertical fracture wells with low-velocity non-Darcy flow[J].Petroleum Geology&Oilfield Development in Daqing，2007，26（5）：53-56.

[15] 刘曰武，刘慈群.考虑井筒存储和表皮效应的有限导流垂直裂缝井的试井分析方法[J].油气井测试，1993，2（2）：2-10.

Liu Yuewu，Liu Ciqun.Well test analysis method for finite conductivity vertical fracture wells with wellbore storage and skin effect[J].Well Testing，1993，2（2）：2-10.

[16] 刘永良，徐艳梅，刘彬，等.考虑启动压力梯度低渗双重介质油藏垂直裂缝井试井模型[J].油气井测试，2010，19（5）：5-8.

Liu Yongliang，Xu Yanmei，Liu Bin，et al.Dual medium vertically fractured well in low permeability reservoir with threshold pressure gradients[J].Well Testing，2010，19（5）：5-8.

[17] 闰庆来，何秋轩，尉立岗，等，低渗透油层中单相液体渗流特征的实验研究[J].西安石油大学学报：自然科学版，1990，5（2）：1-6.

Yan Qinglai，He Qiuxuan，Wei Ligang，et al.A study of single phase fluid flow characteristics in low permeability reservoir[J].Journal of Xi'an Shiyou University：Natural Science Edition，1990，5（2）：1-6.

[18] 尹洪军，张荣磊，付春权，等.低渗透均质油藏不稳定压力计算[J].特种油气藏，2008，15（5）：50-52.

Yin Hongjun，Zhang Ronglei，Fu Chunquan，et al.Calculation of transient pressure in Low permeability heterogeneous reservoir[J].Special Oil&Gas Reservoirs，2008，15（5）：50-52.

[19] 李凡华，刘慈群.含启动压力梯度的不定常渗流的压力动态分析[J].油气井测试，1997，6（1）：1-4.

Li Fanhua，Liu Ciqun.Analysis of the pressure dynamic flow of indeterminate with threshold pressure gradient[J].Well Testing，1997，6（1）：1-4.

[20] 程时清，张盛宗，黄延章，等.低速非达西渗流动边界问题的积分解[J].力学与实践，2002，24（3）：15-17.

Cheng Shiqing，Zhang Shengzong，Huang Yanzhang，et al.Integrable decomposition of low velocity non-Darcy flow boundary problem[J].Mechanics in Engineering，2002，24（3）：15-17.

[21] Azari M，Wooden W O，Coble L E.Further investigation on the analytic solutions for finite-conductivity vertical fractures[J].SPE 21402，1991.

[22] Azari M，Wooden W O，Coble L E.A complete set of Laplace transforms for finite-conductivity vertical fractures under bilinear and trilinear flows[J].SPE 20556，1990.

TE348

A

2095-4107（2014）04-0072-08

DOI 10.3969/j.issn.2095-4107.2014.04.011

2014-01-06；

张兆虹

国家科技重大专项（2011ZX05013-004，2011ZX05009-002）

王家航（1988-），男，硕士研究生，主要从事油气田开发方面的研究.