一种基于混合误差梯度下降算法的过程神经网络训练

许少华，宋美玲，许 辰，朱新宁

（东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318）

一种基于混合误差梯度下降算法的过程神经网络训练

许少华，宋美玲，许 辰，朱新宁

（东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318）

针对过程神经网络（PNN）单一训练算法自适应调整能力差、缺乏对学习性质有效控制的问题，提出一种梯度下降与牛顿迭代相结合的求解算法——混合误差梯度下降算法.在训练初始阶段，基于网络训练目标函数，采用梯度下降法进行迭代寻优，只需计算目标函数一阶导数数值公式，复杂度低且误差下降快；当梯度下降法学习效率降低时，引入牛顿迭代法，并将梯度下降法的训练结果作为初始参数代入目标函数，使问题转化为求解非线性方程组，不需要一维搜索而提高网络训练效率.通过学习效率分析自适应调节两种算法的切换，直至满足停机条件.将其应用于时变信号模式分类，实验结果表明，该算法较大地提高PNN训练效率.

过程神经元网络；算法效率；牛顿迭代法；梯度下降法；混合误差梯度下降算法

0 引言

针对时空维信息系统的建模和动态信号处理问题，何新贵院士提出和建立过程神经元网络（Process Neural Networks，简称PNN）理论和模型，证明PNN对L2非线性时变函数的可逼近性、模型的连续性，以及对连续时空维系统建模的可计算性等性质[1-2]，为PNN的应用提供理论基础.与传统神经网络比较，PNN的结构和信息处理机制有很大不同，网络输入和连接权等可以为时变函数，其函数形式和所含参数的位置也具有任意性[3-4]，计算复杂度高，因此，恰当的学习算法设计对于提高PNN建模效率和应用泛化能力具有重要影响.

目前，PNN训练采用的方法主要是基于函数基展开结合最小均方误差准则的学习方法[5-6]，以及与进化算法相结合的优化算法[7-8].Zhong S S等提出基于小波变换的PNN学习算法[9]；Li Ge建立基于混合遗传算法的训练方法[10]；丁刚分别开发PNN基于Legendre正交多项式函数展开和Levenberg-Marquardt训练算法[11]；刘坤等建立一种基于PSO优化的PNN建模方法[12]；李欣等提出PNN量子免疫学习算法[13-15]等.这些研究结果丰富PNN的训练方法，提高网络模型的应用能力，但是单一算法的计算复杂度与输入信号的复杂性、网络规模呈倍数增加，待定参数冗余且自由度大；同时，在训练过程中算法的自适应调整能力差，缺乏对学习性质的有效控制，在应用中对训练样本集的构建也有较高的要求，系统的建模效率也较低.

笔者提出一种基于梯度下降—牛顿迭代相结合的过程神经网络混合误差梯度下降学习方法.梯度下降法只需计算目标函数一阶导数，利用等价的数值迭代公式求解时计算复杂性小、误差下降速度快，针对训练目标函数，在网络学习的初始阶段使用梯度下降法[16].当梯度下降法学习效率降低时，基于网络训练目标函数引入牛顿迭代法[17]，并将梯度下降法当前的训练结果作为初始参数代入目标函数，使问题转化为求解非线性方程组.设置基于学习效率分析的切换条件，两种算法自适应交替使用，在机制上可有效提高PNN的训练效率.

1 权函数基展开PNN模型

考虑一种网络权函数被一组已知函数基展开的过程神经网络模型，它与PNN基本模型[13]具有等价的信息处理机制，是在满足拟合精度要求的前提下，将权函数表示为基函数的有限项展开形式.在应用中，只需要根据非线性时变系统的概率统计性质选择适当的函数基，即可采用传统神经网络已有的成熟学习算法进行系统建模和网络训练.

设x（t）∈U⊂Rn，其中，t∈[0，T]，U∈C[0，T]n.为不失一般性，只讨论多输入/单输出PNN模型，将其结果容易推广到多输出的情况.假设PNN的权函数可被U中的一组有限函数基B（t）=（b1（t），b2（t），…bL（t））展开，其中L为满足U中函数基展开拟合精度的最小项数，则权函数基展开PNN的结构见图1.

其中，xi（t）为系统输入函数，“∫”和“Σ”分别为过程神经元的时、空聚合算子，f为作用函数.权函数wij（t）用基函数展开的形式表示，中间各子层的运算公式为

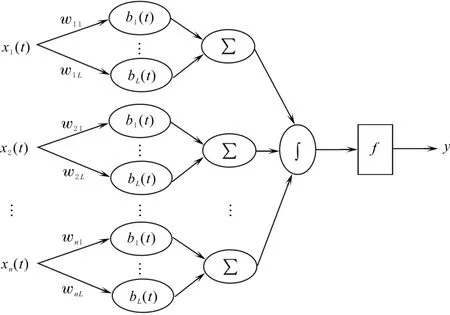
图1 权函数基展开PNN模型Fig.1 Process neural network based on weight function basis expansion

写成一般映射函数形式为

若取K（·）为恒等变换函数，则PNN输入与输出之间的映射关系（见图1）为

根据最小误差准则，网络训练目标函数定义为

式中：yk为对应第k个输入函数样本的网络实际输出.

2 基于梯度下降—牛顿迭代法结合的PNN训练算法

2.1 PNN梯度下降算法

式中：▽E（W（k））为E（W）的一阶梯度；α（k）为迭代效率因子

2.2 PNN牛顿迭代算法

在式（6）中，记

则PNN的求解问题等价于

式（8）为一个非线性方程组，包含K个方程和n Lm+2m个未知参数.当K≤n Lm+2m，且系数矩阵满足严格对角占优条件时，式（8）存在解.采用牛顿迭代法进行求解：

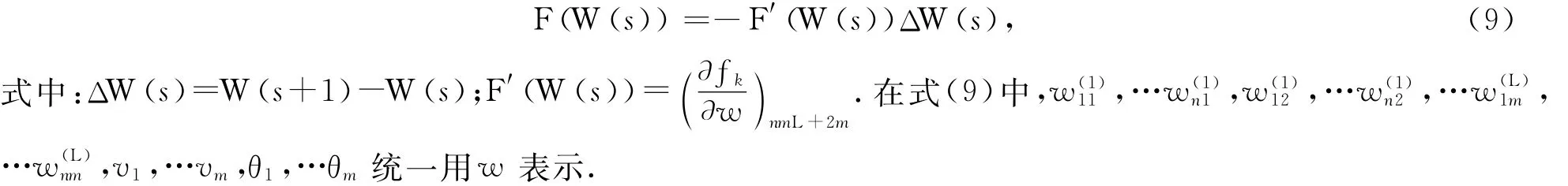
2.3 PNN梯度下降—牛顿迭代训练算法

考虑PNN训练算法的效率，建立梯度下降和牛顿迭代算法的切换准则：设θ为效率阈值，ΔL为设置算法运行的迭代间隔，ΔE为经ΔL次迭代后E的变化量.若，则进行不同算法切换.PNN基于梯度下降—牛顿迭代结合的混合误差梯度下降训练算法描述为

Step 1：设置训练误差精度ε＞0，最大学习步数M、效率阈值θ和迭代间隔次数ΔL.

Step 2：执行梯度下降法，在[0，1]区间初始化网络连接权值W（0）.

Step 3：按式（7）进行ΔL次循环迭代，计算ΔE.

Step 5：若满足终止条件，则保存目前解停机；否则，执行Step 6，切换到牛顿迭代法.

Step 6：执行牛顿法，W 设置为上一阶段算法计算的结果；按式（9）进行ΔL次循环迭代，计算ΔE.

Step 8：若满足终止条件，保存目前解并停机.

3 实验分析

采用具有不规则函数信号发生器加噪声产生3类、60个分段指数型时变波形信号，函数的幂指数和分段区间在一定范围内随机设定.其中，第1类信号幂指数取值区间为[1.0，1.5]，分段区间长度在[0.9，1.0]内随机设定；第2类信号幂指数取值区间为[1.9，2.2]，分段区间长度在[0.8，1.1]内随机设定；第3类信号参数取值区间分别为[2.9，3.3]和[0.7，1.2].经归一化处理后，构成统一的过程信号采样区间[0，1].

利用PNN（见图1）对时变信号进行模式分类.对60个信号样本在误差精度0.05下进行基于Walsh函数基的展开，当基函数项数为32时，达到拟合精度要求.PNN的结构确定为：1-32-1，即1个连续信号输入节点、32个Walsh函数基节点、1个时空聚合过程神经元输出节点.随机用40个信号函数构成学习样本集，20个信号样本组成测试集，训练误差精度设为0.05.分别用基于正交基展开算法[3]、Fourier函数变换算法[15]和基于梯度下降—牛顿迭代结合算法（ΔL=30，θ=0.05）对网络进行训练，总的迭代次数均设定为3 000，每种算法运行10次，训练结果见表1.

表1 3种算法PNN训练结果Table 1 The results of three train algorithms for PNN

由表1可见，在梯度下降—牛顿迭代结合算法中，梯度下降法和牛顿迭代法的平均切换次数为4.6次.梯度下降—牛顿迭代结合算法，与PNN函数正交基展开算法训练算法和Fourier函数变换算法相比，正确识别率基本相同，但学习效率有较大提高.这是由于在整个训练过程中实现两种算法的自适应切换，当一种算法略显停滞时立即切换到另一算法，因而有效实现两种算法的优势互补.

4 结束语

提出一种基于梯度下降与牛顿迭代相结合的过程神经网络训练算法.该算法将PNN训练的泛函寻优转换为对多元函数求极值的优化问题，综合利用两种方法不同的求解特性，通过基于效率分析的自适应切换策略，实现网络参数在可行解空间的全局求解.该算法具有明显优于单一算法的收敛速度和逼近能力，对于其他机器模型的学习和复杂函数的优化等问题的解决具有一定的参考和借鉴价值.

[1] 何新贵，梁久祯.过程神经元网络的若干理论问题[J].中国工程科学，2000，2（12）：40-44.

He Xingui，Liang Jiuzhen.Some theoretical issues on process neural networks[J].Engineering Science，2000，2（12）：40-44.

[2] 许少华，何新贵.关于连续过程神经元网络的一些理论问题[J].电子学报，2006，34（10）：1838-1842.

Xu Shaohua，He Xingui.Some theoretical issues on continuous process neural networks[J].Acta Electronica Sinica，2006，34（10）：1838-1841.

[3] 刘显德，刘立伟，许少华.一种过程神经元网络模型及其在动态预测中的应用[J].大庆石油学院学报，2008，32（4）：107-110.

Liu Xiande，Liu Liwei，Xu Shaohua.A process neural networks model and its application to dynamic forecasting[J].Journal of Daqing Petroleum Institute，2008，32（4）：107-110.

[4] 许少华，王皓，王颖.基于过程神经网络的多维动态信息处理技术[J].大庆石油学院学报，2010，34（5）：145-164.

Xu Shaohua，Wang Hao，Wang Ying.Multidimensional dynamic information processing based on process neural networks[J].Journal of Daqing Petroleum Institute，2010，34（5）：145-164.

[5] 许少华，何新贵.基于函数正交基展开的过程神经元网络学习算法[J].计算机学报，2004，7（5）：645～650.

Xu Shaohua，He Xingui.Learning algorithms of process neural networks based on orthogonal function basis expansion[J].Chinese J of Computers，2004，27（5）：645-649.

[6] 许少华，肖红.基于离散Walsh变换的过程神经元网络学习算法[J].大庆石油学院学报，2003，27（4）：58-61.

Xu Shaohua，Xiao Hong.Learning algorithm of process neural networks based on discrete Walsh conversion[J].Journal of Daqing Petroleum Institute，2003，27（4）：58-61.

[7] Kaveh A，Talatahari S.Particle swarm optimizer，ant colony strategy and harmony search scheme hybridized for optimization of truss structures[J].Computers&Structures，2009，87（5）：267-283.

[8] Ababu Teklemariam Tiruneh.Higher order aitken extrapolation with application to converging and diverging Gauss-Seidel iterations[J].Journal of Applied Mathematics and Physics，2013，1（5）：128-143.

[9] Zhong S S，Li Y，Ding G.Continuous wavelet process neural network and its application[J].Neural Network World，2007，17（5）：483-495.

[10] Li Ge，Yin Guisheng.Application of double hidden layer process neural network on wood drying modeling[C]∥Proceedings of 2011 IEEE the 18th International Conference on Industrial Engineering and Engineering Management（Volume 3）.Bejing：Electronic Industry Press，2011.

[11] 丁刚.过程神经网络泛化能力的理论与应用研究[D].哈尔滨：哈尔滨工业大学，2008.

Ding Gang.Generalization capability of process neural network and its applications[D].Harbin：Harbin Institute of Technology，2008.

[12] 刘坤，谭营，何新贵.基于粒子群优化的过程神经网络学习算法[J].北京大学学报，2011，47（2）：238-244.

Liu Kun，Tan Ying，He Xingui.Particle swarm optimization based learning algorithm for process neural networks[J].Acta Scientiarum Naturalium Universitatis Pekinensis，2011，47（2）：238-244.

[13] 荆献勇，肖明清，余文波.改进免疫算法在预测过程神经网络中的应用[J].系统工程与电子技术，2010，32（10）：2136-2140.

Jing Xianyong，Xiao Mingqing，Yu Wenbo.Application of improved immune algorithm in forecast procedure neural network[J].Systems Engineering and Electronics，2010，32（10）：2136-2140.

[14] 葛利.一种基于混合遗传算法学习的过程神经网络[J].哈尔滨工业大学学报，2005，37（7）：986-988.

Ge Li.Procedure neural networks based on being learned by hybrid genetic algorithm[J].Journal of Harbin Institute of Technology，2005，37（7）：986-988.

[15] 李欣，程春田.基于过程神经网络和量子免疫算法的油气评价[J].计算机工程与应用，2008，45（25）：9-13.

Li Xin，Cheng Chuntian.Evaluation method of oil and gas resource based on process neural network and quantum immune algorithm[J].Computer Engineering and Applications，2008，45（25）：9-13.

[16] 关治，陆金普.数值分析基础[M].北京：高等教育出版社，1998.

Guan Zhi，Lu Jinpu.Numerical analysis[M].Beijing：China Higher Education Press，1998.

[17] 王能超.同步并行算法设计[M].北京：科学出版社，1996.

Wang Nengchao.Design of synchronous parallel algorithm[M].Beijing：Science Press，1996.

TP183

A

2095-4107（2014）04-0092-05

DOI 10.3969/j.issn.2095-4107.2014.04.014

2014-03-31；

任志平

国家自然科学基金项目（61170132）

许少华（1962-），博士后，教授，博士生导师，主要从事人工神经网络、优化算法和可视化数据建模方面的研究.