40Cr调质钢高速冷滚打热力耦合数值模拟

张丰收，姚海波，崔凤奎，朱文娟

（河南科技大学1.医学技术与工程学院；2.机电工程学院 ，洛阳 471003）

0 引 言

高速冷滚打成形技术是利用金属材料在常温下的固有塑性，通过一定形状的滚打轮对工件进行断续击打，使其渐变塑性成形，从而形成零件廓形的一种绿色、净近塑性成形技术［1］。在高速冷滚打成形过程中，工件在发生变形的同时温度也在发生变化，分布不均的温度对材料变形抗力的影响很大，进一步影响工件的流动特性，因此研究高速冷滚打成形过程中的热力耦合作用形成机制对于揭示塑性成形过程中的金属流动规律具有一定的理论意义。

目前，已有一些学者采用理论解析、试验研究和数值模拟的方法，分析了高速冷滚打成形的形成机理［2］，并对滚打轮的设计［3］、弹塑性修正［4－5］和冷滚打零件组织［6－7］进行了研究。但多数研究都是基于纯力学和材料学进行的，没有涉及冷滚打过程中产生的热效应，而热效应引起的工件内部不均匀的温度场将影响工件金属的流动性，进而对成形零件质量和性能产生影响［8－9］。

因此，作者在分析高速冷滚打成形原理的基础上，对高速冷滚打成形过程中热力耦合作用形成过程进行了研究，建立了温度场的数学模型，推导了模型的求解过程。基于ABAQUS/Explicit平台建立了40Cr调质钢高速冷滚打成形三维有限元模型，分析了该材料高速冷滚打过程的热力耦合形成机制及滚打轮转速对工件温度场分布的影响，最后进行了试验验证。

1 冷滚打热力耦合作用的形成过程

根据高速冷滚打成形原理［2］，滚打轮在击打工件的过程中，它们之间的相对运动为纯滚动。滚打过程中滚打轮与工件瞬间高速碰撞，力的瞬态作用使能量耗散在局部区域，使工件材料瞬间形成剧烈的大应变，高应变速率和大应变的形成并非是一个纯力学过程，而是包含了能量转化以及温度、显微组织改变交互作用的过程。由于在滚打过程中，工件局部会发生剧烈的塑性变形，从而使得局部温度的改变比较明显，温度场通过与温度相关的材料物理机制的变化来影响显微组织场，进而影响变形场。与此同时，变形场又通过能量耗散和热传导来影响温度场，这是典型的热、力耦合效应。具体表现在以下四个方面：（1）滚打轮的旋转动能使工件发生塑性变形，导致工件内部能量耗散，滚打轮与工件之间的摩擦行为对工件变形温度场产生影响；（2）工件材料变形温度场通过与温度相关的工件材料本构方程对工件的变形场（应力场、应变场）产生影响；（3）滚打轮与工件之间的运动接触热边界（滚打轮与工件之间的热传导、滚打轮和工件与环境的热辐射、热对流）对工件变形场和温度场产生影响；（4）工件材料的物性参数、热膨胀产生的温度历史效应对工件的应力场和应变场产生影响。

2 温度场数学模型的建立

高速冷滚打成形过程中能量的转化应满足能量守恒定律，即热力学第一定律：

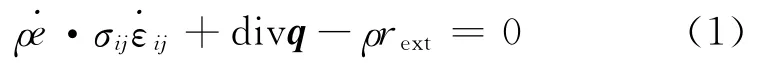
式中：ρ为材料的密度；e为单位质量的内能；σij为Cauchy应力张量分量；εij为应变张量分量；rext为外

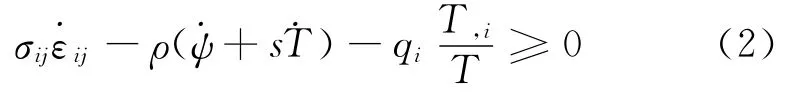
式中：ψ为Helmholtz自由能；s为比熵；T为热力学温度；T，i为温度梯度，即温度在坐标轴i方向上的导数。

由勒让德变换定义的热力学状态函数Helmholtz自由能为

Helmholtz自由能的内部状态变量形式为

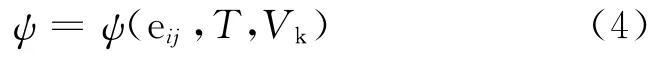
式中：Vk为内变量；εeij为弹性应变张量分量，εeij＝εij－εpij；εpij为塑性应变张量分量。

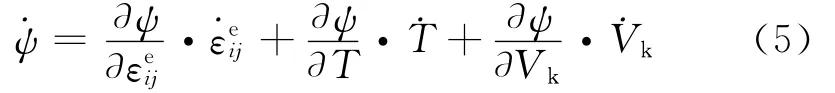
对式（4）进行求导得热的质量密度；q为热流矢量。

高速冷滚打成形过程中不仅要满足能量守恒定律，而且能量的转移需要遵循特定的方向，需要满足热力学第二定律。

将式（5）代入式（2）得

式中：vk为内变量的相对速度分量。

式（6）对任意状态变量的可逆变换是有效的，而冷滚打成形过程是不可逆的，因此式（6）的前两项应为零，由此得到冷滚打热力学状态函数为

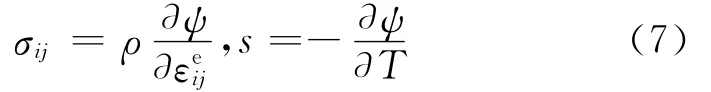
式（6）中剩余部分为冷滚打成形过程中的不可逆耗散能

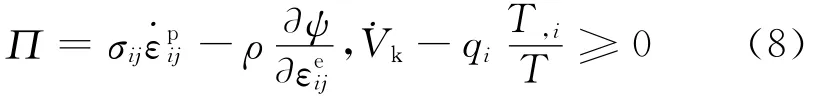
对式（3）进行求导并代入式（1）得

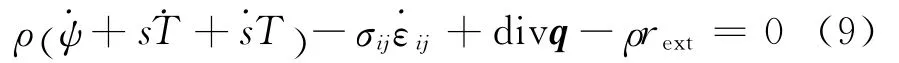
将式（5）代入式（9），并利用式（7）可以得到冷滚打成形过程中工件塑性耗散的热传导能量平衡式：

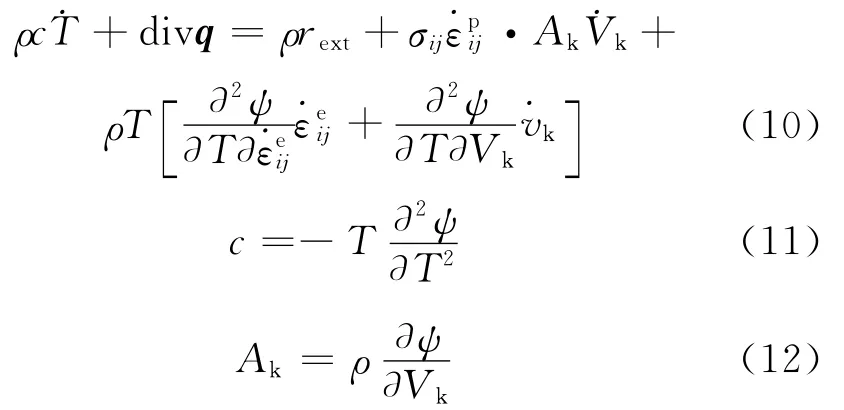
式中：c为热容；Ak为内变量Vk对应的热力学力。

高速冷滚打成形是冷塑性变形，没有外部热源，式（10）中等号右边第一项为零，则式（10）变为

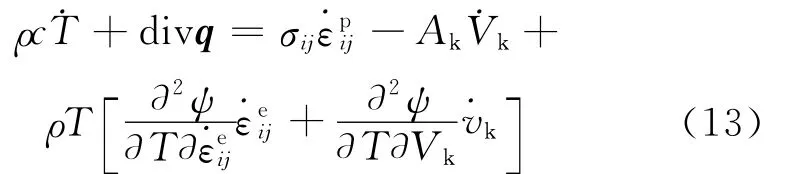
在一定的初始条件和边界条件下，求解式（13）便可获得考虑热力耦合效应的冷滚打成形过程中工件的温度分布及其变化规律。

3 有限元模型的建立

3.1 几何模型的建立

由于高速冷滚打成形过程是两个相同转速的滚打轮逆向旋转对工件进行击打成形，是一个轴对称过程，故模拟分析时考虑工件的1/2便可。工件的进给速度较小（1mm·s－1），为节省计算时间又不影响模拟的精度，取长度为12mm的圆柱体工件，几何模型如图1所示，工件网格划分如图2所示。圆柱体工件半径为20mm，滚打轮半径、轮齿宽度及圆角半径分别为19，8，2mm。

图1 滚打轮的几何模型Fig.1 Geometric model of rolling

3.2 初始条件

在高速冷滚打成形过程中，工件温度随时间而变化，形成的工件温度场是瞬态温度场，求解瞬态温度场问题是在初始条件下，满足高速冷滚打能量平衡热传导方程式（13）。初始条件为T＝，为基准平均温度。

3.3 边界条件

高速冷滚打成形过程中，工件的局部大应变瞬

图2 工件网格划分Fig.2 Unit meshing

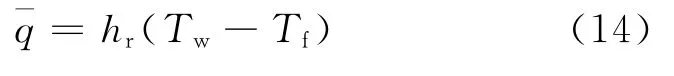
式中：hr为对流换热系数；Tf为工件周围环境温度；Tw为工件表面温度。

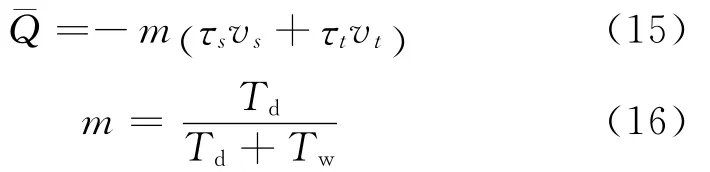
式中：τs和τt分别为接触表面径向和轴向的接触应力分量；vs和vt为相应接触点处的相对速度分量；m为热量分配系数；Td为滚打轮表面温度。

3.4 40Cr调质钢模型的建立

40Cr调质钢因具有高强度和良好的延展性而成为高速冷滚打成形工件的主要材料，在高速冷滚打塑性变形过程中存在着高应变速率和大变形等众多复杂因素，为了分析应变速率、温度和加工硬化对其流变应力的影响，进行了5组动态压缩试验和1组静态压缩试验。在常温下选取3组应变速率（1 072，2 534，5 160s－1）进行动态压缩试验，温度200℃下选取1 193s－1，400℃下选取1 380s－1进行动态压缩试验；在常温下进行应变速率为0.004，632s－1的静态压缩试验。试验结果如图3，4所示，可见，40Cr调质钢具有明显的应变速率和温度敏感性，其流变应力随应变速率的增大和温度的降低而增大。

Johnson-Cook模型是一种经验粘塑性本构方程，能较好地描述材料在高应变速率下的加工硬化效应、应变速率效应和温度效应，并且形式简单，使用5个参数就能较好地描述材料的力学行为，适用于各种晶体结构，在工程中应用较广泛。将该模型用于40Cr调质钢的流动应力描述，Johnson-Cook流变应力表达式为

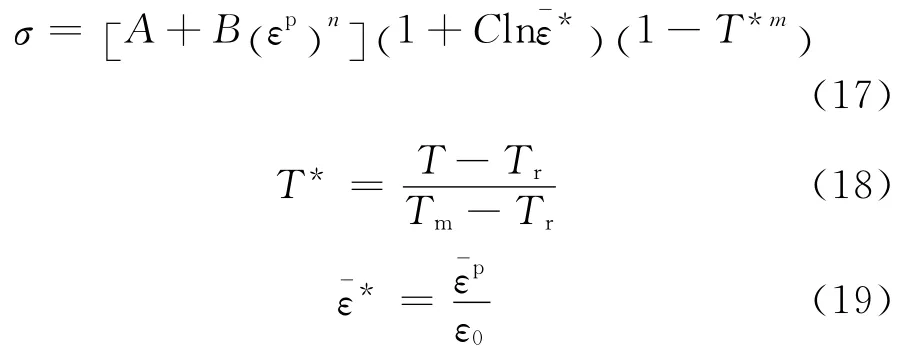
式中：σ为流变应力；C为材料应变速率强化参数；εp为等效塑性应变；A为屈服应力；B为应变硬化系数；n为应变硬化指数；m为温度敏感系数；T，Tm，Tr分别为试验温度、试样的熔点以及参考温度（20℃）；˙ε0，˙εp分别为参考应变速率、等效塑性应变速率，˙ε0＝0.004s－1。

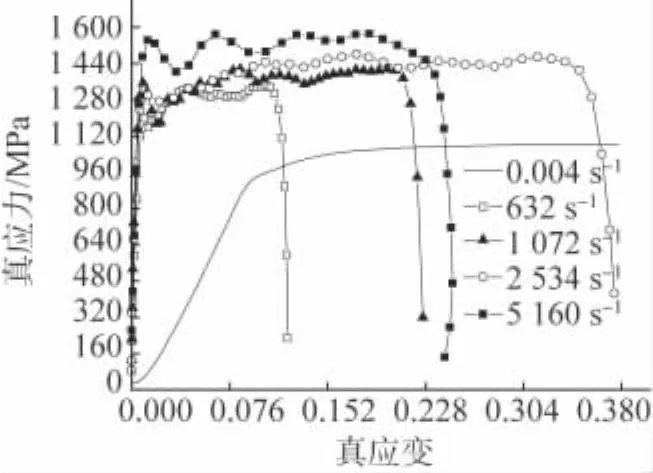
图3 常温及不同应变速率下40Cr调质钢的压缩真应力－真应变曲线Fig.3 True stress and true strain curves of 40Cr quenched and tempered steel compressed at different strain rates at room temperature

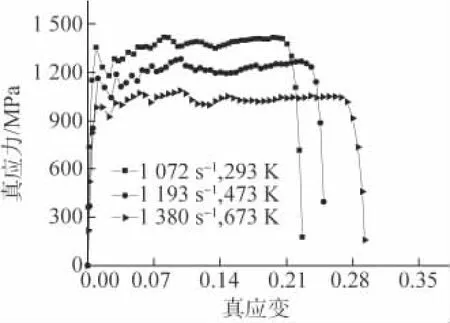
图4 不同应变速率和温度下40Cr调质钢的压缩真应力－真应变曲线Fig.4 True stress and true strain curves of 40Cr quenched and tempered steel compressed at different strain rates and temperatures

通过拟合试验数据求解Johnson-Cook本构方程参数，得到40Cr调质钢的流变应力表达式为

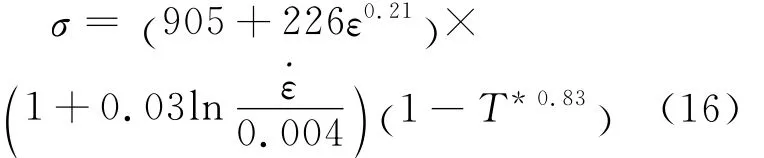
图5是不同温度下Johnson-Cook本构方程预测的流变应力与试验数据的对比，可以看出，在1 072，1 193，1 380s－1下，随着温度从293K 升高至673K，以及应变速率的增大，因热软化效应导致流变应力明显下降，Johnson-Cook模型预测的不同温度下的流变应力与试验数据基本吻合，能较好地描述40Cr调质钢在不同温度下的流变应力。

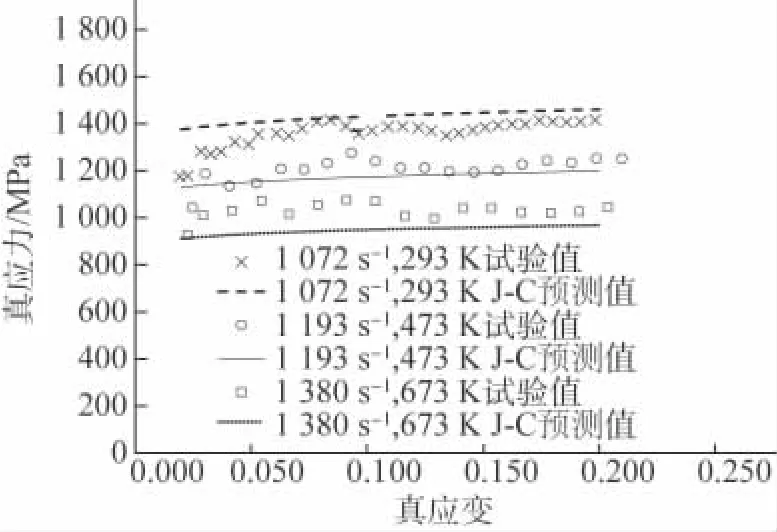
图5 不同温度下40Cr调质钢J-C模型预测的流变应力与试验数据的对比Fig.5 Comparison of flow stress by J-C model prediction and experiment of 40Cr quenched and tempered steel at different temperatures

40Cr调质钢的J-C模型参数如表1所示，物理参数如表2所示［3］。

表1 40Cr调质钢的J-C模型参数Tab.1 J-C model parameters of 40Cr quenched and tempered steel

由于滚打轮击打工件的深度为3mm，是局部接触，故对工件进行分块划分网格，在局部接触部分，网格的单元等分线段长度为0.2mm，其它部分网格的单元等分线段长度为2mm，工件网格划分如图2所示，单元个数为165 960。高速冷滚打热力耦合和不考虑热作用的有限元模拟单元类型分别为C3D8RT和C3D8R。滚打轮为解析刚体，无需划分网格。约束滚打轮有5个方向的自由度，在其刚性参考点上加载转速（2 000r·min－1），在工件的全部节点上加载其进给量（1mm·s－1），在工件的对称面施加轴对称约束，接触类型为面面接触，摩擦形式为剪切摩擦。

3.5 模拟结果与分析

由图6～8可以看出，工件冷滚打变形后两侧突起，中间凹陷，这是由于工件金属的流动符合最小阻力定律和金属体积不可压缩性。冷滚打成形过程中温度场与应变场的分布规律类似，并且工件的应力场、应变场和温度场分布是不均匀的。不均匀的变形区大致可分为剧烈变形区、小变形区和难变形区。在剧烈变形区内，工件的等效塑性应变大，温升高；小变形区内工件的等效塑性应变小，温升低。在高速冷滚打成形过程中，工件的应变场和温度场是同时产生、相互影响且交互作用的，工件的塑性变形功、滚打轮与工件之间的摩擦功转化为热量使工件温度变化的同时，工件材料与温度有关的力学和热物理性能也发生相应的变化，温度场对应变场的影响主要是通过本构方程来实现（本构方程中工件材料的流变应力表示为应变、温度和应变速率的函数），变化的温度场在改变金属流变应力场的同时，也使工件的应变场发生改变。其实质是能量的转化，在高速冷滚打成形过程中，滚打轮的旋转动能对工件输入的能量主要是通过本构方程来实现的，大致表现在两个方面。一是工件的塑性变形，其中大部分转化为使工件产生温度变化的热量，少量存储于工件中；二是工件的弹性变形，冷滚打成形过程中能量转化平衡式为

表2 40Cr调质钢的物理参数Tab.2 Physical parameters of 40Cr quenched and tempered steel

图6 冷滚打不同时刻工件的等效应力分布云图（MPa）Fig.6 Equivalent stress distributions of the workpiece in cold rolling at different times

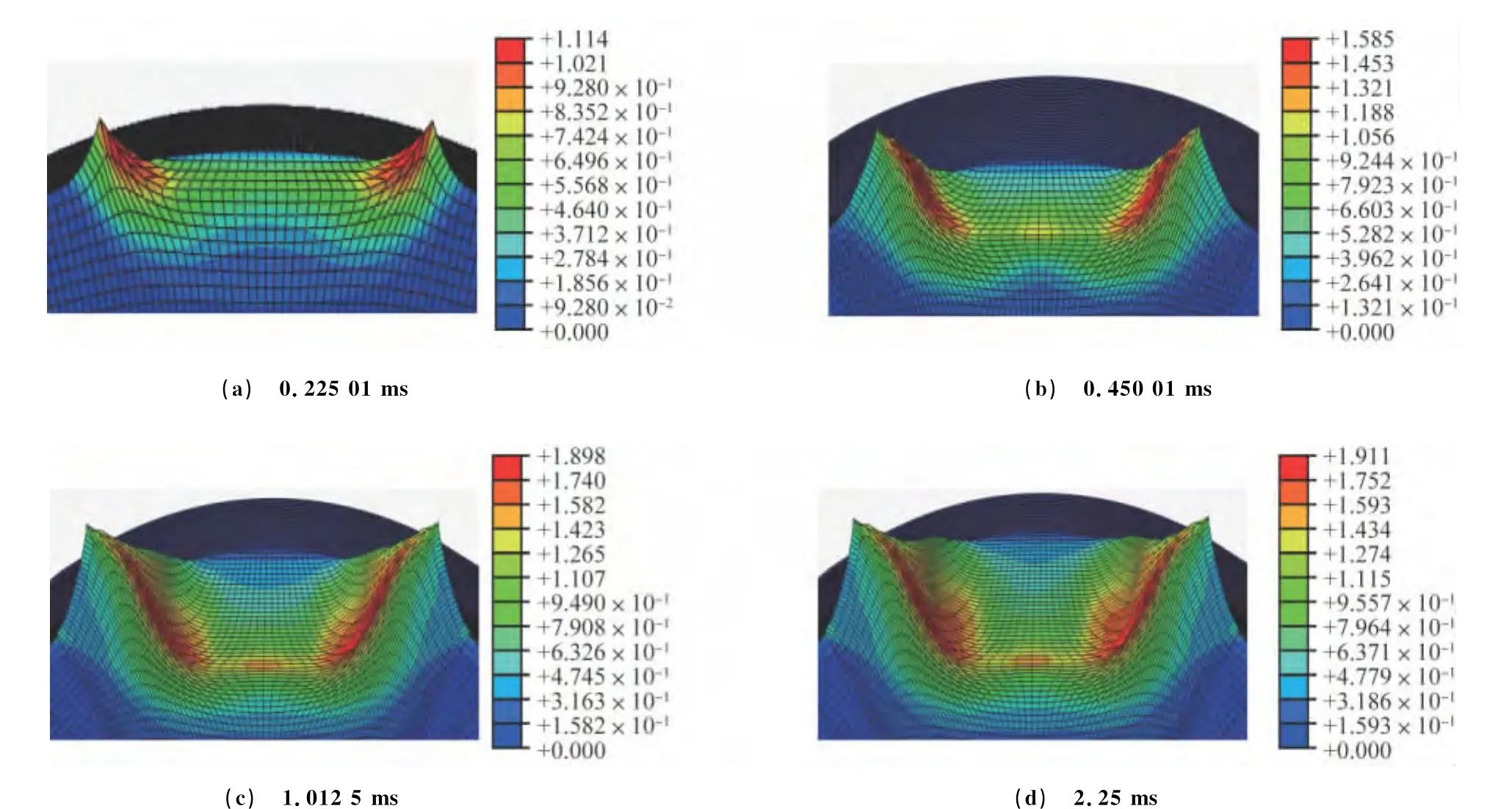
图7 冷滚打不同时刻工件的等效应变分布云图Fig.7 Equivalent strain distributions of the workpiece in cold rolling at different times

图8 冷滚打不同时刻工件的温度场分布云图（K）Fig.8 Distributions of temperature field of the workpiece in cold rolling at different times

Ei＝Eel＋Ep＝Eel＋Es＋Ed（20）式中：Ei为总能量；Eel为弹性变形能；Ep为塑性变形能；Es为存储能；Ed为耗散能。

4 试验验证

为研究冷滚打成形中热力耦合对工件应力应变的影响，搭建自制裂纹柔度法试验平台。

工件采用一根40Cr冷滚打渐开线花键轴 （未经过热处理），利用DK7725FD型线切割机床进行局部切割；采用B×120-0.5AA型传感器、灵敏系数为2.08的应变片，利用PSD-702型静态电阻应变仪测应变。

由图9可见，热力耦合数值模拟的等效应力随应变的增大而减小，不考虑热效应的等效应力数值模拟结果随应变的增大而增大。这是因为，40Cr调质钢具有明显的应变速率和温度敏感性，流变应力随温度的升高而降低。高速冷滚打成形是工件加工硬化和动态软化同时作用的过程，这两个过程都与金属的位错密度密切相关，其实质是滚打轮的旋转动能在金属内部形成较大的内应力，使其晶粒内部产生滑移，引起工件的位错密度发生变化。硬化过程中位错密度增大，软化过程中位错密度减小，加工硬化与动态软化是由位错的聚集与抵消引起的，是两个的相反过程，其综合效果将受到变形温度、变形速率及变形量的影响。随着冷滚打成形过程的进行，流变应力随应变增大而增大，工件产生硬化，同时，工件中的塑性变形功转化成热量引起软化，并且随着应变的增大，软化作用引起的流变应力的下降大于硬化作用引起的上升。

试验结果与考虑热力耦合的摸拟结果基本一致，由于所取单元与测量部位不能完全对应，而且实测时存在热量散失，故试验结果与模拟结果仍存在一定的误差。

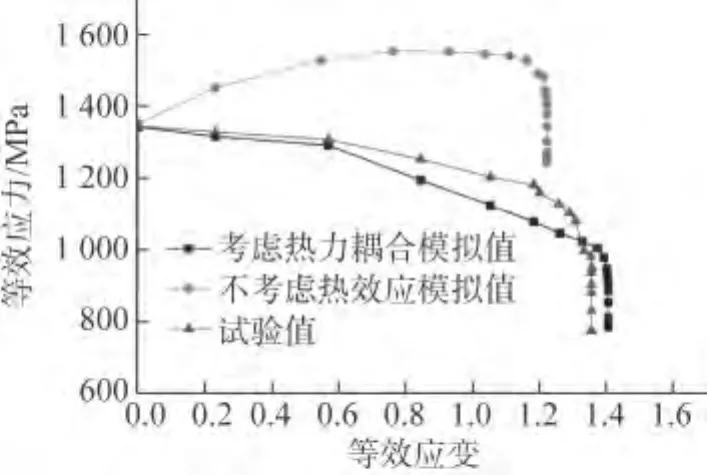
图9 考虑热力耦合及不考虑热效应模拟的等效应力－等效应变曲线及其试验值Fig.9 Equivalent stress and equivalent strain curves from simulation considering thermo-mechanical coupling and without considering thermal effect and from experiment

5 结 论

（1）工件的温度分布和等效塑性应变分布是不均匀的，剧烈应变区的等效塑性应变高，温升高，难变形区的等效塑性应变低，温升低。

（2）高速冷滚打成形时，工件初始温度很低，应主要考虑不可逆塑性变形功的热耗散和工件、滚打轮截面摩擦生热效应；试验结果证明了模拟结果的正确性。

［1］崔凤奎，李言，周彦伟，等.渐开线花键轴冷滚轧工艺试验［J］.农业机械学报，2006，37（12）：189-192.

［2］朱国明，康永林，陈伟，等.H型钢空冷过程中残余热应力的有限元分析［J］.机械工程材料，2008，32（4）：77-80.

［3］CUI Feng-kui，WANG Xiao-qiang，ZHANG Fang-shou，et al.Metal flowing of involute spline cold roll-beating forming［J］.Chinese Journal of Mechanical Engineering，2013，26（5）：1056-1062.

［4］张璐，李言，杨明顺，等.丝杠冷滚打成形过程金属流动规律研究［J］.中国机械工程，2012（13）：1623-1628.

［5］张璐，杨明顺，李言，等.高速冷滚打过程变形力解析方法及其修正［J］.塑性工程学报，2011（5）：1-7.

［6］欧新哲，杨合，孙志超，等.环件热辗扩温度场和应变场分布的研究 ［J］.机械工程材料，2006，30（10）：80-87.

［7］崔凤奎，徐永福，赵魏.花键冷滚打和铣削加工的金属组织变形研究［J］.锻压技术，2008，33（2）：70-74.

［8］ABEDRABBO N，POURBOGHRAT F，CA RSLEY J.Forming of AA5182-O and AA5754-O at elevated temperatures using coupled thermo-mechanical finite element models［J］.International Journal of Plasticity，2007，23（5）：841-875.

［9］何涛，王宝雨，胡正寰.Inconel718合金楔横轧成形热力耦合模拟［J］.塑性工程学报，2008，15（3）：157-159.