悬臂梁振型的弯曲变形和剪切变形分解①

陈光远

(同济大学土木工程学院，上海 20092)

0 引言

经典的梁理论分为 Euler－Bernoulli梁和Timoshenko梁.Euler－Bernoulli梁只适用于细长梁，且只有在梁的低频振动时才和理论结果相近.由于忽略了梁的剪切变形，致使梁的刚度被高估，自振频率高于理论值.Timoshenko在1921年提出了Timoshenko梁理论，这个理论同时考虑了梁的弯曲变形引起的转动惯量和梁的剪切变形，大大改善了以往梁的动力学理论.Timoshenko梁理论指出，梁的长细比越小，振型阶数越高，剪切变形的影响越大.在Timoshenko之后，又有很多学者对梁的横向振动问题进行了更深入的研究[1～5].对高层建筑结构的研究可以简化为一根悬臂梁进行定性研究，本文将从悬臂梁各阶振型的剪切变形分量、弯曲变形分量以及剪切应变能和弯曲应变能的角度进行研究.

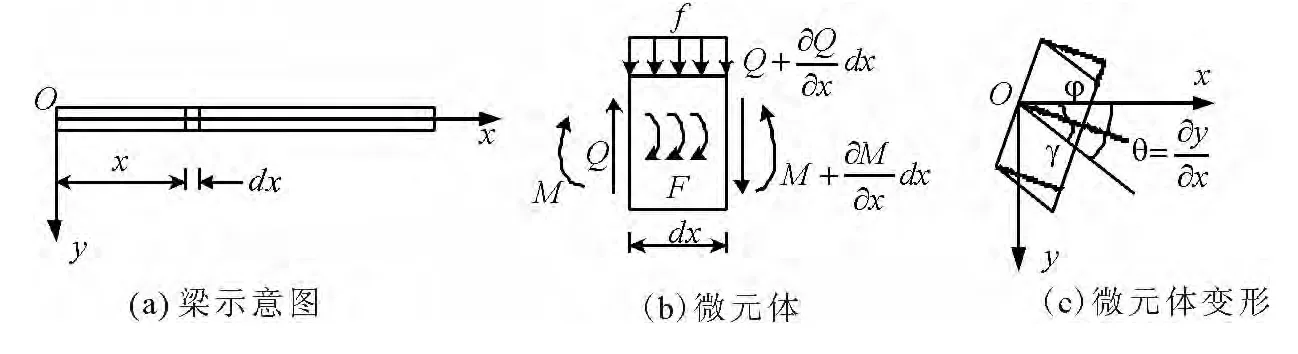
图1 梁及微元体受力图

1 Timoshenko梁自由振动方程[1]

如图1(a)所示为xy平面内的等截面梁，图1(b)和图1(c)分别为梁一段微元体的受力平衡图以及变形图.设梁的横向位移y(x，t)可以表示为

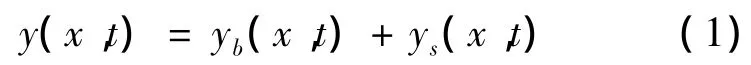
式中yb和ys分别为弯曲变形和剪切变形.截面的转角为

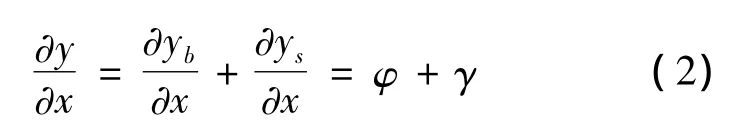
其中φ和γ分别为弯曲变形和剪切变形引起的转角.根据微元体的平衡可得方程

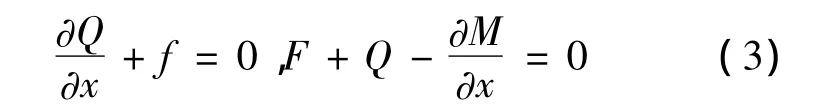
其中F为单位长度的惯性力偶.又由材料力学知识得

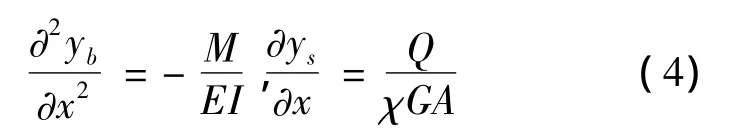
由式(2)，(3)和(4)可得梁的自由振动平衡方程为

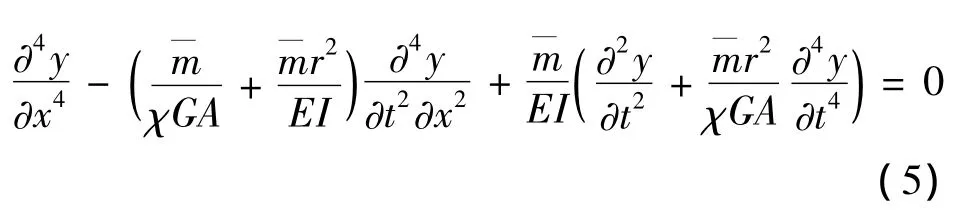
设 y(x，t)= φ(x)sinωt，代入上式整理得

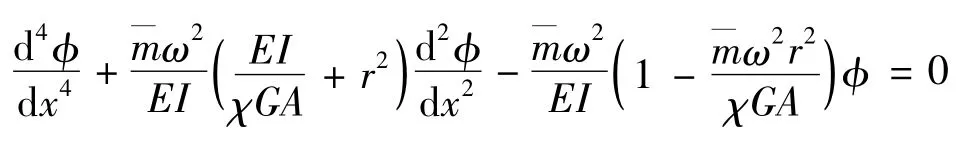
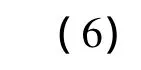
定义下列变量将上式无量纲化

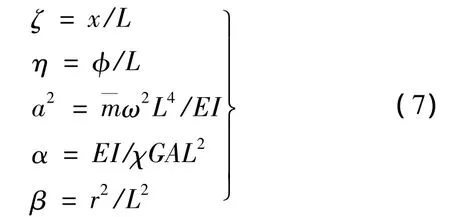
L为任意具有长度量纲的常量.将(7)式代入方程(6)则

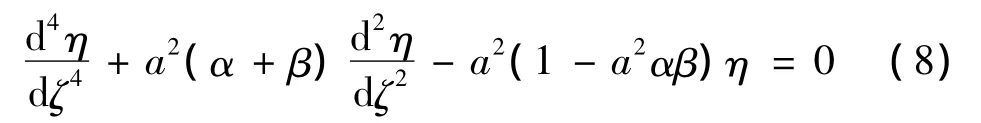
方程中，a是一个与梁振动频率平方成正比的量;α与梁的剪切刚度成反比;β与转动惯量成正比.若，α=0表明梁的剪切刚度无穷大，剪切变形可以忽略;β=0则表明转动惯量可以忽略.

2 悬臂梁振型求解及变形分离

令 η =Aeλζ代入(8)式得

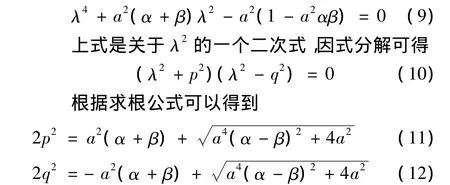
从式(11)可得到p2为非负值.方程(11)的其中两个根为 λ1，2= ± ip;又p2q2=a2(1 － a2αβ)，因为p2为非负值，则q2与1－a2αβ同号.为了简单起见，不考虑1 －a2αβ ＜ 0的情况.所以λ3，4= ±q，最终得到通解

则由于式(13)、(15)、(16)和(17)可得

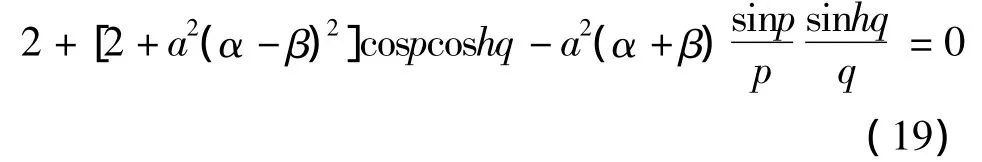
求解上面的超越方程，可得到与频率相关的梁a，进而可以得到无量纲化的振型函数

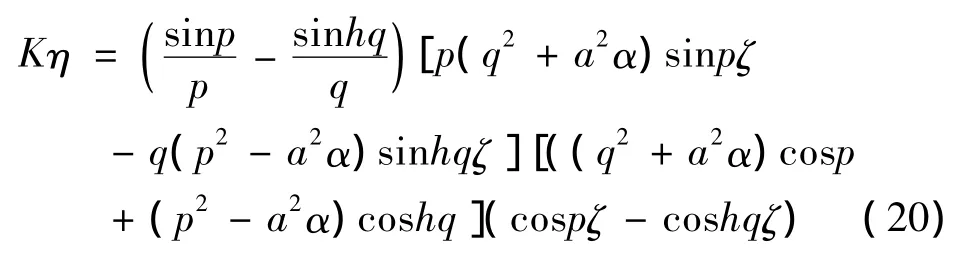
式中K为任意常数.将(16)式两边同时乘以EI/χGAL2，并利用(4)式可得

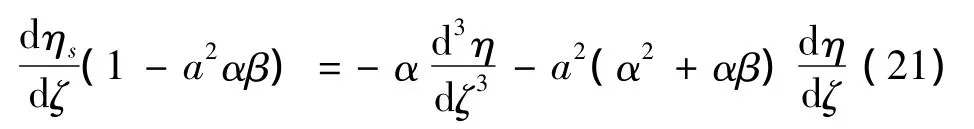
将上式两边对ζ在[0，ζ]间积分可得振型中剪切变形表达式为

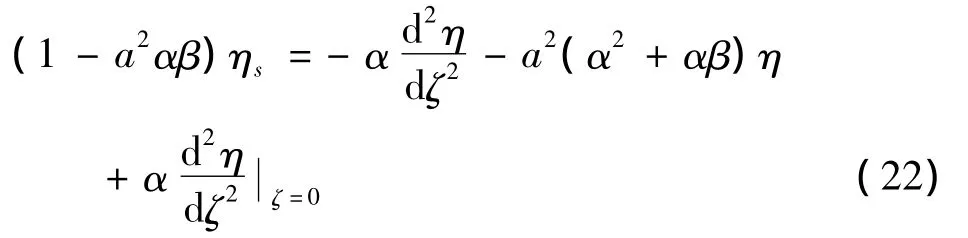
用总的变形η减去剪切变形可得振型中的弯曲变形表达式

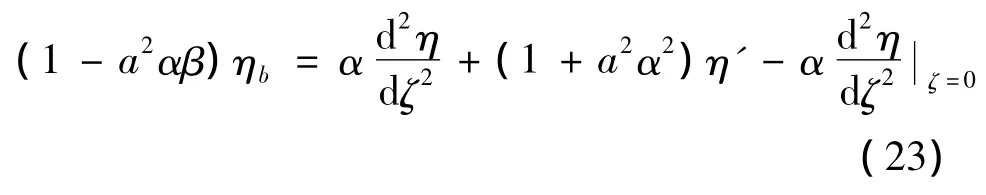
3 悬臂梁振型求解及振型分离

悬臂梁按某一振型振动时，梁中储存的弯曲应变能和剪切应变能分别为

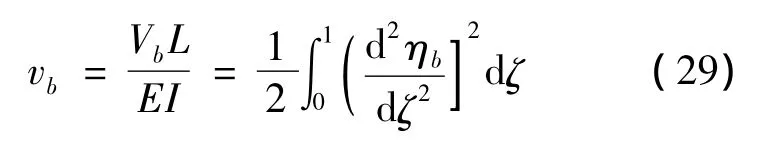
4 算例分析

假设有4m长的矩形悬臂钢梁，截面宽度0.2m，高0.4m，弹性模量 E=210GPa，G=80GPa.可得，β =0.00083，α =0.0026.通过数值计算得到悬臂梁前九阶的频率、对应振型以及剪切应变能和弯曲应变能见表1，并将这些数据与对应欧拉梁进行了对比.从表中的数据可以看出，频率较低时，欧拉梁和铁木辛科梁的频率相接近，且剪切变形能的比重也较低.高阶振型时，铁木辛科梁和欧拉梁的频率相差较大，剪切变形影响很大，剪切变形能占总变形能不可忽略.梁的前四阶振型如图2所示，图中还给出了弯曲变形分量和剪切变形分量.从图中可以看出，随着振型阶数的提高，剪切变形分量越来越明显.当改变梁的长度时，观察梁的一阶振型中剪切分量和弯曲分量的变化如图3所示.当梁长度由4m变为0.5m的过程中，梁的剪切变形分量越来越明显，相应的剪切变形能占总应变能比重也会越来越高..

图2 梁各阶振型(T－总变形，B－弯曲变形，S－剪切变形)

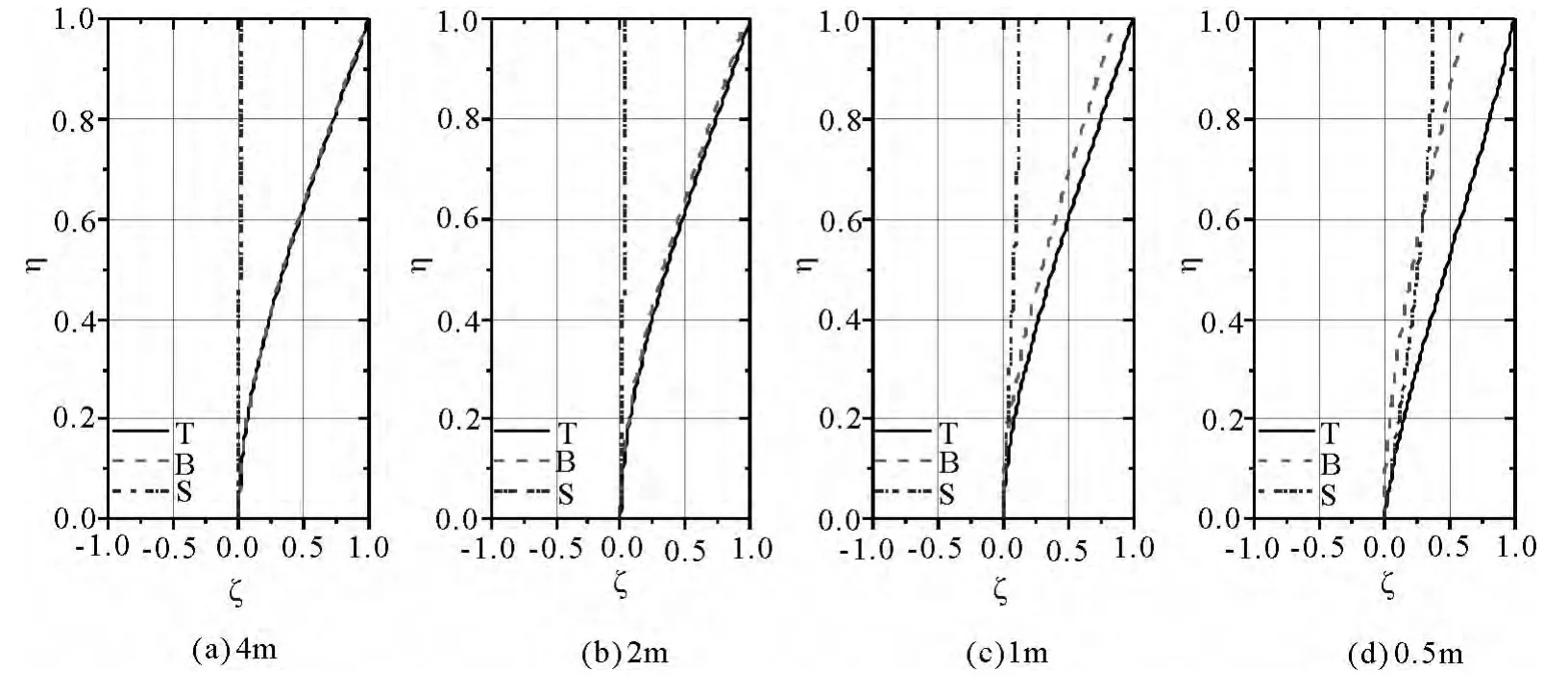
图3 不同长度梁一阶振型(T－总变形，B－弯曲变形，S－剪切变形)

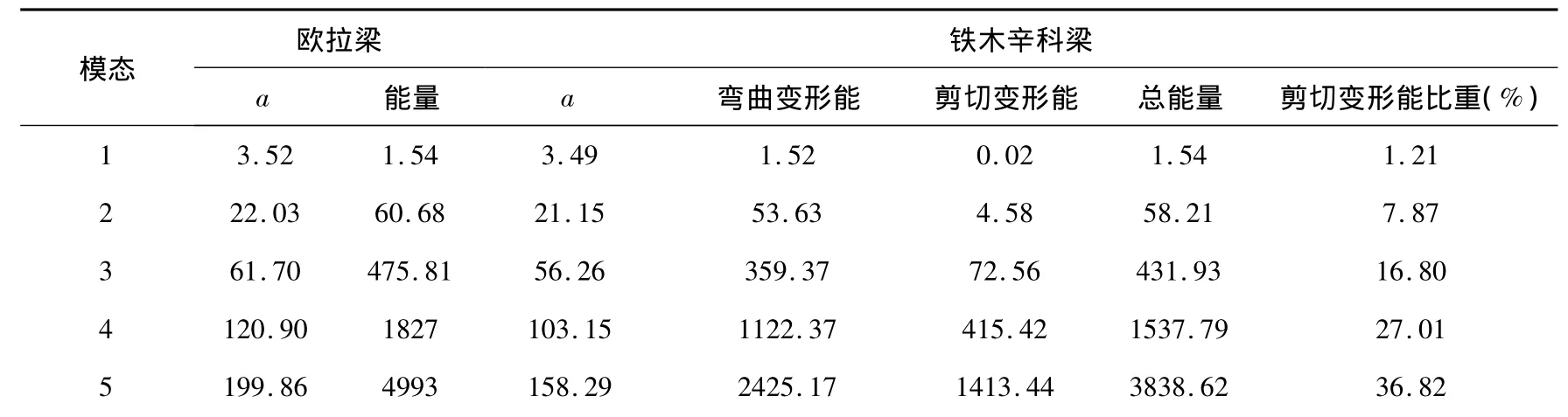
表1 铁木辛科梁主要计算参数及与欧拉梁对比

6 298.56 11142 218.67 4211.43 3531.76 7743.19 45.617 416.99 21735 282.23 6347.29 7218.99 13566.28 53.218 555.17 38526 347.57 8676.89 12846.93 21523.82 59.699 713.08 63563 413.79 11060.13 20685.39 31745.52 65.16

5 结论

本文通过对考虑剪切变形的悬臂梁的振型和能量分析发现，随着梁长细比的减小以及振型阶数的提高，振型中剪切变形分量越来越明显，剪切应变能占总应变能力的比例越来越高.

[1]Traill－Nash R W，Collar A R.The Effects of Shear Flexibility and Rotatory Inertia on the Bending Vibrations of Beams[J].The Quarterly Journal of Mechanics and Applied Mathematics，1953，6(2):186－222.

[2]Huang T C.The Effect of Rotatory Inertia and of Shear Deformation on the Frequency and Normal Mode Equations of Uniform Beams with Simple end Conditions[J].Journal of Applied Mechanics，1961，28(4):579 －584.

[3]楼梦麟，任志刚.Timoshenko简支梁的振动模态特性精确解[J].同济大学学报:自然科学版，2002，30(8):911－915.

[4]陈镕，万春风，薛松涛，等.Timoshenko梁运动方程的修正及其影响[J].同济大学学报:自然科学版，2005，33(6):711－715.

[5]蒋济同，王熙堃.一种推导 Timoshenko梁频率方程的新方法[J].中国海洋大学学报:自然科学版，2009，38(6):1035－1039.