基于分块PCA的眉毛识别方法研究①

李颜瑞， 杨 毅

(1.山西机电职业技术学院信息与管理工程系，山西长治 046011;2.中北大学电子与计算机科学技术学院，山西太原 030051)

0 引言

经过无数人的研究和实验，生物特征识别技术已经被公认为安全系数较高的身份验证方法.到目前为止，生物特征研究基本上已经涵盖了人类的所有的特征.比如:掌纹[1]，指纹[2]，人脸[3]，虹膜[4]，眉毛[5]等生物特征.其中有一些特征识别技术已经得到应用，例如指纹、掌纹和人脸.虽然其它生物特征暂时还没有得到应用，但是这些生物特征仍然具有很大的应用潜力和研究价值.所以，本文继续研究利用眉毛特征进行识别.主成分分析即PCA方法，是利用通过建立子空间进行识别得.但是在应用主成分分析时，通常是对图像整体进行主成分分析[6]，保证了整体特征信息的完整，而忽略了局部特征信息和细节特征信息.所以，本文决定采用分块PCA方法进行眉毛识别.

1 PCA理论

PCA也称为主成分分析[7]，被广泛地应用到模式识别中，是大家公认的一种识别效果相对较好的识别方法，该方法是利用线性分析方法进行识别.Turk和Pentland首先提出了主成分分析方法，是利用K－L变换实现得，该变换能将原图像数据或者原音频数据降低维数并且图像或者音频所包含的有用信息却没有减少，其降低维数的方法是利用求最小均方误差值得到的，是一种应用范围最广的特征提取方法.工作原理如下:

例如存在一个矩阵w，其矩阵大小为n×m，则可以将该矩阵表示为m个，n维的列向量，即w={x1，x2，…，xm}，则可以求出矩阵 w 的协方差矩阵Cw为:

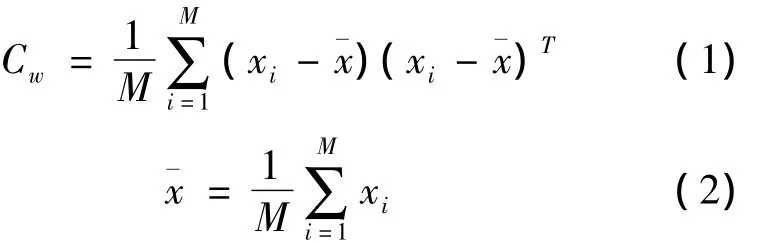
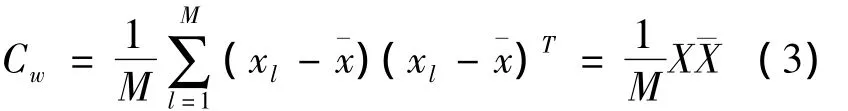
那么这样计算得到的协方差矩阵Cw就为一个n×n的方阵.从理论上讲可以直接对协方差矩阵Cw进行特征分解，求取特征值和特征向量.但是这时，协方差矩阵Cw的维数很大，直接求特征值和特征向量必然存在很大的计算量和困难.所以，为了克服这些困难，可以先对协方差矩阵Cw进行奇异值分解.这时再求协方差矩阵Cw的特征值和特征向量就相对容易了.将分解得到的特征值λ进行从大到小的排序，即 λ0，λ1，…，λm－1，则每个特征值 λ对应的特征向量 β 为 β0，β2，…，βm－1.

通过分析发现，较大的特征值对应的特征向量能够很好的表达矩阵的信息.反之，较小的特征值对应的特征向量在表达矩阵信息的作用上，效果不大可以忽略不计.所以，可以删除特征值较小的特征向量，以达到压缩特征向量的选取的个数并且选取的个数可以由阈值η决定，即

其中k表示选取前k个较大特征值所对应的特征向量.阈值η通常取0.9.

所以，由前 k 个特征值 λ0，λ1，…，λk－1，所对应的特征向量 β0，β2，…，βk－1组成的矩阵称为特征空间即 B=(β0，β2，…，βk－1).

2 基于分块PCA的眉毛识别方法

2.1 眉毛数据库选取及预处理

眉毛数据库是用来验证识别理论是否正确的唯一的根本依据.所以，首先要建立实验所需要的眉毛数据库，同时为了保证实验的可信度，本文研究决定仍然使用北工大李玉鑑教授建立的高质量的眉毛数据库[8](图1)，同时仍然采用手工圈取的方法提取眉毛区域(图2)，利用计算机进行灰度化(图3)，并且用相应的插值算法进行归一化，本文使用双线性插值算法将眉毛图像设置为50*200像素(图4).

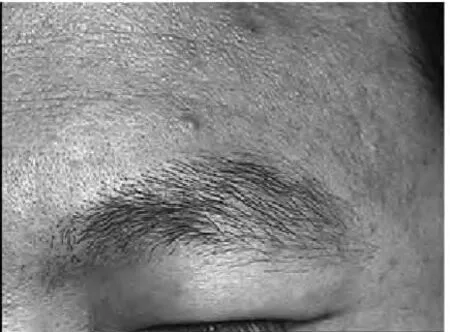
图1

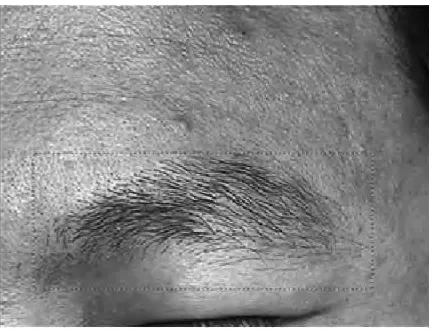
图2

图3

图4

2.2 眉毛特征提取

特征提取就是从图像中提取出能够唯一表达这类图像的信息参数.无论是在识别还是在检索，特征提取是最基础的一步，也是必不可少的一步.特征提取方法如下:

假定眉毛图像定义为Mij(1＜i，j≥n)，Mij表示第i个人第j条眉毛.共有n个人.

(1)将眉毛图像平均分成w块，且每块眉毛图像大小为h*k，则每块眉毛图像中数据用mi，j(1≤i≤h，1≤j≤k)表示.

(2)取第一个人，第一块眉毛图像w11，按照列优先的原则将第一块眉毛图像组成一个列向量，即可以表示为:

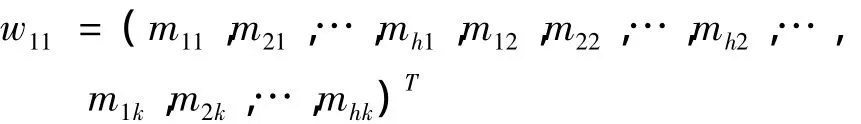
这样可以将每个人用来训练的眉毛，分块后取出第一块，按照上述方法写成列向量形式，即可以用w21，w31，…，wn1表示，则这些列向量可以组成一个新的矩阵 W1=(w11，w21，w31，…，wn1).

(3)构造矩阵W1的协方差矩阵CW1，即CW1=.其中w为协方差矩阵

2.3 眉毛识别

为了验证方法的正确性，本文依然用最近邻法则[9]进行识别，识别方法为:

(1)将测试眉毛分块后，按照特征提取方法，把每块眉毛列向量在相应的特征空间t上进行投影，得出每块眉毛的特征向量，然后将所有的特征向量按照分块顺序连接成一个行向量.就为测试眉毛的特征向量.用y测表示.

(2)计算yi之间的欧式距离的平均值和yi与y测的欧式距离.

(3)如果yi与y测的欧式距离的最小值大于yi之间的欧式距离的平均值，则可以得出结论:该眉毛为非眉毛库中的眉毛.反之可以得出结论:该眉毛为眉毛库中的眉毛，且为yi与y测与的欧式距离最小的那个人的眉毛.CW1中，行向量的平均值构成的列向量.并求出协方差矩阵CW1的特征值和特征向量，即用λi和βi表示.然后根据阈值ηi，按照特征值从大到小，选取前p个特征向量，构成特征空间.即t=(β1，β2，…，βp)T.

(4)将分块眉毛列向量在特征空间上的投影就为该分块眉毛的特征向量.即yi1=(t*wi1)T，其中1≤i≤n表示第几个人.即yi1就为第i个人的，第一个眉毛分块的特征向量，且为行向量形式.

(5)按照上述方法，可以求出每个人的其它分块的眉毛特征向量.分别用yi2，yi3，…，yiw表示.

(6)将每个人的各个分块特征向量按照分块顺序合并成一个特征向量就为每个人眉毛的特征向量.即用yi表示.

3 实验

影响本文实验的因素主要有两个:一是分块的数量、二是阈值的选取.所以实验从这两个方面进行比较验证.

眉毛库中选取109人眉毛，每人睁眼、闭眼各一张，用matlab仿真，实验的结果比较如下:

(1)确定好阈值和分块数量，比较先使用小波变换处理，在进行特征提取与直接进行特征提取对实验结果的影响.如表1所示:

表1 是否使用小波

(2)确定好阈值，比较采用不同的分块数量对实验结果的影响.如表2所示:

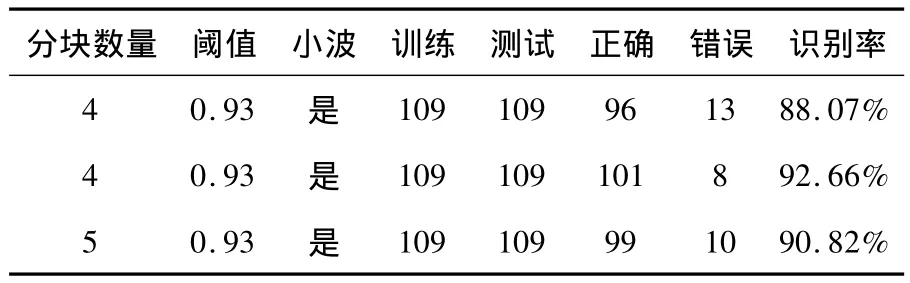
表2 采用不同的分块

(3)确定好分块数量，比较采用不同的阈值对实验结果的影响.如表3所示:

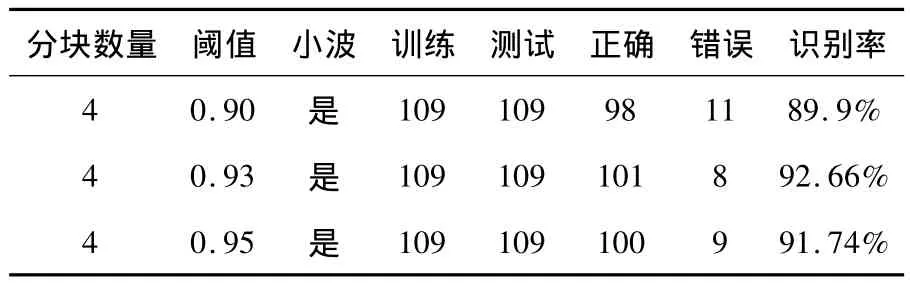
表3 采用不同的阈值

4 结束语

在109人的数据库上，通过matlab仿真实验分析，研究发现使用分块PCA进行特征提取，利用最近邻法则进行眉毛识别，识别率最高为92.66%.这样就证明了分块PCA方法进行眉毛识别是可行得，同时也证明了眉毛可以作为生物特征来识别人.然而本文的眉毛数据库直接使用的是北工大采集的数据库，从数据库中的眉毛图像可以发现，有些因素就没有考虑进去或者有些因素人为的给避免了.但是，实际应用中，这些因素是没有办法避免的，甚至对识别率影响还非常大，必须考虑到.例如，表情的不同和光照的强弱以及顺光、逆光的差别都会对眉毛图像的像素点的数值产生变化，影响识别率.所以，今后要重点研究其它因素对识别的影响.

[1]邬向前，王宽全，张大鹏.一种用于掌纹识别的线性特征表示和匹配方法[J].软件学报，2004，15(6):869－880.

[2]罗希平，田捷.自动指纹识别中的图像增强和细节匹配算法[J].软件学报，2002，13(5):946－956.

[3]周杰，卢春雨，张长水，等.人脸自动识别方法综述[J].电子学报，2000，28(4):102－106.

[4]王蕴红，朱勇，谭铁牛，等.基于虹膜识别的身份鉴别[J].自动化学报，2002 ，28(1):1－10.

[5]李玉鑑，谢欢曦，周艺华.基于2DPCA的眉毛识别方法研究[J].武汉大学学报，2011，57(6):517－522.

[6]李玉鑑，王利娟.基于PCA的眉毛识别方法研究[J].计算机工程与科学，2008，30(11):28－30，37.

[7]胡长勃，冯涛，马颂德，等.基于主元分析法的行为识别[J]，中国图像图形学报，2000，5(10):818－824.

[8]http://mpccl.bjut.edu.cn/EyebrowRecognition/BJUTEyebrow-Database/BJUTED.html.

[9]边肇棋，张学工等.模式识别(第二版)[M].北京:清华大学出版社，2000.