基于BP神经网络的小样本失效数据下继电保护可靠性评估

戴志辉，李芷筠，焦彦军，王增平

（华北电力大学 电气与电子工程学院，河北 保定 071003）

0 引言

继电保护作为电力系统的第一道防线，其自身的高可靠性是电力系统正常运行的基本保证［1-2］。目前对于继电保护的可靠性评估主要从保护的原理失效、软硬件失效、人为因素等角度出发进行分类分析［3-4］。常用的评估方法如 Markov 模型法［5］、故障树 法［6］、GO 法［7］及可靠性工程 数据分析方法［8］等对于失效数据量都有一定要求。微机保护和全数字化保护系统的应用极大提高了继电保护运行的可靠性，极少的运行失效数据也给保护可靠性评估增加了难度。在高可靠性继电保护系统中直接应用上述方法，可能会出现较大误差，难以正确反映保护的实际运行状况，若作为检修及改进设计的依据可能会造成更大损失。本文基于保护系统实际运行数据，针对高可靠性继电保护系统特性，研究适用于小样本失效数据的可靠性评估方法，在反映保护系统各种失效模式的同时有利于进一步提高评估的精度。

对于继电保护小样本数据的可靠性评估，可从扩大样本容量和采用适合小样本数据的分析方法两方面着手。目前，国内外已开展了一系列适合小样本的分析方法研究，如文献［9］提出一种贝叶斯方法，可结合小样本下多种来源、多种形式的先验信息，得到较完整的后验信息，不需很大的子样也能得到较好的概率估计值。但在贝叶斯统计推断方法中，不同形式的验前分布将引起不同的统计分析后果，对于贝叶斯估计将产生不同的风险。而且由于继电保护运行的特殊性，其先验信息非常少，这也给评估带来很大难度。文献［10］利用Bootstrap方法将小样本问题转化为大样本问题来估计负荷模型参数的近似分布，该方法对于经验分布的选取和样本数量的大小存在一定依赖。文献［11］通过实例说明了小子样下Bootstrap方法仿真可能带来很大偏差。文献［12］对蒙特卡罗方法进行了阐述，该方法是基于概率统计理论的一种随机抽样方法，比较简单且容易实现，但方法的有效性取决于所建立的数学模型及输入信息。加之以上方法对于原始数据的分布模型有较大依赖，若选取的分布模型有误，可能无法进行正确、有效的后续评估。根据小样本数据无法确定可靠性数据的分布模型，也成为影响可靠性评估效果的重要因素。此外，支持向量机（SVM）理论在小样本数据的回归估计和可靠预测等研究中也得到越来越多的应用，它是一种基于结构风险最小化原则的机器学习方法，在解决小样本情况下的回归问题方面展现了良好的学习性能。例如文献［13］采用SVM回归代替最小二乘法进行数据拟合，进而通过威布尔分布进行可靠性分析，在小样本数据情况下，得到了较好的曲线拟合结果。但SVM对噪声或野值敏感的问题仍待进一步解决，其用于继电保护可靠性分析时，需要考虑小样本数据存在的分散性、核函数选取对SVM方法回归精度和泛化能力的影响。神经网络具有较好的自学习、自组织和自适应性能力，且其结构特征决定了它具有较强的容错能力，允许输入样本中带有较大的误差甚至个别错误，对于扩充数据样本能够实现较好的仿真［14］，有利于减小本文所提方法的误差。

综上，结合高可靠性继电保护系统运行的特点，提出一种基于BP神经网络的小样本失效数据下继电保护可靠性评估方法。该方法通过已有的小样本失效数据，根据经验公式计算其可靠度作为BP神经网络的输入，将失效数据作为输出，对BP神经网络进行学习训练，并用训练后的模型对小样本数据进行扩充。利用扩充的数据样本进行可靠性评估，较好地解决了分布模型的选取问题，且能有效提高评估效果和精度，为解决小样本数据下继电保护系统可靠性评估提供了新的思路。

1 继电保护可靠性分布模型

对于继电保护装置的可靠性评估，目前采用的失效分布模型主要包括指数分布模型和威布尔分布模型等连续型分布模型。

指数分布可分为单参数指数分布和双参数指数分布，双参数指数分布比单参数指数分布多一个位置参数γ，下面给出其分布函数。

故障概率密度函数：

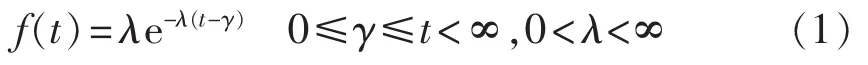
可靠度函数：

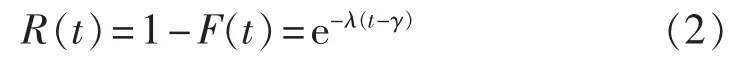
其中，t为时间；λ为指数分布的失效率，是一个与时间无关的常数，可用来描述设备的偶然失效，对应“浴盆曲线”的盆底段；位置参数γ表示分布函数的起始时刻。

威布尔分布近年来在可靠性设备寿命分析中得到了广泛应用，它对各种类型的数据拟合能力较强，可较全面地描述产品不同失效期的失效过程与特征。且当威布尔分布的形状参数m=1时，它退化为指数分布；当参数mϵ［3，4］时，其分布接近于正态分布。威布尔分布有两参数威布尔分布和三参数威布尔分布，这2种分布在失效率函数、故障概率密度函数、可靠度函数等方面具有相似性。一般在可靠性分析过程中两参数威布尔分布模型应用较多，下面给出其函数［15］。

故障概率密度函数：

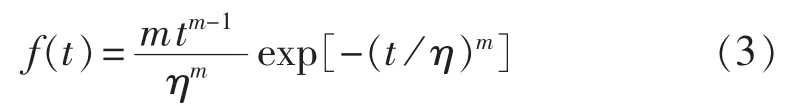
失效率函数：

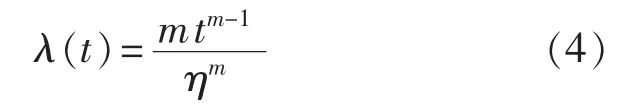
可靠度函数：

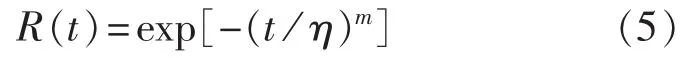
其中，t为时间；m为形状参数；η为刻度参数。

由于在继电保护可靠性评估过程中，选取的设备失效分布模型在很大程度上决定了评估效果［16］，因此有必要科学地确定其失效分布模型。对于小样本失效数据，由于其特征不明显，不论采用指数分布还是威布尔分布都能得到较好的拟合结果［17］，却可能无法真实反映继电保护失效本身的特性。本文在扩充失效样本的基础上通过最小二乘法拟合中的相关系数区分和确定哪种分布更适合待分析继电保护系统的失效特征。

2 BP神经网络模型

2.1 神经网络原理

神经网络是对人的神经系统的模拟，由于BP神经网络具有较好的函数逼近能力［18-19］，本文采用BP神经网络对高可靠性继电保护小样本失效数据进行模拟仿真完成数据扩充。

BP神经网络基本结构见图1。BP神经网络由输入层、隐层和输出层构成，每个神经元将加权后的输入与阈值（偏移）向量代数求和后得到各自的输出。

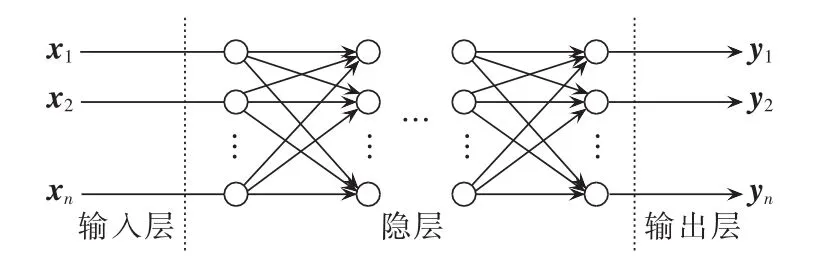
图1 BP神经网络Fig.1 Schematic diagram of BP neural network

利用BP神经网络仿真主要分为以下几个步骤。

a.构造网络模型，包括确定输入/输出数据形式、网络层次及传递函数形式。

b.网络学习训练，确定权系数和阈值参数。

c.利用网络进行仿真。

2.2 BP神经网络模型及学习训练

BP神经网络的传递函数必须可微，为了尽量减少仿真误差，本文采用2层模型，输入层神经元采用log-sigmoid型传递函数logsig，输出层采用线性传递函数purelin。

BP神经网络的训练利用误差反传原理，不断调整网络的权值使网络模型输出值与已知的训练样本输出值之间的误差平方和达到最小或小于某一期望值。本文采用梯度下降动量BP算法进行BP神经网络的学习训练，该算法的学习速率是自适应的，且网络训练误差较小，能得到较好的数据仿真结果。

3 基于BP神经网络的继电保护可靠性评估

BP神经网络方法用于小样本数据的可靠性评估，一方面能减小对分布模型的依赖，从而达到减小评估误差和不确定性的效果；另一方面可通过扩大数据样本更准确地判别分布模型。基于BP神经网络的可靠性评估过程如图2所示。

3.1 基于BP神经网络的继电保护可靠性数据样本扩充

设有N台继电保护装置的失效数据t1、t2、…、tr（r＜N），且 t1≤t2≤…≤tr，其中，样本数据容量 r≤10。

图2 基于BP神经网络的继电保护系统可靠性评估流程图Fig.2 Flowchart of relay protection system reliability assessment based on BP neural network

在未知数据样本的分布模型的情况下，可以通过经验分布函数估计出经验可靠度作为BP神经网络的输入。但经验分布函数在样本容量较小时会有较大的计算误差，为减小误差，在小样本情况下，可采用下列公式计算经验可靠度［14］。

海森公式：

近似中位秩公式：

数学期望公式：

式（6）—（8）各有其适用性，对不同分布模型的参数估计，其误差不同。因此有必要在使用经验公式时对其进行误差校验，力求挑选出最适合数据样本分布模型的经验公式，以减小评估误差，提高评估效果。本文将通过算例说明当分布模型选取为威布尔模型时，近似中位秩公式误差最小；当分布模型选取为指数分布时，数学期望公式误差最小。

对于原始小样本失效数据，按经验公式可计算出其对应的可靠度值 R（ti），并将向量｛R（t1），R（t2），…，R（tr）｝作为 BP 神经网络的输入，将｛t1，t2，…，tr｝作为BP神经网络的输出，对BP神经网络进行学习训练，以优化确定网络内部的结构参数，即权参数和阈值参数，一旦参数得到确定，即可应用该网络模拟生成新的可靠性数据。训练样本少会对BP神经网络的训练产生一定影响，因此本文未直接使用BP神经网络对可靠度或失效时间等指标进行预测，而是首先针对原始数据样本，利用BP神经网络仿真得到与原始数据样本变化规律近似的扩充数据，然后采用基于最小二乘法的威布尔分布模型进行参数估计，较直接进行可靠性指标计算而言，拟合误差要小。

由BP神经网络的特性可知，网络模拟生成的新的可靠性数据与原始数据有近似的规律和特性，且样本量的扩大减小了偶然因素，一定程度上避免了因对分布模型的依赖而造成的误差，甚至错误评估。

3.2 基于扩充数据样本的保护可靠性评估

由于BP神经网络仿真模拟生成的扩充数据样本与原始数据样本具有相同的变化规律，可利用BP神经网络模拟生成的可靠性数据及其对应的可靠度，分别对指数分布和威布尔分布模型进行最小二乘法参数估计，计算出各模型的参数值；并根据最小二乘法的相关系数ρ确定扩大的数据样本的分布模型，即相关系数ρ的绝对值越接近于1，这组数据越符合该分布模型。

通过比较指数分布和威布尔分布模型的相关系数ρ的绝对值与1的接近程度，对该样本数据的分布模型进行区分和确定，解决了因数据样本少而无法选择最适合的分布模型的问题，也间接提高了参数估计的精度。

确定分布模型并得到各参数后，即可利用第1节所示各分布模型的可靠度函数计算可靠性指标。

4 算例分析

选取某一型号的继电保护装置50台，在同样的操作水平和工况下，记录它们各自的投入运行时间和发生故障的时间，如表1所示，选取装置最后的故障时刻2007-12-25T09-00为截止时刻。

表1 继电保护系统运行数据记录Table 1 Operational data records of relay protection system

将正确动作的数据滤除，然后按照设备运行的时间长短排序得到失效数据样本，即：t1=4399 h，t2=5862 h，t3=9582 h，t4=9606 h，t5=13327 h，t6=16158h，t7=17622 h，t8=20407 h。分别采用海森公式、数学期望公式、近似中位秩公式计算其对应的经验可靠度值如表2所示。

分别将海森公式、数学期望公式、近似中位秩公式对应的向量 R1（ti）、R2（ti）、R3（ti）作为 BP 神经网络的原始输入，将失效时间组成的向量T作为其各自的输出，通过MATLAB程序实现BP神经网络的学习、训练，训练误差小于0.001时，训练结束。向量R1（ti）、R2（ti）、R3（ti）和 T 分别为：

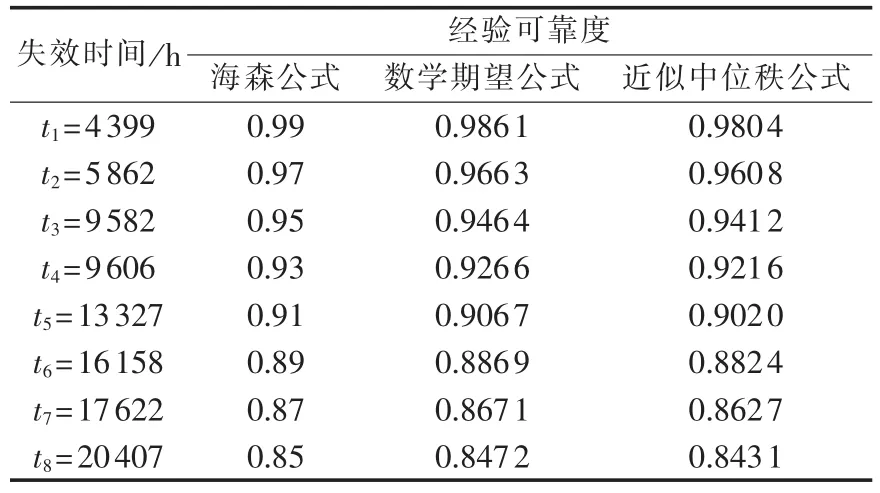
表2 经验可靠度Table 2 Experience reliability

为了获得较好的仿真估计效果，可根据原始输入可靠度值的范围大致确定仿真输入的范围，扩充数据样本量也可以根据实际需要确定。本算例为了得到样本量为50的扩充数据样本，将0.8～1范围内的50个随机数按从大到小的顺序排列成向量，输入已经训练完成的BP神经网络进行仿真，得到50个新的失效数据，作为原始数据的扩充样本。

对扩大数据样本，分别采用最小二乘法进行指数分布和威布尔分布参数估计，其结果如表3所示。

分析各经验公式下的各分布模型参数估计结果可得以下结论。

a.最小二乘法曲线拟合的相关系数ρ反映了原始数据与所拟合分布模型的符合程度，整体比较指数分布和威布尔分布模型的曲线拟合相关系数可知，指数分布最符合该原始失效数据的失效分布模型，威布尔分布其次。

b.比较指数分布和威布尔分布模型的参数估计曲线拟合结果可知，其原始数据样本与扩充数据样本之间的参数估计误差都较小。但指数分布模型和威布尔分布模型在不同的经验公式下，其参数估计误差大小略有差异。威布尔分布模型在近似中位秩公式下，其扩充数据样本与原始样本的参数估计最接近，而指数分布在数学期望公式下的扩充数据样本与原始样本参数估计的误差最小。

c.比较近似中位秩公式下的威布尔分布模型和数学期望公式下的指数分布模型参数估计的原始数据与扩充数据样本的曲线拟合相关系数可知，扩充数据样本的相关系数相比原始数据的相关系数更接近于1，说明扩充数据样本比原始数据样本能得到更好的曲线拟合效果，参数估计也更精确，可靠性评估效果更好。

表3 最小二乘法参数估计结果Table 3 Results of parameter estimation by least square method

5 结论

本文结合高可靠性继电保护装置失效数据的小样本特点，采用BP神经网络对原始数据样本进行扩充，并根据扩充数据样本进行可靠性评估，既在一定程度上克服了因原始数据样本过小而影响评估效果的问题，也能减少对分布模型的依赖和评估的偶然性，从而达到对小样本数据进行有效评估的目的，算例分析结果验证了其有效性。本文研究可得出如下结论。

a.指数分布和威布尔分布可以作为继电保护可靠性评估的分布模型，这与继电保护装置的失效特性曲线——浴盆曲线是相符的，且对于分布模型的判别和选取，可以根据各分布模型的最小二乘法曲线拟合的相关系数来实现。

b.为了尽量减少扩充数据样本的误差，选择合适的经验公式很有必要。分布模型选取为威布尔模型时，近似中位秩公式误差最小；分布模型选取为指数分布模型时，数学期望公式误差最小。

c.BP神经网络模型仿真方法作为小样本数据扩充数据样本的方法有其优势，这是由BP神经网络模型本身的特性决定的。一方面BP神经网络能避免失效数据分散性、分布模型选取失误导致的评估误差；另一方面，扩充数据样本与原始数据样本的变化规律基本相同，可作为可靠性指标参数估计的参考数据。