发电成本最小化的电动汽车分布式充放电控制

邵成成，王锡凡，王秀丽

（西安交通大学 电力设备电气绝缘国家重点实验室，陕西 西安 710049）

0 引言

电动汽车在环境保护和保障能源供应安全等方面有着传统汽车无法比拟的优势，受到了广泛关注［1-2］。电动汽车的大规模使用产生的充电负荷将对电力系统运行产生深刻影响。20世纪80年代的研究已表明当时的电网难以满足不加控制的电动汽车充电需求［3］。近年来，美国等地的多项案例研究也对此做了进一步证实［4-5］。充放电控制是抑制充电负荷对电网不利影响和保障系统供电的有力措施。同时，电动汽车具有一定储能能力，为电力系统提供了丰富的可控资源，开展充放电控制能够实现负荷调度，促进可再生能源电力吸纳，产生多种效益［6-7］。

为发挥充放电控制效益，研究人员从不同层面对充电控制策略进行了讨论［8-12］。在输配电网层面，尽管诸多文献［11-14］利用集中控制模型对充放电控制平滑负荷曲线、降低发电成本的效益进行了分析和测算，但由于电动汽车数量众多、约束条件复杂，集中控制模型难以给出完全满足电动汽车约束和用户使用需求的控制方案。相比而言，分布式框架下，用户可以根据出行计划借助充放电管理设备对充电过程优化。分布式控制能够利用用户对自身出行计划的了解，在相对确定的条件下实现优化，充分满足电动汽车使用约束。同时，它仅要求用户上报充放电功率曲线而无需上报电动汽车物理参数和出行计划，在保护用户隐私方面也极具优势。采用分布式方法还可以避免对容量差别很大的发电机组和电动车辆同时优化，避免病态问题的出现。

如何协调大规模电动汽车的充放电过程、优化系统运行、降低发电成本是该类分布式控制的核心问题。文献［15］提出了充电站层面的分布式控制方法，使购电费用最小。基于博弈论分析，文献［16］提出了一种能用于充电控制使负荷波动最小的分布式方法。文献［17］则构造了一种基于凸分析的分布式控制的迭代过程，可扩展至充放电控制、追踪风电变化等问题；但该方法中，单一车辆的控制问题与电动汽车数量有关，当电动汽车数量较大时，单一车辆问题病态化，会影响方法的可用性。归结地讲，这些研究具有以下几点局限：不能处理有耦合约束的问题，仅考虑电动汽车间的相互协调，忽略了电动汽车与发电机组间的协调；仅能解决负荷波动平抑等凸问题，不能直接优化具有非凸性的发电成本；对大规模电动汽车的适应性不强，或功能有限、使用条件局限，或可处理的电动汽车数量有限。

针对此，本文提出了一种基于拉格朗日松弛LR（Lagrangian Relaxation）的分布式充放电控制机制，协调电动汽车与发电机的运行，降低系统发电成本。考虑到拉格朗日乘子数目对收敛性的影响，本文尚未计及线路传输容量约束。

1 分布式充放电控制方法

与集中式控制中调度机构直接下达充电指令不同，分布式控制中，调度机构根据系统运行状况发出调度信号，用户接收调度信号优化充放电过程、确定充放电曲线，并上报调度中心。当电动汽车数量较多时，充放电策略会对电力系统运行状态产生显著影响，因而需要进行多步迭代产生恰当的调度信号。图1给出了分布式充放电控制的一般流程。需要指出的是，当系统规模较大、电动汽车数目较多时，可设置电动汽车聚集体层，构成树状的调度系统，减轻调度中心的通信和数据汇总压力。

电价（发电、辅助服务的边际成本）信号能反映电能供需状况，用户通常也以用电费用最省为充放电控制目标，因而电价信号是一种理想的分布式充放电控制信号。当电价信号与采用集中式最优充电控制的电价接近时，表明2种控制下电力系统运行方式接近，分布式控制的效果与集中式控制效果接近。

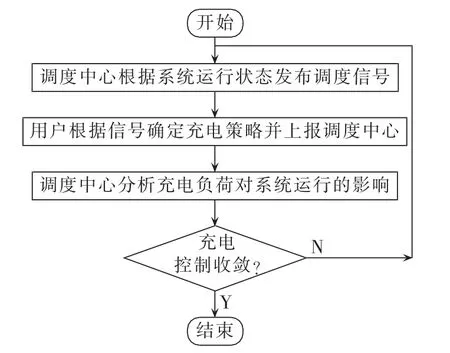
图1 分布式充放电控制的一般流程Fig.1 Flowchart of decentralized charge/discharge control

直接采用上一次迭代产生的电价作为本次迭代中的调度信号会导致用户充放电曲线振荡、迭代过程不收敛，此现象在文献［16］的研究中已得到证实，不再赘述。从流程上看，促进迭代过程收敛可采用以下2种方法：在迭代过程中采用恰当的电价信号修正方法；调整用户的优化目标。文献［16］、［17］从后一种思路出发，分别在用户优化目标中加入表示本次迭代充放电功率偏离上一次迭代所有用户平均或自身充放电功率的项，保证问题收敛。本文从前一种思路出发，基于LR、采用次梯度法对电价信号进行修正。

2 充放电控制模型

发电成本是衡量电力系统生产经济性的重要指标，此处以日发电成本最小为优化目标：

其中，fi、si分别为发电机组燃料成本函数和机组启停成本；pi，t、ui，t分别为 t时刻机组 i的发电功率和启停状态。

电动汽车充电控制过程中需满足以下约束。

a.系统约束。

系统约束包括功率平衡约束和备用约束，如下所示：

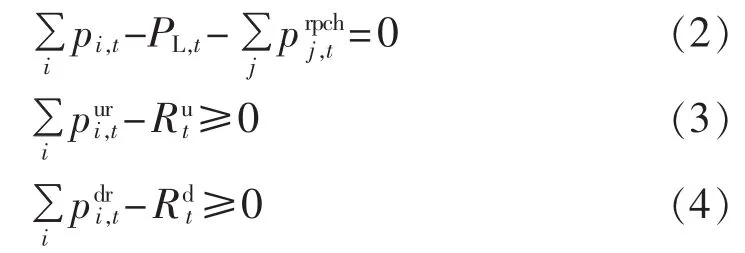
其中，PL，t为 t时刻不计充电负荷时的系统负荷；分别为机组i可提供的向上、向下备用容量；为t时刻电动汽车j的并网功率；分别为t时刻系统向上、向下备用容量的需求，取决于负荷波动和机组停运等因素。

b.机组约束。

发电机组约束包括机组最大/最小出力、爬坡速率、连续开停机时间以及开机后第一小时和停机前最后一小时出力水平等，与机组组合UC（Unit Commitment）问题类似，不再赘述。

c.电动汽车约束。

受出行需求限制，仅能在电动汽车未出行的并网时段内进行充电控制。设电动汽车j在tarr时刻结束上一行程、并入电网，此时电动汽车的荷电状态为SOCj，arr；电动汽车在 tdept时刻出发，出行过程中所需能量为用户出发时所需的荷电状态SOCj，dept为：

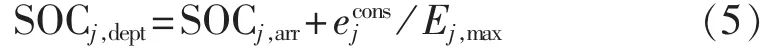
其中，Ej，max为电动汽车的储能容量。

在tϵtplug=［tarr，tdept］的时段范围内进行充放电控制（以下各式的t均在此范围内）。仅考虑充电过程时，电动汽车需满足充电电量约束和充电功率约束，如下所示：

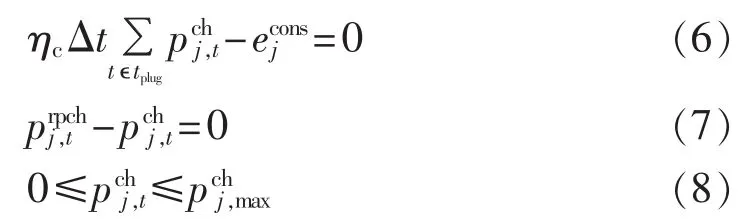
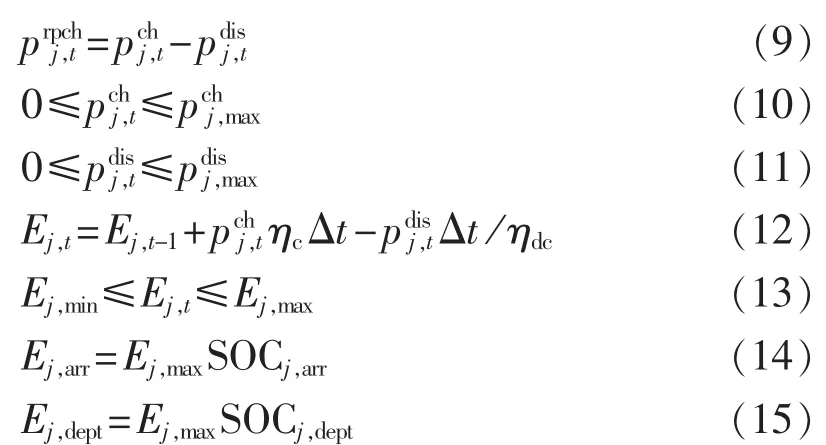
其中，Ej，t和分别为 t时刻末电动汽车 j的储能水平和 t时刻的放电功率；Ej，arr和 Ej，dept分别 为到达 和出发时刻电动汽车j的储存能量；ηdc和Ej，min分别为放电效率和最低储能水平；为最大放电功率，可由以及充放电效率折算得到。

当以供电成本或充放电费用为优化目标时，考虑充放电效率，电动汽车不能同时充放电的约束可以自然满足，模型中未将其列出。式（5）—（15）给出了单一电动车辆在一个并网时段中的充放电控制约束。用户多次出行会将研究周期分割为多个并网时段。它们可以通过出发时刻荷电状态SOCj，dept、行驶过程中耗能以及到达时刻荷电状态SOCj，arr相互关联。根据出发时间、出行距离，可以形成用户全天的充放电功率约束。

以上模型具有如下特点：机组、电动汽车受到单机约束的同时，通过系统约束相互耦合；耦合约束数目相对较少；单机约束数量与电动汽车数量密切相关。

上述模型用于系统日运行计划和用户日前充放电计划的制定，因而采用了确定性的用户出行计划数据。尽管对于系统调度人员而言，大量电动汽车的整体出行行为具有一定的随机性和不确定性，但对单一用户而言，自身的出行计划却是可知的、相对确定的，如用户上下班出行时间就相对确定。从出行约束处理和出行需求满足的角度看，相比集中式（调度）控制，分布式（用户）控制充分利用了用户自身所掌握的信息，所需处理的约束更为确定，因而更具优势。

基于确定运行计划的日前充电安排，实现了充电负荷和发电机组在计划上的协调配合。用户临时的、紧急的充电需求可通过系统运行的实时调整和实时充电控制实现。

3 基于LR的分布式充放电控制方法

LR是一种大规模优化问题的分解算法，其基本思想是利用对偶因子将耦合约束松弛，将原问题转化为一个分层迭代求解的鞍点问题。下层求解一系列规模较小的子问题；上层通过对偶因子的更新实现子问题间的协调。LR在电力系统优化特别是UC中得到广泛应用［18-20］，本文方法正是以LR求解UC为蓝本的。LR可将原问题分解为单一机组优化运行和单一车辆充放电优化问题，同时，对偶因子对应于发电、备用边际价格（成本）的概念，非常适用于分布式充放电控制。

3.1 问题分解

由于 “创造”是一个含义丰富、表现形式多样的概念，因而创造力的定义也多种多样[2]。狭义的创造力是 “首创前所未有的事物的能力”。广义的创造力是“产生出一切相对于创造主体而言的、有益社会发展的新的思维、行动或结果的能力。”

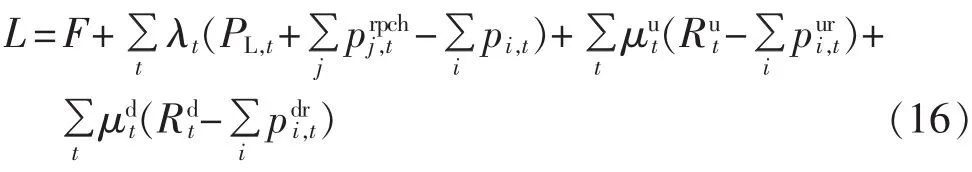
与UC类似，该对偶问题具有良好的变量分离特性，可以拆解为单机优化问题和单一车辆优化问题。下层的单机优化问题与UC中类似，而单一车辆优化问题具有如下形式：

式（17）、（18）分别描述了充电和充放电控制问题。λt由上层计算给定，此时它们为线性规划问题，可采用单纯形法、动态规划法等方法求解。

3.2 可行解构造

非凸问题的对偶最优解一般对应于原问题的非可行解。利用LR求解UC问题时，会将对偶解的整数部分（即发电机启停状态）代入原问题。原问题退化为发电经济调度问题，求解该问题得到发电机出力水平。当该组整数值不是原问题可行解时，需采用启发式方法构造原问题可行解。

电动汽车数量庞大，无法在原问题中对电动汽车充放电功率优化，因此将子问题中求得的充放电功率汇总后直接代入原问题，并采用罚函数处理功率平衡和备用约束不满足的情形。选取罚因子时，应保证罚因子大于发电或备用的边际成本。罚函数的引入可以避免迭代过程中每一步修正整数变量取值、构造原问题可行解的繁琐，只需在对偶间隙达到收敛门限、求解过程收敛后，采用已有方法进行一步可行解构造。

3.3 基于LR的分布式充放电控制流程

参照LR求解UC问题的过程，提出了基于LR的分布式充放电控制流程，如下所示：

a.选取一组初始的对偶因子（即发电和备用的边际价格）作为调度信号；

b.在给定的信号下，求解单机优化问题和单一车辆优化问题，并将结果上报调度中心；

c.调度中心根据上报信息，计算对偶问题目标函数值L和原问题目标函数值J；

d.调度中心计算相对对偶间隙dual=（J-L）/L，根据对偶间隙取值判断问题是否收敛，若收敛转向步骤e，若不收敛则更新对偶因子，转向步骤b；

e.各车辆的充放电功率即为最优功率，并可以根据对偶问题解构造可行的发电调度计划。

本文选用次梯度法进行对偶因子更新。LR对偶因子在更新过程中反映了机组启停的影响和发电成本变化情况，采用LR对偶因子作为调度信号更有利于发电成本的优化。

3.4 计算耗时分析

文中方法耗时主要发生在子问题求解、发电经济调度问题求解和信息交换环节。分布式结构下，单一车辆子问题和单机子问题并行求解，而前者（线性规划）复杂度远低于后者（混合整数规划），决定子问题求解环节耗时的单机子问题。

因而，文中方法仅比LR求解UC多出了信息交换时耗。LR求解一般UC问题的计算效率已被丰富的研究实践［18-20］证实。从计算效率和耗时角度而言，随着低延时通信设施的建设和智能电网的完善，文中方法将能够用于实际。

4 算例分析

以 IEEE-RTS1979 系统［21］为例分析，剔除了其中300 MW的水电装机，并对负荷进行等比例折算，折算后最大负荷为2550 MW。假定该系统中含有50000辆电动汽车（以全国8000万辆私人汽车、最大用电负荷500 GW进行等比例折算，电动汽车比例约为12.5%）。电动汽车划分为50个聚集体电动汽车，每个聚集体下辖1000辆电动汽车。电动汽车出行时间和出行距离的分布情况参见文献［22］，车辆类型分布如表1中数据假设。

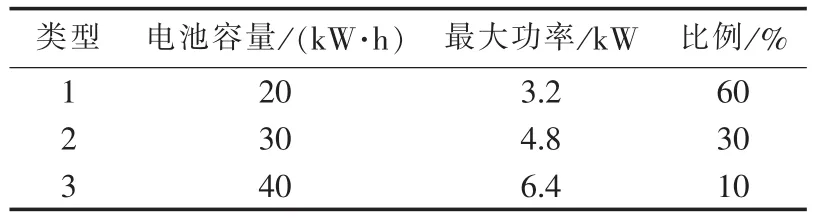
表1 电动汽车类型分布Table 1 Distribution of electric vehicle type

4.1 与已有方法对比

集中式方法可处理的问题规模有限，无法计及每辆电动汽车的充放电约束。为进行算法对比，人为构造一个电动汽车群，要求各聚集体下辖的电动汽车参数完全一致，根据相关分布抽样产生。对以下几种调度方法进行对比。

a.方法1，即集中充电调度。将第2节中电动汽车的充电约束以1∶1000放大，构成聚集体约束。得到聚集体的充放电功率后，将其均分给下辖的电动汽车。对这种下辖电动汽车参数一致的聚集体而言，聚集体满足约束意味着电动汽车也能满足相应约束。因而，集中调度是可行的，其结果可以作为最优结果衡量分布式方法的有效性。

b.方法 2，即平抑负荷波动的分布式方法［15］。通过该方法可以得到电动汽车充放电功率；将充放电功率与系统常规负荷叠加，代入UC模型可获得发电计划和系统生产成本。为避免病态问题的引入，采用本方法时也“放大”了电动汽车及其约束。

c.方法3，即本文提出的分布式方法。此时，单一车辆优化问题与电动汽车数量无关，对大规模电动汽车适应性较强，无需进行“放大”处理。

如表2所示，方法1对统一调度系统可控资源，生产成本最低；方法2、方法3成本略高于方法1。可见，分布式方法可得到近似最优的控制效果，但能处理的问题规模却远大于集中式方法。同时，与方法2类似，方法3对充电控制和充放电控制都有较好的适用性。

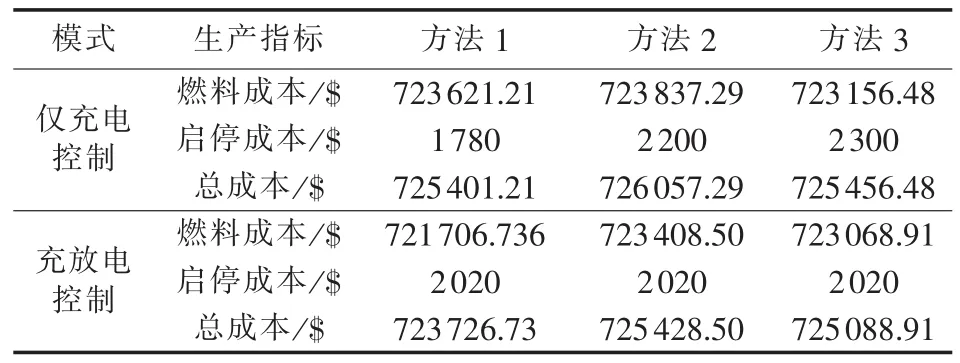
表2 人工构造电动汽车群的发电成本Table 2 Generation cost considering artificial EV group

与方法2相比，方法3不仅考虑了电动汽车间的协调，而且考虑了电动汽车与发电机组的协调，因而方法3对发电成本的优化效果更为显著。火电机组的运行受连续开停机时间、爬坡速率等跨时段约束的限制；当负荷曲线不能被完全拉平时，发电成本不仅与当前负荷水平、发电调度计划相关，而且与相邻相近的时段负荷水平和调度计划有关。方法2有利于每个时刻发电成本的优化，但不能保证一定时段内的优化。忽略跨时段的机组约束和启停成本后，方法2和方法3得到的控制方案和发电成本均十分接近。其中，方法2得到的发电成本为$677937.8，方法3为$677938.1。当可控负荷规模足够大、负荷曲线能够被拉平时，各时段运行方式差别不大，方法2和方法3优化发电成本的效果将十分接近。

4.2 仿真分析

根据相关分布，由随机抽样、模拟得到50000辆电动汽车的技术和出行参数；同一聚集体下辖的电动汽车的参数也不完全相同。电动汽车充电需求为945.62 MW·h，约占总负荷电量的1.6%。

表3为快速充电（CaseⅠ）、充电控制（CaseⅡ）和充放电控制（CaseⅢ）3种情形下系统的生产成本，其中CaseⅡ和CaseⅢ采用本文提出的方法。相比于快速充电而言，充电和充放电控制下发电成本有所降低。对一般性的大规模电动汽车群而言，本文所提出的方法依然有效。

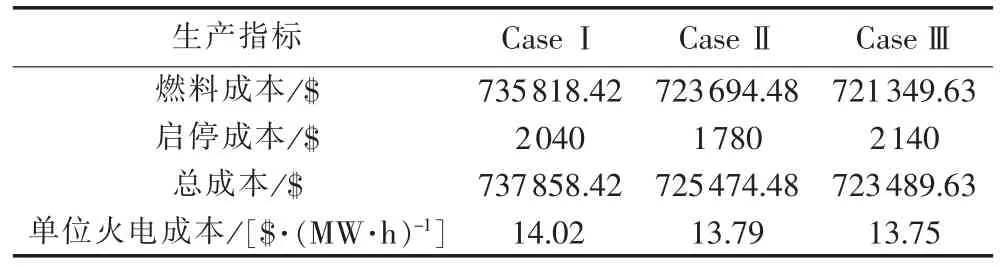
表3 不同情形下的生产指标Table 3 Production indexes for different cases

充电控制通过平抑负荷波动、减少机组启停，降低了系统发电成本。充放电控制下，尽管启停成本有所上升，但通过控制电动汽车充放电过程，可使其与发电机组协调运行，提高火电机组运行效率，降低单位火电成本，从而降低总的生产成本。

图2给出了CaseⅡ和CaseⅢ中算法的收敛过程，可见算法经过10～20次迭代即可收敛，计算效率较高。与充电控制相比，充放电控制收敛速度更快。定性地说，电动汽车放电为系统提供了更为充裕的可调度资源；系统可以调度更多资源“填补”对偶间隙。利用LR算法求解UC问题时，随着可启停的机组数目的增多，对偶间隙减小。两点有共通之处。需要指出的是，无论是充电控制还是充放电控制，收敛过程中均有的一定的振荡，这有待进一步研究、改进。

图2 算法的迭代过程Fig.2 Iterative procedure of proposed method

5 结论

电动汽车数量众多、约束复杂，这决定其充放电控制必须通过分布式机制实现；本文对分布式控制机制进行了总结。针对已有方法的局限性，本文提出了一种基于LR的分布式机制，降低系统发电成本。该方法具有以下优势：实现电动汽车间协调运行的同时，实现了电动汽车与发电机组的协调运行；降低了发电成本，提升了系统运行的经济性；可以处理约束耦合、目标函数非凸的其他类型的充放电控制问题，适用范围更广；对大规模电动汽车群适用性较强。

本文所提出的方法适用于其他类型或可控负荷，可为负荷调度的实现提供思路。但本文尚未涉及电动汽车与可再生能源电力的协调运行，也未考虑电力系统网架约束，这些问题有待进一步研究、完善。