数据拟合在可燃气体报警器检测中的应用

金元庆

（福建省三明市计量所，三明 365000）

0 引言

可燃气体的爆炸下限是指可燃蒸汽、气体或粉尘与空气组成的混合物遇火源即能发生爆炸的最低体积分数，用%LEL表示。在相关的国家标准（如GB 15322 系列国标）中，也都使用LEL的百分数来设定可燃气体的危险程度指标，气体报警器的生产厂家和用户一般也将其报警上、下限设置为50%LEL和25%LEL左右，此即思味着，不论何时，一旦可燃气体浓度超过设定值，就存在产生燃烧并引发危险的可能性。然而，各种可燃气体的爆炸极限实际上都不是一个绝对和固定的值，它受到多种环境因素的影响，人们也很难在生产和工作现场准确判定可燃可爆气体的安全浓度范围。当环境条件发生改变时，如工作现场温度及气压的明显增加，或空气中氧气浓度显著富余的情况下，都会使气体的燃烧爆炸限范围发生明显改变，从而增加检测工作过程的危险性。因此，在国家计量检定规程《可燃气体检测报警器》中，将仪器示值误差检测点的浓度值分别设定为仪器满量程的10%，40%，60%。其检测最高浓度远低于相应气体的爆炸下限和仪器的满量程示值，相关的国家标准也明确规定了隔爆型气体检测器不得在超过规定的浓度范围使用。

然而，上述气体浓度示值点的检测往往不能满足一些客户的实际要求和其工作需要，在很多场合，人们必须了解可燃气体检测仪器在较高浓度下的工作情况和实际误差值。，在许多计量检测过程中，测量的目的往往不只是要求获得一个或几个被测量的示值，更重要的在于了解相关被测仪器输人量和输出量的某种对应关系，确定它们的变化趋势和响应特性，比如各种校准和定标曲线及特性曲线的测量等。因此，本文试图通过对低浓度下可燃气体报警器有限的检测数据进行拟合分析，以获得高浓度下气体报警器的实际工作情况和相应的测量误差值。

1 方法简介

从可燃气体报警器的工作原理可知，被测气体浓度值与仪器的响应电参量值之间有很强的相关关系。以低浓度下的一组测量数据为样本观测值，用最小二乘法的数据拟合技术来确定气体浓度与仪器测量值两个变量之间的回归函数关系式y＝f（x），并将经过检验的回归模型用于分析预测高浓度情况下可燃气体报警器的响应特性和实际误差值，从而避免可燃气体报警器在爆炸限浓度范围内检测时可能带来的危险性。

2 收集、整理统计数据

回归分析就是根据实际检测所得的数据来建立数学模型，并进行数据分析。以低浓度下检测所得的一组测量数据作为回归变量的样本统计数据，因此收集、整理检测数据是建立回归模型的重要环节和一项基础性工作。样本数据的质量，对所建模型的精度有至关重要的影响。下面首先从样本检测数据的采集出发，阐述如何建立可燃气体报警器的回归预测模型。

选择一台性能稳定，灵敏度高，一致性好的可燃气体报警器作为被测对象（如有必要，可预先在洁净空气中对报警器进行调零标定或设置），然后，根据检定规程的检定条件和检定方法，依次通人不同浓度的标准气体对被测仪器进行实际测量，记录不同气体浓度下仪器相应指示（响应）值。这里将输人气体的浓度值记为xi，相应的仪器响应值记为yi，则x、y即为所要讨论的两个具有某种相关关系的变量，回归分析就是要从上述所记录的一组测量数据（x1，y1），（x2，y2），…（xn，yn）中，用统计分析方法找出某种相依关系的数学表达式y＝f（x）。由于（xi，yi）是由实验通过观察测量所得，往往都带有随机误差。因此，为了减弱或消除这些误差影响，提高数据拟合的准确度，除了要严格按规程规定的条件进行测量外，实际操作过程中应适当增加不同浓度检测点（可采用气体稀释标准装置配置不同浓度的标气），并对同一浓度示值点进行重复多次测量，将求得的平均值代替每个yi值，这样就可根据这些实测数据来求解模型的各个参数，减小分析系数α 和β 估值的标准偏差，提高数学模型的拟合精度。

3 确定回归模型

回归模型的建立是基于回归变量的样本统计数据，通过将实验所得的一组测量数据归纳总结为经验公式，并将其做进一步的推演分析和应用。以上述可燃气体报警器检测过程收集、整理的一组数据为样本观测值（xi，yi），通过数学方法，研究气体浓度和仪器响应值两个变量间的统计关系或相关关系。首先在坐标轴上按实测数据画出散点图（xi，yi），也即将变量系列的测量数据显示为一组点，变量值由各点在图表中的位置表示，这样就可通过观察这组数据在坐标系上的分布情况，直观判断两个变量之间存在何种相关关系，从而确定选择哪种函数类型进行拟合。表1 中的数据点列（xi，yi）是通过上述步骤所测的一组数据，相应的数据散点图如图1 所示。图1 表明，这些点大体分布在一条直线附近，具有线性分布特征和变化趋势，因此，可采用线性回归分析方法，通过这些坐标点做出一条足以表示y与x之间真正关系的直线y＝α +βx。这里最便捷的处理方法就是利用Excel的回归函数和图表向导功能，通过以下步骤快速实现对“散点图”（xi，yi）的绘制、回归模型估计及回归分析系数α 和β 值的计算。

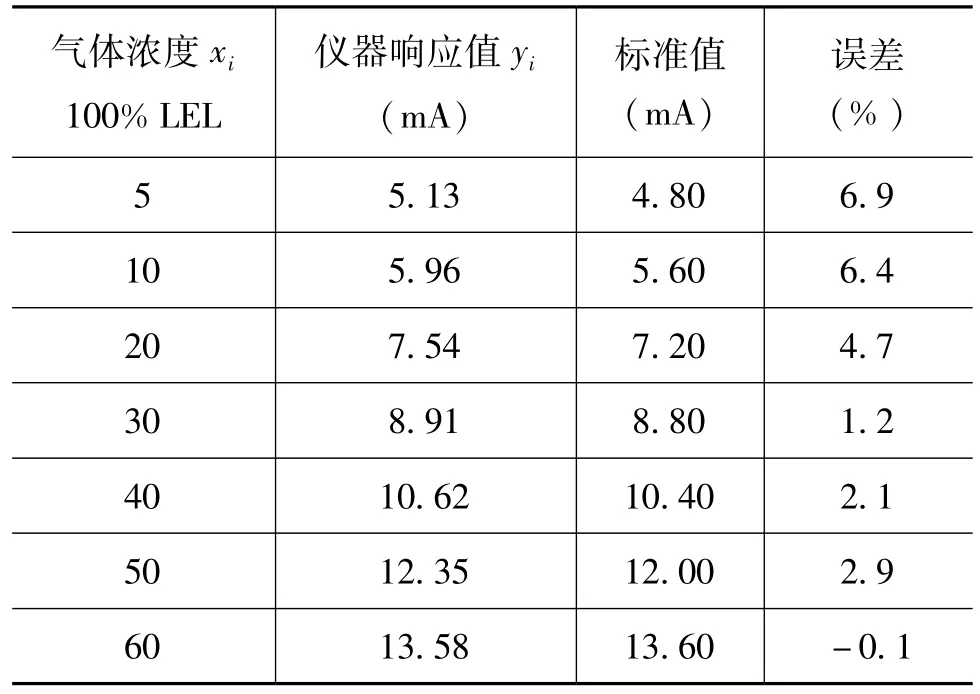
表1 实测数据表

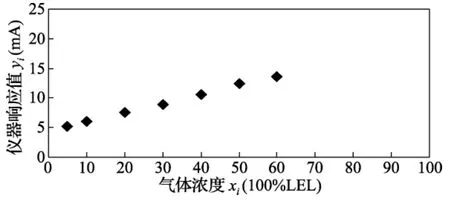
图1 散点图

1）在Excel中选择表1 数据点列（xi，yi）；

2）选择“图表类型”为“散点图”；

3）选择“分析类型”为“线性（L）”；

4）选中“显示公式（E）”和“显示R平方值（R）”；

5）确定，即得回归结果，图2 所示。

图2 中还给出了回归模型相应的判定系数R2，这样就初步确定了所需要的回归模型。当该回归模型经过检验后就可用于分析预测高浓度情况下可燃气体报警器的响应值，表2 为利用该线性回归模型进行预测所得的一组预测数据及其误差值。

图2 回归模型

表2 预测数据

上述是我们常见到的可燃气体报警器仪器响应特性和回归模型类型，它们在一定使用范围内呈线性关系，有些仪器则通过测量线路的某些补偿措施，设计成近似的线性关系。但由于气敏传感器的种类较多，测量原理各异，它们对各种可燃气体浓度的响应特性和灵敏度也各不相同，反映在回归模型上就不一定呈线性相关关系。例如，在可燃气体报警器中应用较多的电阻式半导体气敏传感器。其作用机理是，半导体气敏器件同被测气体接触后，器件表面产生吸附作用引起电阻值的变化，使测量电路的电桥失去平衡，产生电压输出（有的仪器是根据测量线路中负载取样电阻电压降的变化），从而将不同气体浓度值变换成与其相关的电信号。但这种相关关系多数情况下呈非线性函数关系，如对数、指数、幂函数或二阶多项式等。对非线性模型，同样可以利用上述方法进行回归预测。实际操作过程中，由于观测的样本数据量有限，当从数据散点图无法直观判定属于何种类型的回归模型时，可先通过上述方法分别选择几种可能的非线性分析类型，利用Excel图表功能快速建立相应的数学模型，然后，从图表上直观比较并寻找拟合效果最好、精度最高的类型。表3 是该类型报警器的一组实测数据，图3 是该组数据对应的几种非线性拟合模型的比较图。图中分别列出了几种非线性拟合模型的数学关系式和它们的拟合优度R2。从中可方便判别出拟合精度最高的回归模型为幂函数关系，其函数关系式为：

图3 非线性拟合模型比较图

表3 实测数据

通过变换成对数形式，该气体报警器拟合模型为：

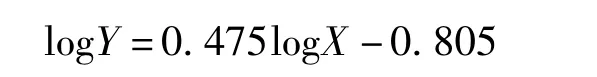
式中，Y为气体传感器输出电压测量值（V）；X为被测气体浓度值（100%LEL），系数（0.475 和-0.805）则是由传感器元件、测量气体种类、测量温度、湿度及报警器测量电路工作电压大小等因数决定。对于某一特定的气体报警器而言，在规定的测量条件下，可看作是固定值。

4 回归模型验证

建立回归模型的目的就是为了应用模型进行分析预测，然而，单纯通过数量关系所建立的回归模型是否合理，能否用于实际的预测分析，将取决于对该模型进一步的检验分析和对预测误差的计算，比如相关性及显著性水平的计算验证等。回归模型只有通过各种检验，且预测误差较小，才能够根据该模型作进一步的预测。表2 中给出了利用上述线性回归模型进行预测所得的一组预测数据及其误差值，其预测准确度能够满足实际测量要求。

我们也可以通过判定系数R2来判定回归模型方程拟合的效果如何，R2越大说明回归模型拟合的越好（R2的取值范围为[0，1]）。图2 和图3 中已给出各种回归模型相应的R2值，我们也可根据Excel函数RSQ（）直接计算判定系数，即拟合优度R2，将上述测量数据（表1）输人公式RSQ（）中，可得到判定系数R2＝0.9987，结果显示由表1 实验数据所得的回归公式能够解析99%以上的实验数据，说明该回归模型整体的拟合效果良好。而图3 中可由判定系数R2最大值直接判定拟合精度最高的非线性回归模型。

5 结论

通过上述预测结果的误差计算和预测模型的检验分析，结果表明，利用最小二乘法的数据拟合技术所建立可燃气体报警器的回归估计模型，能很好的拟合实测数据，该预测方法的可靠性较高，简便、经济、易操作，预测精度能够满足实际检测工作需要，对各类气体报警器包括有毒气体的实际检测工作，都具有一定的参考价值。